4.3. Парамагнитный ион в кристаллическом поле

П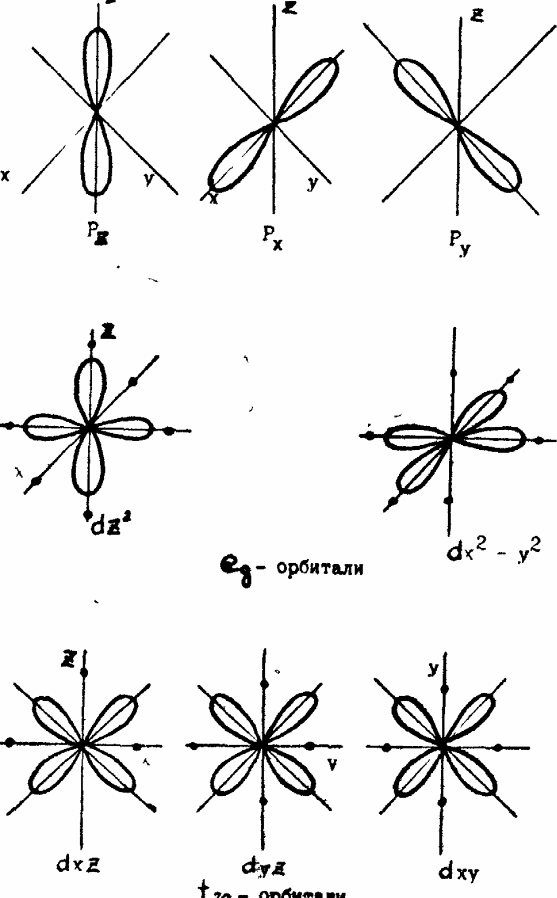 режде чем перейти к коллективным явлениям (ферромагнетизм, антифер- ромагнетизм и др.), рассмотрим как действует

Рис. 4.6. Волновые функции Р и d -электронов.

Заметное влияние оказывает поле лигандов на d –электроны. Для редкозе- мельных ионов эффект влияния значительно слабее, так как электроны 4f обо- лочки (обуславливающие магнитный момент экранированы от поля лигандов внешними электронами 5S, 5P, 5d, 6S –оболочек) на отдельный парамагнитный ион его окружение в кристалле. Электроны внутренних слоев оболочки атома экранированы от воздействия других атомов или ионов в кристалле внешними электронами, поэтому они ощущают влияние атомов окружения слабо (явление поляризации). Поэтому внутренние электроны остаются локализованными, и их состояние мало отличается от состояния в свободном атоме. Представим, что положительный парамагнитный ион окружен диамагнитными отрицательными ионами (такие ионы называют лигандами; поле, создаваемое этими ионами - лигандами - полем лигандов). Это внутрикристаллическое поле оказывает дей-

ствие на орбитальный и спиновый моменты иона, следовательно, состояние ио- на зависит от симметрии этого поля и его напряженности.

Лиганды, окружающие данный парамагнитный ион, создают большие куло- новские поля, которые влияют на внешние электроны и приводят к расщепле- нию их состояний.

Рассмотрим влияние поля кубической симметрии на состояние ионов. Вол- новые функции р и d -орбиталей приведены на рис.4.6. На P-состояния, волно- вые функции которых имеют вид гантели, кубическое поле не оказывает влия- ния, и Р- уровни имеют одинаковую энергию.

Заметное влияние оказывает поле лигандов на d -электроны. Для редкозе- мельных ионов эффект влияния значительно слабее, так как электроны 4f обо- лочки (обуславливающие магнитный момент) экранированы от поля лигандов внешними электронами 5S-,5p-^-,5d-,6S-оболочек.

Для d-электронов существует два типа волновых функций (см. рис.4.7), кото- рые называются t_2q -орбиталями. Имеется 3t- орбитали, распределение элек- тронной плотности которых имеет вид розетки, лепестки которой имеют ось симметрии, расположенной под углом 45° к осям координат; и 2l_q орбитали, ле- пестки розетки которых совпадают с осями координат.

Предположим, что парамагнитный ион расположен в центре куба и окружен

6-ю диамагнитными ионами (рис.4.7). Поле лигандов в этом случае приводит к тому, что 2J+1 возможных электрических состояний, ранее вырожденные (квантовые уровни соответствующие одинаковой энергии), расщепляются на две группы (рис. 4.8), причем более низкую энергию из-за электростатического отталкивания зарядов будет иметь триплетный уровень t_2q (в поле кубической симметрии функции dxy, dyz,dxz эквивалентны и энергетически вырождены), а

б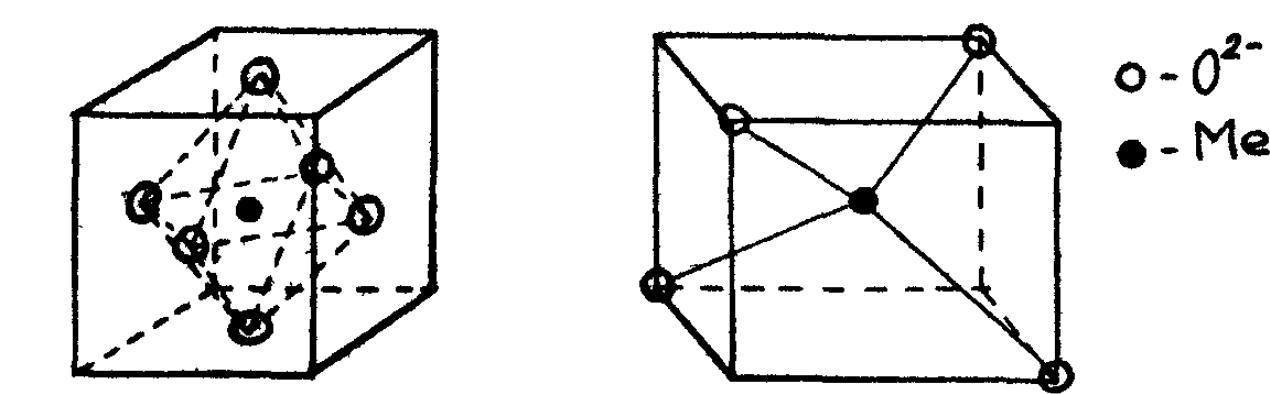 олее высокую - дуплет _q.

Рис. 4.7. Парамагнитные ионы в октаэдрическом и тетраэдрическом окруже- ниях диамагнитных ионов, О^2-

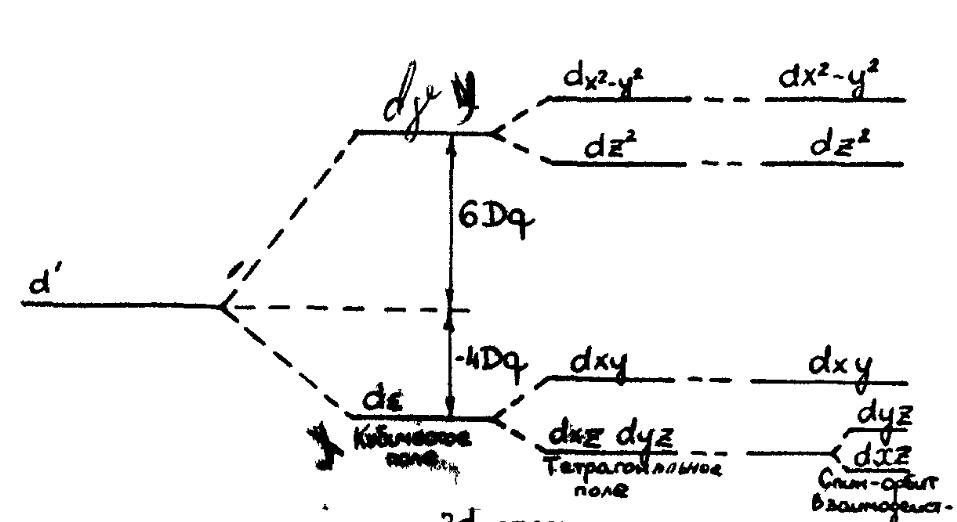
Рис. 4.8. Расщепление 3d-уровня в кристаллическом поле

В тетраэдрическом а также кубическом, додекаэдрическом окружениях, по- следовательность уровней сменится обратной. Величина расщепления обозна- чается символом  или 10Д_q и является основной величиной, определяющей расщепление в поле кубической симметрии. Величина  зависит от вида катио- на, конфигурации поля лигандов и заряда лиганда.

Относительное положение уровней l_q и t_2q в кубическом поле можно охарак- теризовать с помощью параметра . Обозначим для одного d-электрона вели- чину энергии уровня t_2q через X, а уровня l_2q– через Y.

Примем энергию нерасщепленного уровня равной нулю, тогда получим

3X  2Y  0 . (4.30)

Используя определение параметра расщепления

_{| Y - X |  ,} (4.31)

получим, что

^{|Y|=3/5=6Д}_q^{, |Y|=2/5=4Д}_{q. (4.32)}

Октаэдрическая и тетраэдрическая конфигурации встречаются практически во всех ферримагнитных кристаллах и представляет в нашем случае наиболь- ший интерес.

Если поле лигандов имеет компоненту более низкой симметрии, чем кубиче- ское, то происходит дальнейшее расщепление уровней t_2q и l_q. Эти компоненты могут снять большую часть орбитального вырождения.

Из рис. 4.8 видно, что в кристаллическом поле основному состоянию иона соответствует более низкая энергия, чем свободному иону. Разность энергии свободного иона и иона, испытывающего влияние кристаллического поля, на-

зывается энергией стабилизации E_c в кристаллическом поле. Для одного d- электрона энергия стабилизации определяется непосредственно положением t_2q (d)- уровня в октаэдрическом поле и l_q(d) - уровня в тетраэдрическом поле. В соответствии с (4.32) энергия стабилизации в октаэдрическом поле E_c=6Д_q, а в тетраэдрическом поле E_c=6Д_q.

В случае большего числа электронов энергию стабилизации можно опреде- лить, зная заселенность уровней t_2q и l_q. Если энергия свободного иона равна нулю и заселенности уровней n_t и n_e, то энергия стабилизации

^Е_с ^{ -(n} _t ^E _t ^{ n} _e ^E_e ^{) .} (4.34)

Энергия стабилизации является одним из факторов, определяющих катион- ное распределение ионов по различным позициям (октаэдрическая, тетраэдри- ческая) в структуре окисных соединений (ферритов и др).

Для того чтобы решить, какая из конфигураций оказывается предпочтитель- нее для того или иного иона, нужно сравнить значения энергии стабилизации E_t и E_e, определяемые параметром расщепления . Величину , как правило, оп- ределяют экспериментально по оптическим и инфракрасным спектрам погло- щения.

Величина потенциала кристаллического поля оказывает существенное влия- ние на состояние ионов в кристалле. Взаимодействие внешних локализованных электронов в кристалле можно охарактеризовать добавлением к гамильтониану свободного иона соответствующих членов.

Гамильтониан для электронов парамагнитного иона в кристалле можно запи-

_{сать в виде:}

_{€ € €}

^{H  H} _O ^{ V}_L ^{ V}_ij ^{ H} _LS ^{ V}_kn ^{. (4.35)}

Первые четыре члена выражения соответствуют гамильтониану свободного иона. Гамильтониан Н₀ равен сумме одноэлектронных вкладов в энергию от

всех внешних электронов иона:

_{O }

_p ²

_{H  (} ⁱ _

^2m

_{Z эффe}

2

_{) ,}

^r_i

в этом случае

p ²   ²  ² - оператор квадрата импульса электрона; m, e - его заряд

и масса; Ze – заряд ядра.

V

^{Член €}_L

(уравнения (4.35)) характеризует взаимодействие электронов с

^{ядром, V€}_ij

- электростатическое взаимодействие между электронами, H_LS - спин-

орбитальное взаимодействие.

В зависимости от относительной величины чая интенсивности кристаллического поля:

ij

V^€ , H_LS и

V

^€_kn различают три слу-

1) слабое кристаллическое поле (радиоземельные ионы) -

^{2) промежуточное поле (3d -ионы) –H}_LS^<V_kn^<<V_ij^;

kn

V^€ <H_LS;

3) сильное кристаллическое поле (4d ,5d -ионы) V_kn>V_ij>H_LS.

В случае слабого кристаллического поля состояние иона характеризуется квантовым числом J. В этом случае спин-орбитальное взаимодействие и муль- типлетная структура сохраняются.

Промежуточное поле, характерное для ионов с 3d внешними электронами, разрушает спин-орбитальную связь; числом J уже нельзя характеризовать со- стояние иона, но квантовые числа L и S сохраняют еще свой смысл. Случай сильного поля встречается для 4d и 5d -электронов (в отдельных случаях и для

3d -электронов). Сильное кристаллическое поле нарушает взаимодействие ме- жду электронами, и вместо квантовых чисел L и S состояние характеризуется заселенностью орбиталей t_2q и l_q. Так, например, в сильном октаэдрическом по- ле заполняются сначала t_2q –орбитали, и только после этого орбитали l_q . При-

_{чиной этого оказывается сильное взаимодействие диамагнитных ионов окру-}

_{2 2 2}

^{жения с орбиталями d}_Z

^{и d}_X ^-_Y

, которые оказываются невыгодными для раз-

мещения на них d-электронов; правила Хунда при этом оказываются неприме- няемыми. На рис.4.9 приведены картины заполнения электронами t_2q и l_q - ор- биталей в случае промежуточного и сильного октаэдрического полей для элек- тронных конфигураций d² и d⁵ .

Из рис.4.9 видно, что под действием сильного кристаллического поля возмо- жен переход из одного спинового состояния в другое; например, для электрон- ной конфигурации d⁵ возможен переход из высокоспинового состояния S=5/2 в низкоспиновое S=1/2. Экспериментально такие переходы наблюдались для конфигураций d⁴ , d⁵ ,d⁶ и d⁷.

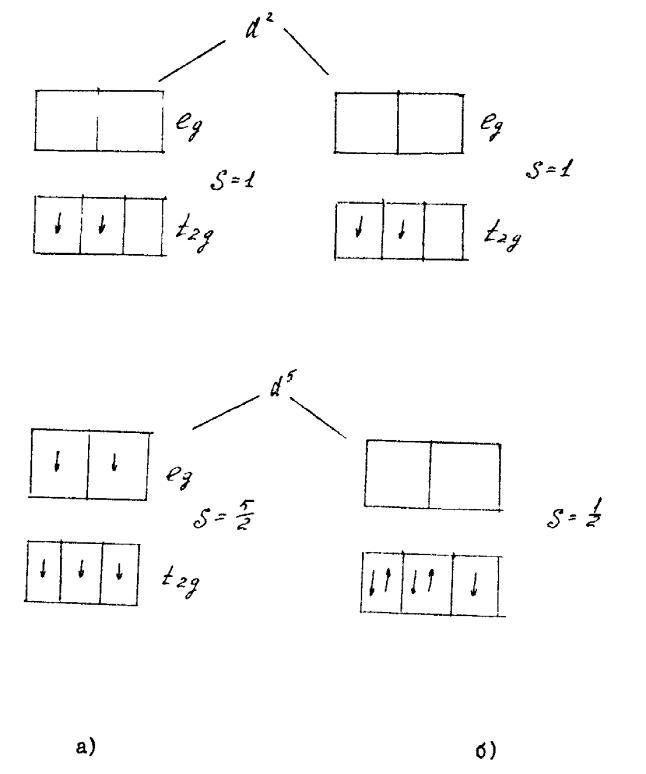
Рис.4.9. Заполнение электронами t_2q и l_q -орбиталей в случае промежуточного

(а) и сильного полей (б) для конфигурации d² и d⁵

Остановимся еще на одном важном эффекте влияния кристаллического поля на ионы - "замораживании" орбитального магнитного момента ионов. Выше было показано, что орбитальное вырождение свободного атома связано с вели- чиной квантового числа L, которое определяет кратность вырождения 2L+1. Внутрикристаллическое поле снимает орбитальное вырождение частично или полностью, при этом расстояние между расщепившимися уровнями может быть значительным, и при нормальных температурах занят только наинизший уровень. Если спин-орбитальное взаимодействие мало, то орбитальный момент оказывается замороженным.

Кристаллическое поле с низкой симметрией приводит к изменению орби- тального момента электронов, орбиты меняют свое направление в пространст- ве, меняется и проекция L_Z , при этом могут произойти такие изменения орби- тального движения, что среднее значение проекции орбитального момента на ось Z становится равным нулю <L>=0. В этом случае мы говорим о заморажи- вании орбитального момента количества движения, а следовательно, орбиталь- ного магнитного момента.

В случае октаэдрической конфигурации не обладают орбитальным вырожде- нием ионы с конфигурацией 3d³, 3d⁸ и 3d⁵ , последняя конфигурация и для сво-

бодного иона имеет состояние ⁶S (орбитальный синглет), в котором орбиталь- ный момент равен нулю. Основным состоянием ионов d⁴ и d⁹ является дублет, но и у этих ионов орбитальный момент заморожен, т.е. среднее значение L_Z=0. В кристаллическом поле кубической симметрии (октаэдр) только для ионов с конфигурациями 3d¹, 3d² , 3d⁶ и 3d⁷ обладающих трехкратным орбитальным вы- рождением, орбитальный момент не является замороженным. Сильное спин- орбитальное взаимодействие может приводить к частичному размораживанию орбитального момента, т.е. это взаимодействие действует противоположно кри- сталлическому полю. В сильном кристаллическом поле, как показано выше, для

октаэдрического поля происходит заполнение электронами уровня t_2q, вплоть до максимально возможного числа t⁶_2q, и только после этого начиная с d⁷ и за-

полняется уровень. Этот эффект называют "замораживанием" спина.