Парамагнетизм
Парамагнетизм- это свойство вещества, состоящего из отдельных и независимых диполей, намагничиваться, если данное вещество внести в магнитное поле, которое сообщено внешним источником.
Если внести любое вещество в магнитное поле, то под его действием вещество приобретает магнитный момент m , который для не слишком сильных полей можно записать:
|
,где Н - напряженность магнитного поля;
- магнитная восприимчивость.
Парамагнетики - это такие вещества, у которых >0, парамагнитная восприимчивость n, значительно больше диамагнитной 0. К парамагнитным веществам относятся и чистые металлы, в которых спины электронов проводимости, могут слабо упорядочиваться под действием магнитного поля. Парамагнетизм в этом случае незначителен, а так как на электроны проводимости тепловое движение не оказывает большого влияния, то намагниченность практически не зависит от температуры. Однако существуют вещества, которые обнаруживают сильные парамагнитные свойства, обусловленные существованием в атомах или молекулах постоянных магнитных моментов электронов с неспаренными спинами, например: EuSiO3, FeNH4(SO4)212H2O, KCr(SO4)212H2O, Cd2(SO4)38H2O, Cd2O3 и др. В этих веществах расстояние между магнитно-активными ионами достаточно велико, и взаимодействие между ними практически отсутствует.
Вследствие теплового движения магнитные моменты отдельных атомов или ионов ориентируются случайным образом. Если такую систему поместить во внешнее магнитное поле, то магнитные моменты атомов или ионов будут стремиться ориентироваться вдоль поля, в результате чего система приобретает результирующую намагниченность.
Свойство системы отдельно независимых диполей намагничиваться во внешнем магнитном поле называется парамагнетизмом.
Существует несколько теорий, которые рассматривают поведение парамагнетика во внешнем поле. При рассмотрении физики этого процесса, большую роль играют не только напряженность магнитного поля, но также температура. Впервые данную проблему рассмотрел в 1905 году Ланжевен и создал свою теорию, которая называется классической теорией парамагнетизма Ланжевена. Но она в состоянии лишь приблизительно описать поведение материала в поле. Более точно его описывает квантовая теория, которая основана, на квантовой природе магнитного и механического момента атома.
Классическая теория парамагнетизма Ланжевена
Рассмотрим находящийся в тепловом равновесии совокупность магнитных частиц, помещенных в магнитное поле напряженностью Н. Если предположить, что магнитные и электростатические взаимодействия между ними отсутствуют, («идеальный» парамагнитный газ), то на ориентацию диполей будет влиять лишь внешнее магнитное поле, стремящееся ориентировать магнитные диполи по полю, и тепловое движение частиц, которое стремится разрушить эту ориентацию.
Дезориентация частиц за счет теплового движения не будет полной, т.е. всегда сохраняется какая-то степень упорядочения, в результате чего появится магнитный момент системы (поляризационная намагниченность), причем вектор намагниченности будет совпадать с направлением Н. Намагниченность системы М может быть оценена при помощи закона канонического распределения Максвелла - Больцмана. Этот закон сводится к следующему утверждению: вероятность того, что данная частица, находящаяся в тепловом равновесии с другими частицами, будет обладать энергией En, - пропорциональна e-En/kT, т.е.,
|
,где С- постоянная пропорциональности
e-En/kT – множитель Больцмана;
En – потенциальная энергия частицы во внешнем поле;
k - постоянная Больцмана.
Потенциальная энергии En может быть записана
|
,где - магнитный момент диполя;
- угол между векторами и Н.
Ланжевен предположил, что магнитные моменты ориентируются под любым углом к внешнему полю, но преимущественные направления моментов должны находиться под углами в диапазоне 0.
Для того чтобы определить намагниченность системы, помещенной в магнитное поле, представим в этой системе сферу радиусом r=1 и выделим в этой сфере телесный угол d:
|
.Число ориентированных частиц в телесном углу по статистике Максвелла-Больцмана запишем
|
.Подставим значения En и d
|
.Обозначим через а=Н/kТ и найдем полное количество одинаково ориентированных частиц n по всем углам
|
.Очевидно, что магнитный момент парамагнитного вещества определяется компонентами, параллельными магнитному полю, так как компоненты всех частиц, перпендикулярные внешнему полю, из соображений симметрии взаимно компенсируются. Тогда намагниченность вещества
|
.Подставив в (4.8) выражение для С из (4.7) и проведя замену пределов интегрирования, получим окончательное выражение для М:
|
.Решение этого уравнения дает
|
.Величина, заключенная в скобки, есть выражение функции Ланжевена L(a)
|
.Поэтому можно записать
|
|
,Где М0=N - магнитный момент системы Т=0 К, т.е. когда все диполи, имеют одинаковую ориентацию. Предельные значения функции Ланжевена L(0)=0 и L()=1. Отсюда вытекает следующее физическое следствие при слабых внешних полях М0 и высоких температурах: при малых значениях аргумента функции Ланжевена cth a можно разложить в ряд
|
|
.В силу малой величины аргумента а можно ограничиться лишь двумя первыми членами ряда. Тогда
|
|
.Подставим это значение в уравнение (4.10):
|
|
.Отсюда для восприимчивости парамагнетика находим
|
|
.Обозначив через C=2N/k, получим аналитическое выражение закона Кюри:
|
|
.Этот закон утверждает, что магнитная восприимчивость при слабых внешних полях и высоких температурах изменяется обратно пропорционально температуре. Графически закон Кюри представлен на рис
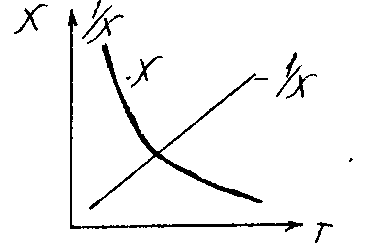
Рис Зависимость восприимчивости парамагнетика и ее обратной величины от температуры
В другом предельном случае при сильных полях и низких температурах функция Ланжевена L(a)1, а намагниченность асимптотически приближается к M0.
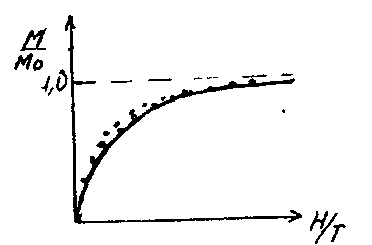
Рис Зависимость относительной намагниченности парамагнетика от обратной температуры.
На рис показана зависимость M/M0 от величины H/T. Сплошной линией показана теоретическая зависимость, точками обозначены экспериментальные значения. Видно, что изменение намагниченности качественно описывает поведение парамагнетика. Экспериментальные значения не совпадают с кривой.
Значительно лучшие результаты дает применение квантовой теории.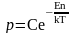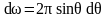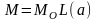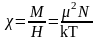