2. Понятие о функциях и операторах.

Важным понятием системы Maple является понятие функции. Функция возвращает результат некоторого преобразования исходных данных – параметров функции по определенному правилу. Maple имеет множество встроенных функций, включенных в его ядро и в пакеты.

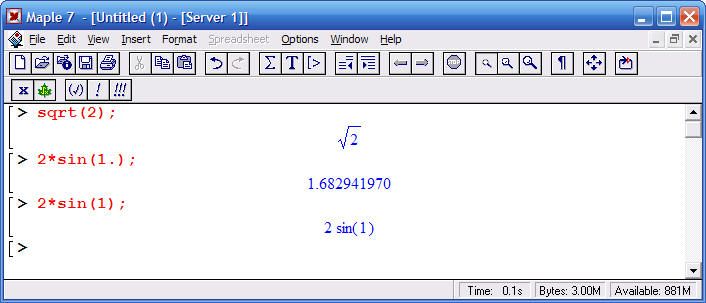
Функция в выражениях задается вводом ее имени и списка параметров функции (одного или нескольких), заключенных в круглые скобки: например, sqrt(2) задает функцию вычисления квадратного корня с параметром 2 (численной константой). Основным признаком функции является возврат значения в ответ на обращение к ней по имени с указанием списка параметров этой функции.

Обратите внимание на особую роль десятичной точки – здесь она служит указанием к выполнению вычисления значения sin(1.0). А вот синус целочисленного аргумента 1 не вычисляется – считается, что вычисленное значение менее ценно, чем точное значение sin(1).

Помимо функций, в математических системах для записи математических выражений используются специальные знаки – операторы. К примеру, вычисление корня квадратного часто записывается с помощью его специального знака - √. Какие еще бывают операторы: операторы сложения – «+», вычитания – «-», умножения – «*», деления – «/» и другие. Пожалуй, самым распространенным оператором является оператор присваивания :=. Он используется для задания переменным конкретных значений, например:

Другой распространенный оператор – оператор равенства = используется для задания равенств и логических условий (например, a=b)

либо указания областей изменения переменных (например, x=-15..15)

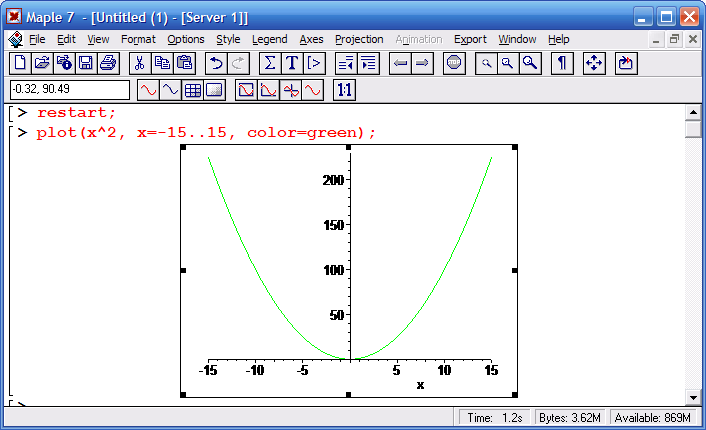
также оператор равенства используется для определения значений параметров в функциях и командах (например, color=green для задания зеленого цвета у линий графиков)

Операторы сами по себе результат не возвращают. Но они позволяют конструировать математические выражения.

Я уже упоминала важность точки для получения численного значения какого-либо вычисления. Пример с sin(1) и sqrt(2). Но получить целочисленное значение можно, воспользовавшись функцией evalf ().

Обратите внимания, что появился новый оператор – %, который применятся для исполнения предшествующего действия.

Нюанс: Результат точных целочисленных операций Maple стремится представить в виде рационного числа – отношения двух целых чисел:

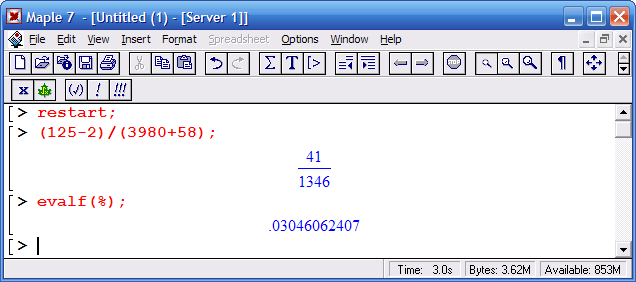
Для вывода на экран используется оператор «точка с запятой», а для блокирования вывода оператор «двоеточие»

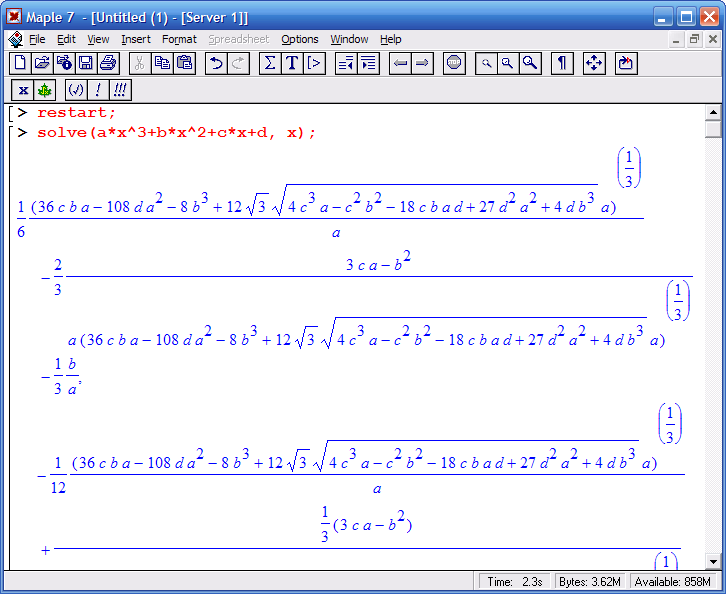
Что еще можно сказать про операторы: некоторые операторы могут записываться в виде инвертных функций, которые выводят записываемое выражение, но без их исполнения. Такие функции обычно записываются с большой буквы:

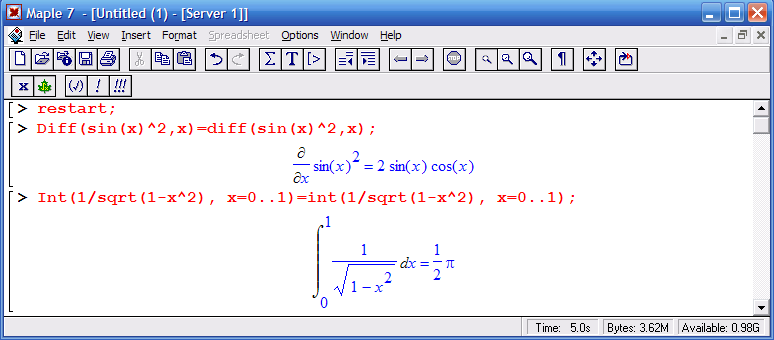
Этот пример как раз и иллюстрирует применение функции интегрирования – обычной int и инвертной Int.

В первом случае Maple вычисляет интеграл предельно точно и дает ответ в виде рационального числа. Во втором примере просто выводит запись интеграла в математической нотации. В третьем случае функция evalf вычисляет этот интеграл и возвращает результат уже в форме числа с плавающей точкой.

Примеры задания функции пользователя и построения ее графика.

Символьные вычисления

Maple открывает обширные возможности выполнения символьных (аналитических) вычислений. Начнем с простого примера – требуется найти сопротивление трех параллельно включенных резисторов R₁, R₂ и R₃ произвольной величины. Из курса электротехники известно, что можно задать следующее равенство, определяющее суммарное сопротивление R₀

Дальше, воспользовавшись функцией для решения уравнений solve, можно найти значение R₀ в общем аналитическом виде:

Типовые символьные вычисления

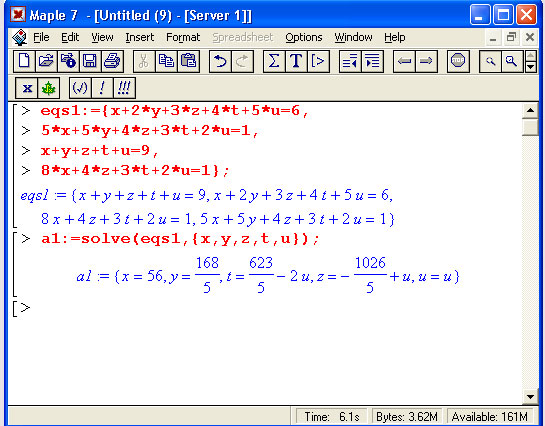
Приведем еще один характерный пример – решение системы линейных уравнений с помощью функции solve. Обратите внимание на форму задания уравнений и выдачи результатов и поразительную естественность решения задачи.

Операции над матрицами

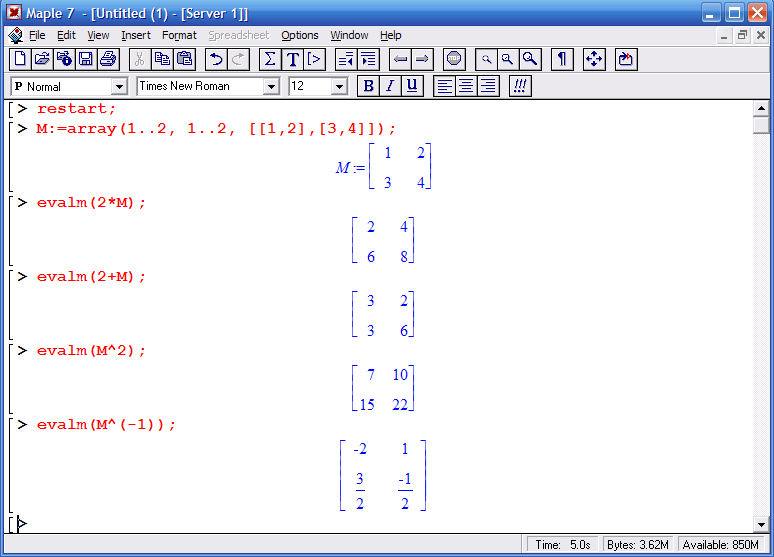
2 способ: подключение пакета linag.

Интерактивный ввод матриц:

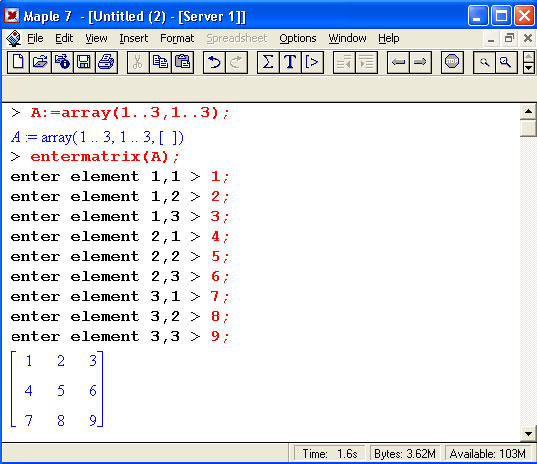
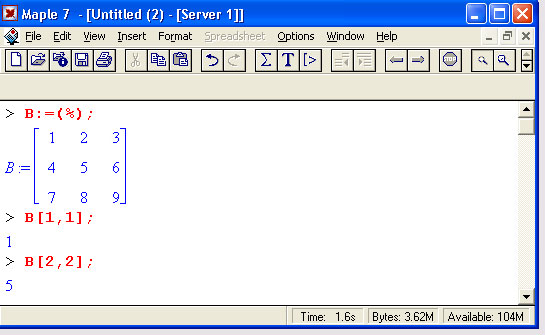
Основные векторные и матричные операции:

Вычисление производных функций f(x)

Для ее реализации Maple 7 имеет следующие основные функции:

diff(a., xl, х2, .... xn) diff(a, [xl, х2, .... хn])

Diff(a, xl, x2, .... xn) Diff(a, [xl, x2, .... хn])

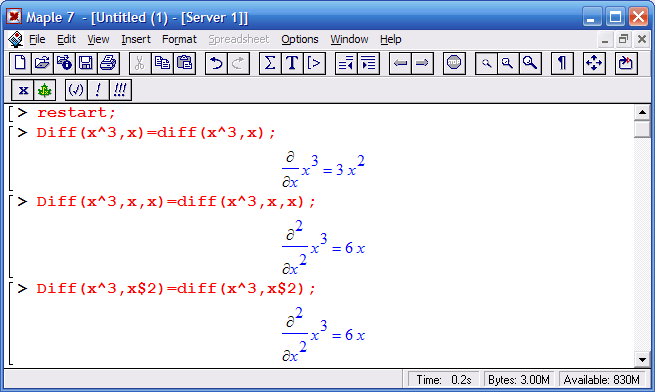
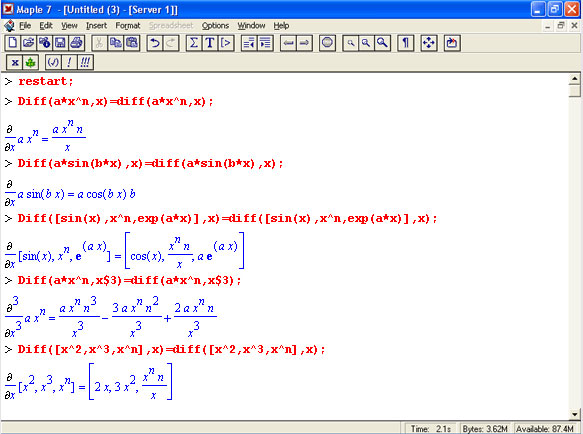
Здесь а – дифференцируемое алгебраическое выражение, властности функция f(xl. x2, .... хn) ряда переменных, по которым производится дифференцирование. Функция Diff является инертной формой вычисляемой функции diff и может использоваться для естественного воспроизведения производных в документах. Первая из этих функций (в вычисляемой и в инертной форме) вычисляет частные производные для выражения а по переменным xl, х2, ..., .хn. В простейшем случае diff(f(x),x) вычисляет первую производную функции f(x) по переменной х. При n, большем 1, вычисления производных выполняются рекурсивно, например diff (f (х), х, у)

эквивалентно diff(diff (f(x), х), у).

Оператор $ можно использовать для вычисления производных высокого порядка. Для этого после имени соответствующей переменной ставится этот оператор и указывается порядок производной. Например, выражение diff (f(x) ,x$4)

вычисляет производную 4-го порядка и эквивалентно записи diff (f (х) ,х,х,х.х). A diff (g(x,y) ,x$2,y$3) эквивалентно diff(g(x,y),x,x.y,y,y) ;

Вычисление неопределенных интегралов

Вычисление неопределенного интеграла обычно заключается в нахождении первообразной функции. Это одна из широко распространенных операций математического анализа.

Для вычисления неопределенных и определенных интегралов Maple предоставляет следующие функции:

int(f,x); int(f,x=a..b); int(f.x=a..b,continuous):

Int(f,x); Int(f,x=a..b): Int(f,x=a..b,continuous):

Здесь f – подынтегральная функция, х – переменная, по которой выполняются вычисления, а и b – нижний и верхний пределы интегрирования

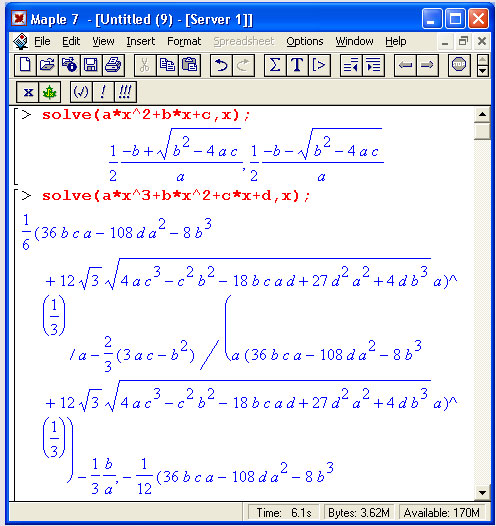
Решение одиночных нелинейных уравнений

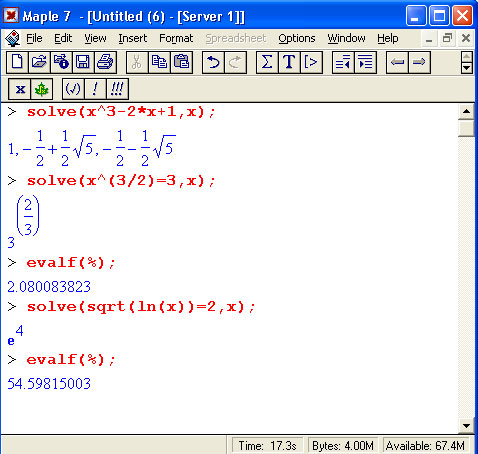
Часто бывает удобно представлять уравнение и его решение в виде отдельных объектов, отождествленных с определенной переменной:

Решение тригонометрических уравнений

Решение неравенств

Неравенства в математике встречаются почти столь же часто, как и равенства. Они вводятся знаками отношений, например: > (больше), < (меньше) и т. д. Решение неравенств существенно расширяет возможности функции solve. При этом неравенства задаются так же, как и равенства. Приведенные на рис. 8.15 примеры поясняют технику решения неравенств.

Из приведенных примеров очевидна форма решений – представлены критические значения аргумента, вплоть до не включаемых значений области действия неравенства (они указываются словом Open). Всегда разумным является построение графика выражения, которое задает неравенство, – это позволяет наглядно убедиться в правильности решения. Приведем еще несколько примеров решения неравенств в аналитической форме:

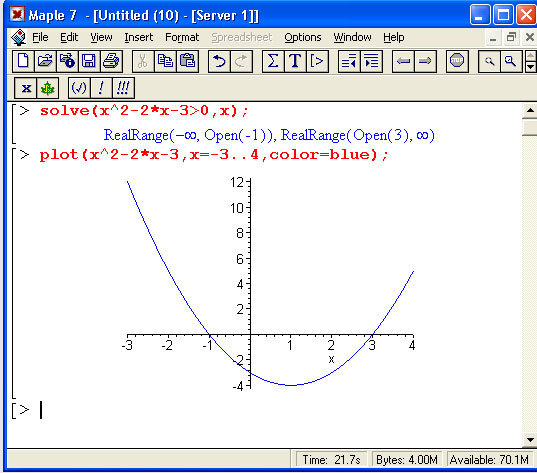
Решение в численном виде – функция fsolve

Для получения численного решения нелинейного уравнения или системы нелинейных уравнений в форме вещественных чисел удобно использовать функцию fsolve

fsolve(eqns, vars);

Решение дифференциальных уравнений.

Дифференциальные уравнения лежат в основе математического моделирования различных, в том числе физических, систем и устройств. Это анализ поведения различных систем во времени (анализ динамики) – полет тела, брошенного под углом к горизонту; вычисление различных полей (тяготения, электрических зарядов).

На следующем слайде представлен раздел справки Maple с классификацией дифференциальных уравнений. В ней представлено:

• 20 дифференциальных уравнений первого порядка;

• 25 дифференциальных уравнений второго порядка;

• 6 типов дифференциальных уравнений высшего порядка

• а также основные функции решения дифференциальных уравнений

Maple позволяет решать одиночные дифференциальные уравнения и системы дифференциальных уравнений как аналитически, так и в численном виде.

Для решения системы простых дифференциальных уравнений (задача Коши) используется функция dsolve в разных формах записи:

dsolve(ODE);

dsolve(ODE, переменная);

dsolve({ODE, нач_услович}, переменная);

Примеры решения дифференциальных уравнений.

Начнем рассмотрение практических примеров с решения простых одинарных обыкновенных дифференциальных уравнения (ОДУ) первого порядка в символьном виде.

Запишем дифференциальное уравнение радиоактивного распада атомов:

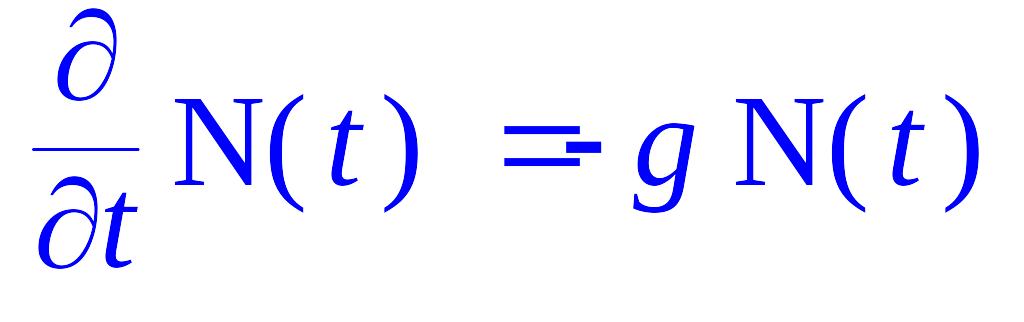
В математическом пакете эта запись имеет вид:

Используя функцию dsolve, получим его общее аналитическое решение:

В решении присутствует произвольная постоянная _С1. Но ее можно заменить на постоянную N(0)=N₀, означающую начальное число атомов в момент времени t=0

Далее можно ввести начальные условия. Например, в начальный момент времени у нас было 100 атомов, а постоянная распада равна 3:

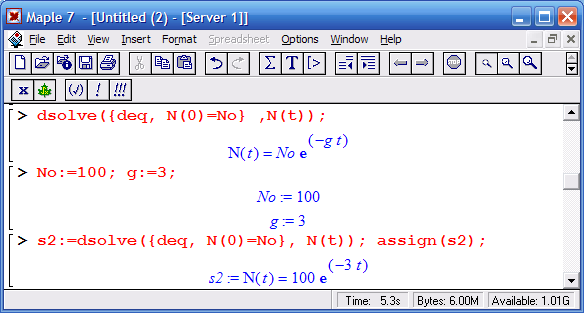
Теперь мы можем воспользоваться полученной зависимостью N(t) и построить график:

график описывает экспоненциальный закон уменьшения числа атомов вещества в ходе его радиоактивного распада.

Другие примеры решения ОДУ первого порядка

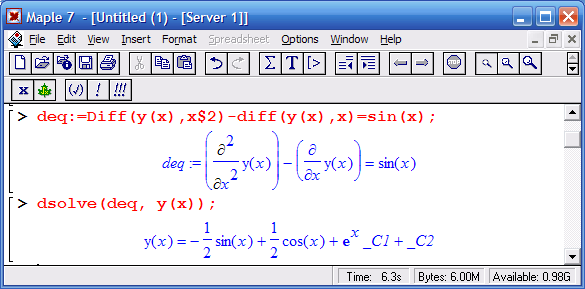
Из приведенного выше примера видно, что для задания производной используется ранее рассмотренная функция diff. С помощью символа $ в ней можно задать производную более высокого порядка.

Рассмотрим физический пример: полет тела, брошенного вверх

Многие физические явления, связанные с движением объектов, в соответствии со вторым законом Ньютона, описываются дифференциальным уравнением второго порядка.

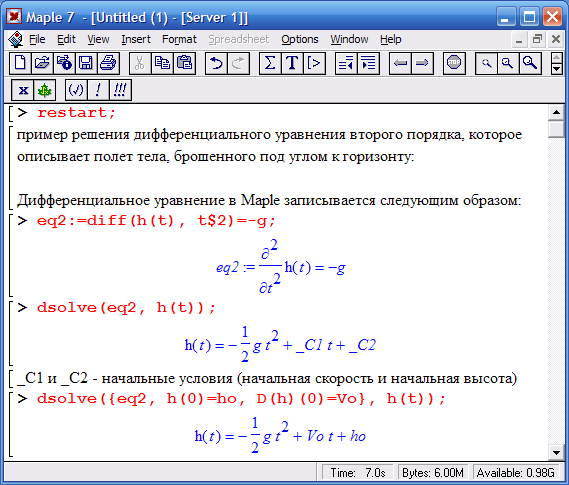
На данном этапе получено общее уравнение для временной зависимости высоты тела h(t). Далее можно подставить конкретные данные и получить график зависимости полета тела от времени.

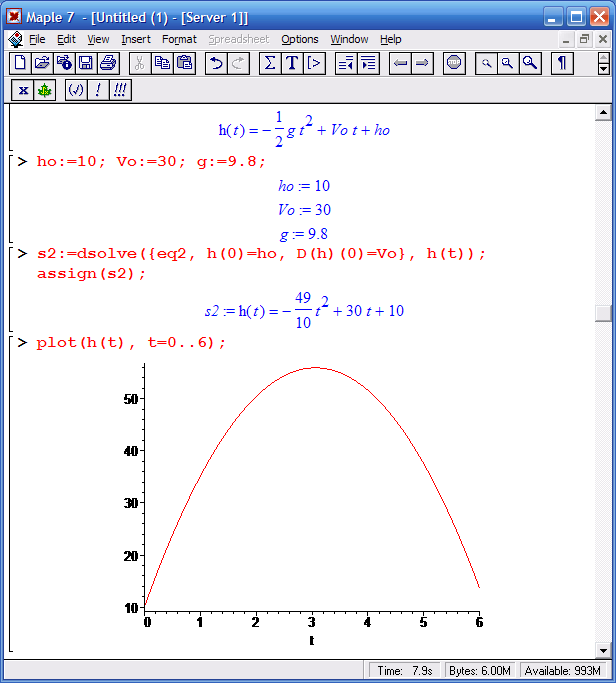
Численное решение дифференциальных уравнений

Большинство нелинейных дифференциальных уравнений не имеет аналитического решения. Кроме того, часто аналитическое решение и не нужно, и достаточно получить результаты в виде графических зависимостей.

В таких случаях для решения дифференциальных уравнений в численном виде используется функция dsolve с параметром numeric.

Рассмотрим тот же пример с полетом тела: