9. Анимация экспериментальных и рассчитанных закономерностей.

10. Минимизация суммы квадратов методом Гаусса-Ньютона. Статистические характеристики оценок параметров модели.

Задача минимизации суммы квадратов методом Гаусса-Ньютона решается путем минимизации целевой функции – остаточной суммы квадратов отклонений измеренных значений координат от рассчитанных по выбранной математической модели при некотором приближении искомых параметров. Минимизация осуществляется путем коррекции начальных приближений параметров. Прием Гаусса-Ньютона заключается в представлении неизвестных решений в виде линейных отрезков многомерных рядов Тейлора по искомым параметрам.

Метод Ньютона-Гаусса — это итерационный численный метод нахождения решения задачи наименьших квадратов. Является разновидностью метода Ньютона. В общих чертах, этот метод использует матрицу Якобиана J производных первого порядка функции F для нахождения вектора x значений параметра, который минимизирует остаточные суммы квадратов (сумму квадратных отклонений предсказанных значений от наблюдаемых).

В методе наименьших квадратов подлежащая минимизации функция f(x) представляет собой сумму квадратов.

Под F(x) имеется ввиду следующий вектор-столбец:

Подобного типа задачи широко распространены и имеют ряд практических применений, особенно при подборе модельной функции для некого набора данных, т.е. подбор нелинейных параметров. Пусть J(x) - матрица Якоби для функции F(x), то есть

,

где x из R^m.

Выбирая некоторое начальное значение x₀ последовательные приближения x_j+1 находят следующим образом:

.

Статистической оценкой или статистикой характеристики (параметра) совокупности называют приближенное значение искомой характеристики (параметра), полученное по данным выборки.

В статистике используются два вида оценок - точечные и интервальные.

Точечной статистической оценкой параметра совокупности называется конкретное числовое значение искомой характеристики.

Интервальная оценка представляет собой числовые интервалы, предположительно содержащие значение параметра совокупности.

Качество статистических оценок определяется следующими их свойствами:

- Состоятельность

Оценка считается состоятельной, если при неограниченном увеличении объема выборки[n∞(N)], ее ошибка стремится к 0.

- Несмещенность

Оценка считается несмещенной, если при данном объеме выборки n математическое ожидание ошибки равно 0.Для несмещенной оценки ее математическое ожидание точно равно математическому ожиданию характеристики выборки.

Несмещенная оценка не всегда дает хорошее приближение оцениваемого параметра, так как возможные значения получаемой оценки могут быть сильно рассеяны вокруг своего среднего значения. Поэтому оценка должна соответствовать еще одному требованию– эффективности.

- Эффективность

Оценка считается эффективной, если ее ошибка, называемая ошибкой выборки, является величиной минимальной.

11. Технология обработки экспериментальных данных методом наименьших квадратов (мнк). Линейный мнк.

Метод наименьших квадратов

Если некоторая физическая величина зависит от другой величины , то эту зависимость можно исследовать, измеряя y при различных значениях x . В результате измерений получается ряд значений:

x₁, x₂, ..., x_i, , ... , x_n;

y₁, y₂, ..., y_i, , ... , y_n.

По данным такого эксперимента можно построить график зависимости y = ƒ(x). Полученная кривая дает возможность судить о виде функции ƒ(x). Однако постоянные коэффициенты, которые входят в эту функцию, остаются неизвестными. Определить их позволяет метод наименьших квадратов. Экспериментальные точки, как правило, не ложатся точно на кривую. Метод наименьших квадратов требует, чтобы сумма квадратов отклонений экспериментальных точек от кривой, т.е. [y_i – ƒ(x_i)]² была наименьшей.

На практике этот метод наиболее часто (и наиболее просто) используется в случае линейной зависимости, т.е. когда

y = kx    или  y = a + bx.

Линейная зависимость очень широко распространена в физике. И даже когда зависимость нелинейная, обычно стараются строить график так, чтобы получить прямую линию. Например, если предполагают, что показатель преломления стекла n связан с длиной λ световой волны соотношением n = a + b/λ², то на графике строят зависимость n от λ^-2.

Рассмотрим зависимость y = kx (прямая, проходящая через начало координат). Составим величину φ – сумму квадратов отклонений наших точек от прямой

.

Величина φ всегда положительна и оказывается тем меньше, чем ближе к прямой лежат наши точки. Метод наименьших квадратов утверждает, что для k следует выбирать такое значение, при котором φ имеет минимум

или    (19)

Вычисление показывает, что среднеквадратичная ошибка определения величины k равна при этом

,   (20) где – n число измерений.

Рассмотрим теперь несколько более трудный случай, когда точки должны удовлетворить формуле y = a + bx (прямая, не проходящая через начало координат).

Задача состоит в том, чтобы по имеющемуся набору значений x_i, y_i найти наилучшие значения a и b.

Снова составим квадратичную форму φ , равную сумме квадратов отклонений точек x_i, y_i от прямой

и найдем значения a и b , при которых φ имеет минимум

 ;

 .

.

Совместное решение этих уравнений дает

  (21)

.  (22)

Среднеквадратичные ошибки определения a и b равны

  (23)

.  (24)

При обработке результатов измерения этим методом удобно все данные сводить в таблицу, в которой предварительно подсчитываются все суммы, входящие в формулы (19)–(24). Формы этих таблиц приведены в рассматриваемых ниже примерах.

МНК в случае линейной модели

Пусть регрессионная зависимость является линейной:

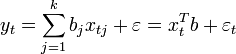
Пусть y — вектор-столбец наблюдений объясняемой переменной, а   — это  -матрица наблюдений факторов (строки матрицы — векторы значений факторов в данном наблюдении, по столбцам — вектор значений данного фактора во всех наблюдениях). Матричное представление линейной модели имеет вид:

Тогда вектор оценок объясняемой переменной и вектор остатков регрессии будут равны

соответственно сумма квадратов остатков регрессии будет равна

Дифференцируя эту функцию по вектору параметров и приравняв производные к нулю, получим систему уравнений (в матричной форме):

.

В расшифрованной матричной форме эта система уравнений выглядит следующим образом:

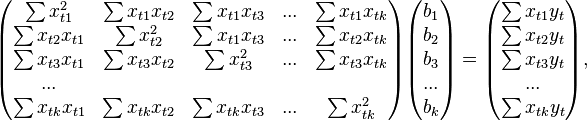 где все суммы берутся по всем допустимым значениям  .

Если в модель включена константа (как обычно), то   при всех  , поэтому в левом верхнем углу матрицы системы уравнений находится количество наблюдений  , а в остальных элементах первой строки и первого столбца — просто суммы значений переменных:   и первый элемент правой части системы —  .

Решение этой системы уравнений и дает общую формулу МНК-оценок для линейной модели:

Для аналитических целей оказывается полезным последнее представление этой формулы (в системе уравнений при делении на n, вместо сумм фигурируют средние арифметические). Если в регрессионной модели данные центрированы, то в этом представлении первая матрица имеет смысл выборочной ковариационной матрицы факторов, а вторая — вектор ковариаций факторов с зависимой переменной. Если кроме того данные ещё и нормированы на СКО (то есть в конечном итоге стандартизированы), то первая матрица имеет смысл выборочной корреляционной матрицы факторов, второй вектор — вектора выборочных корреляций факторов с зависимой переменной.

Немаловажное свойство МНК-оценок для моделей с константой — линия построенной регрессии проходит через центр тяжести выборочных данных, то есть выполняется равенство:

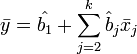
В частности, в крайнем случае, когда единственным регрессором является константа, получаем, что МНК-оценка единственного параметра (собственно константы) равна среднему значению объясняемой переменной. То есть среднее арифметическое, известное своими хорошими свойствами из законов больших чисел, также является МНК-оценкой — удовлетворяет критерию минимума суммы квадратов отклонений от неё