4. Технология численного интегрирования обыкновенных дифференциальных уравнений (оду): решение задачи Коши.
Задача Коши — одна из основных задач теории дифференциальных уравнений (обыкновенных и с частными производными); состоит в нахождении решения (интеграла) дифференциального уравнения, удовлетворяющего так называемым начальным условиям (начальным данным).
Задача Коши формулируется следующим образом: необходимо найти такое частное решение дифференциального уравнения, которое удовлетворяет определенным начальными условиям, заданным в одной точке.
Постановка задачи Коши
При решении научных и инженерных задач исследователь часто сталкивается с проблемой математического описания анализируемой динамической системы. При этом не всегда удается найти закон, устанавливающий в явном виде зависимость между величинами, хотя известно, как взаимосвязаны производные этих величин по времени и по координате в виде дифференциальных уравнений. Известно много аналитических методов решения дифференциальных уравнений, когда решение записывается в виде интеграла. Но при решении практических задач интегралы часто не выражаются в элементарных функциях. В этом случае необходимо использовать численные методы решения дифференциальных уравнений.
Рассмотрим обыкновенное дифференциальное уравнение (ОДУ) первого порядка:
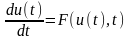(1)
с начальным условием
,
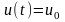(2)
где
-
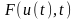некоторая заданная, в общем случае
нелинейная функция двух
переменных.
Сформулированная задача (1), (2) называется начальной задачей или задачей Коши.
Несмотря
на внешнюю простоту уравнения (1), решить
его
аналитически, т.е. найти общее
решение
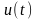с
тем, чтобы затем выделить из него
интегральную кривую
,
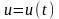проходящую через заданную точку (t0,
u0),
удается лишь для некоторых специальных
типов таких уравнений. Поэтому приходится
делать ставку на приближенные
способы
решения начальных задач для ОДУ, которые
можно разделить на 3
группы:
приближенно-аналитические методы;
графические или машинно-графические методы;
численные методы.
Наиболее
значимыми в настоящее время, характеризуемое
быстрым
развитием цифровой
вычислительной техники, являются
численные методы
решения систем
дифференциальных уравнений, предполагающие
получение
числовой таблицы приближенных
значений искомого вектора решения
на некоторой сетке
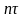(рис.1)
значений
аргумента t.
Рис.1. Равномерная сетка на отрезке
Среди численных методов решения обыкновенных дифференциальных уравнений одним из важнейших является метод конечных разностей.
Метод конечных разностей основывается:
1) на замене непрерывной области определения решения D дискретным множеством точек, называемым сеткой ωh;
2) на замене непрерывных функций дискретными (сеточными), определенными на введенной сетке изменения аргумента;
3) на замене производных, входящих в уравнение, конечными разностями. В результате вместо дифференциального уравнения получается конечно –разностное уравнение, определенное в узлах разностной сетки. Решение его сводится к отысканию значений сеточной функции в узлах сетки.
Методы численного решения задачи Коши для обыкновенных дифференциальных уравнений
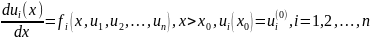
разделяются на два класса:
1) одноступенчатые методы, использующие данные о решении только в одной точке. Однако приходится вычислять функции fi(x, u) в нескольких точках (x, u). К этим методам относятся методы Рунге–Кутта и метод Решения с помощью рядов Тейлора;
2) многоступенчатые, или многошаговые, методы, не требующие много повторных вычислений функций fi(x, u), использующие данные о решении в нескольких точках, что вынуждает применять одношаговые методы для запуска метода и при изменении шага интегрирования. Это методы прогноза-коррекции, Адамса и другие.