Вариант № 20

1. Используя определение предела, доказать, что:

l

n→ ∞

im

2. Вычислить предел:

l

n→∞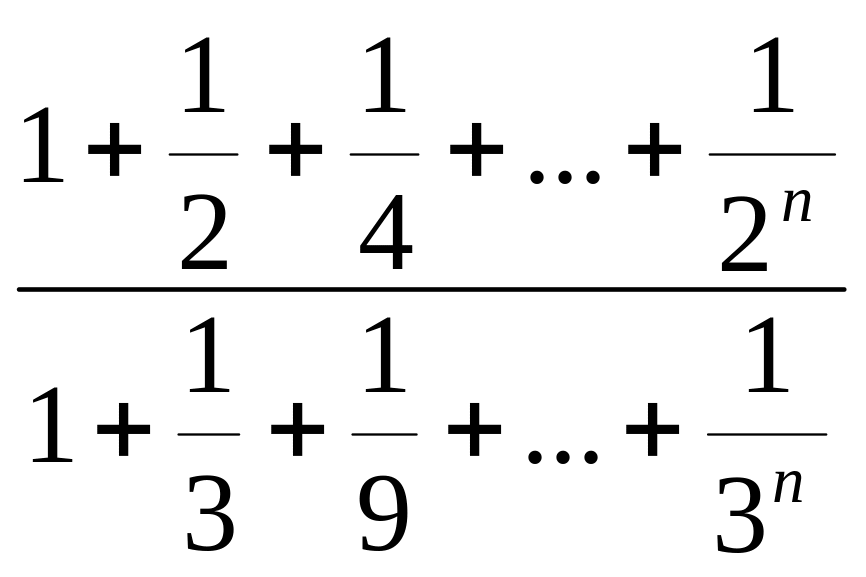

im

3. В конус вписан цилиндр. Представьте объем цилиндра как функцию радиуса его основания, зная, что радиус конуса равен 24см, а высота конуса 48см.

4. Найти область определения функции.

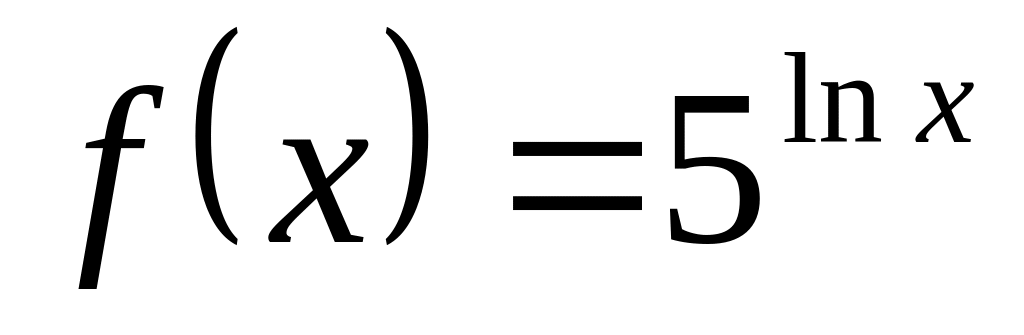
5. Найти горизонтальные асимптоты к графику функции.

6. Найти область значений функции

7. Вычислить пределы:

а

х → -1

х → 0

х →

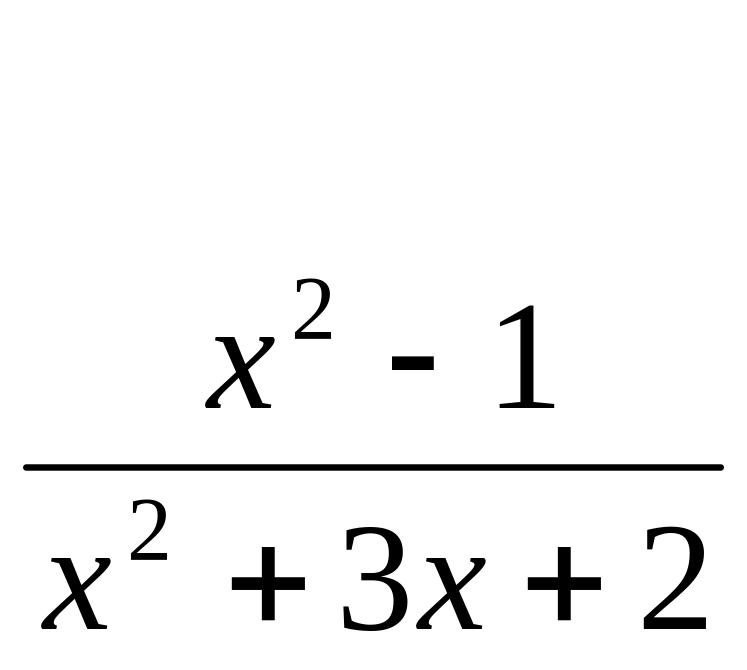) lim б) lim с) lim

8. Найти точки разрыва функции и установить их характер, если:

9. Найти значение производной функции

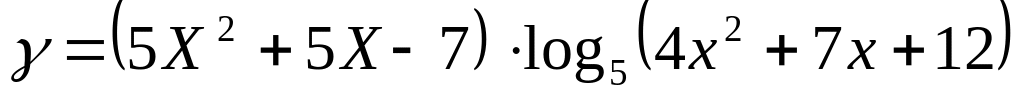
в точке

10. Найти точки перегиба, промежутки выпуклости и вогнутости графика функции

11. Найти уравнение касательной к кривой функции 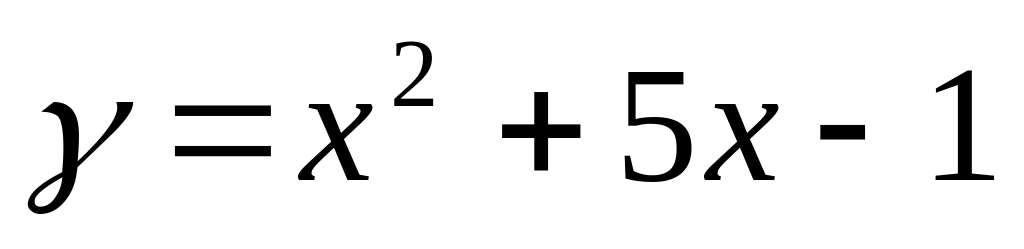в точке М(1;5)

12. Найти значение производной в точке t=0, если ,

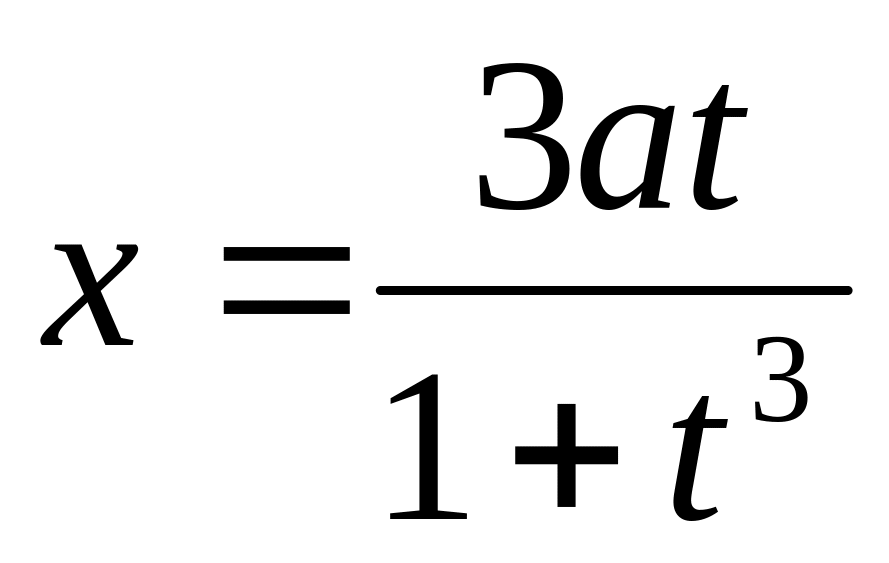13. Н

    х

    айти предел, используя правило Лопиталя ; lim

14. Найти наибольшее значение площади треугольника ОАВ, вершинами которого служат начало О системы координат, точка А , лежащая на графике функции 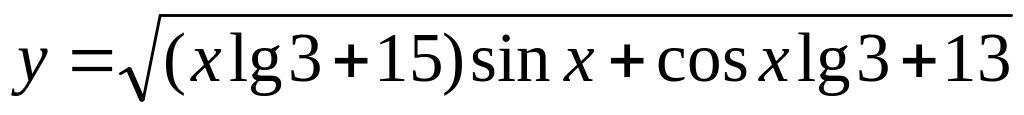, и точка В, лежащая на оси Ох и, имеющая абсциссу в два раза большую ординаты точки А.

Вариант № 21

1. Используя определение предела, доказать, что:

l

n→ ∞

im

2. Вычислить предел:

l

n→∞

im

3. В конус, высота которого равна 30см, а радиус основания 12см ,вписан цилиндр. Представьте объем этого цилиндра как функцию радиуса его основания.

4. Найти область определения функции.

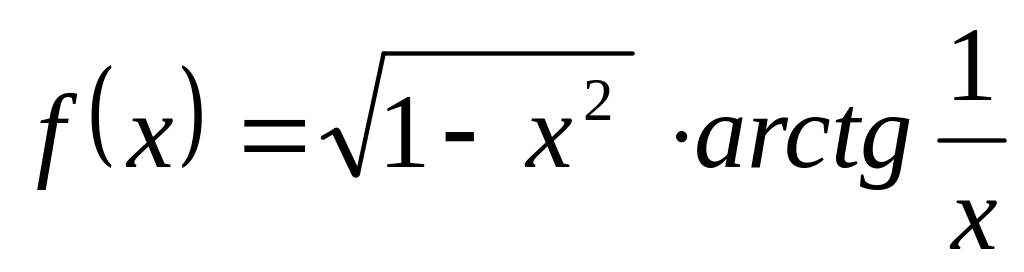
5. Найти горизонтальные асимптоты к графику функции.

6. Найти область значений функции

7. Вычислить пределы:

а

х→+∞

х → 0

х →

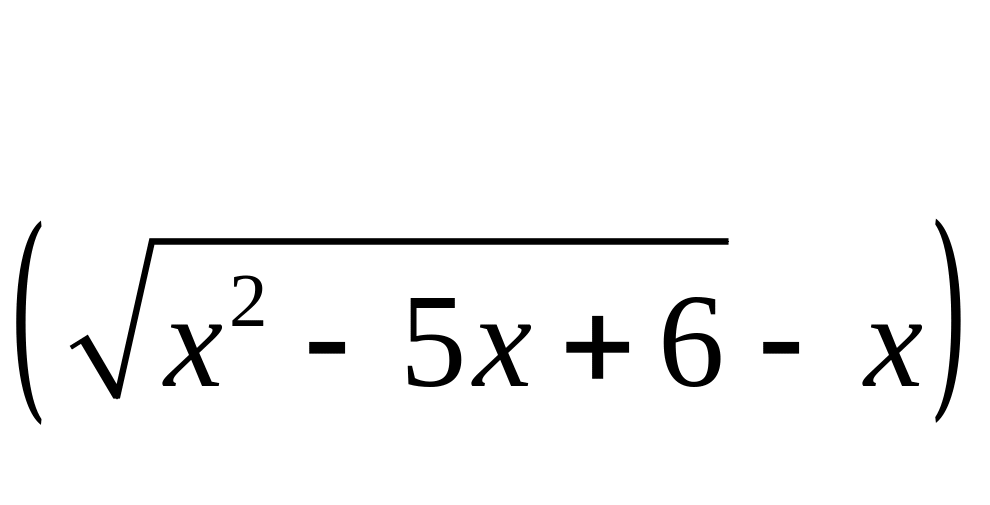) lim ; б) lim ; в) lim ;

8. Найти точки разрыва функции и установить их характер, если:

9. Найти значение производной функции 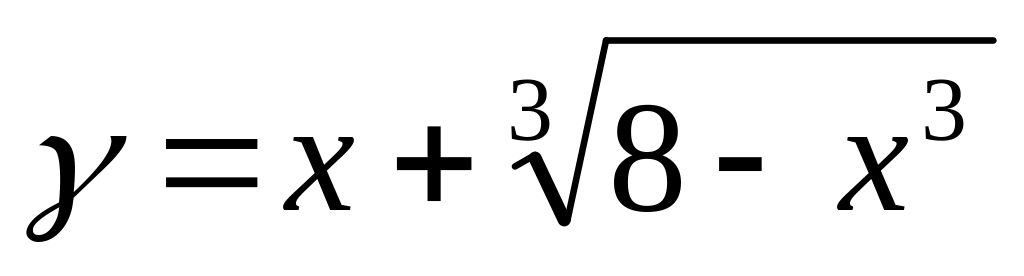в точке x=1.

10. Найти точки перегиба, промежутки выпуклости и вогнутости графика функции

11. Найти уравнение касательной к кривой 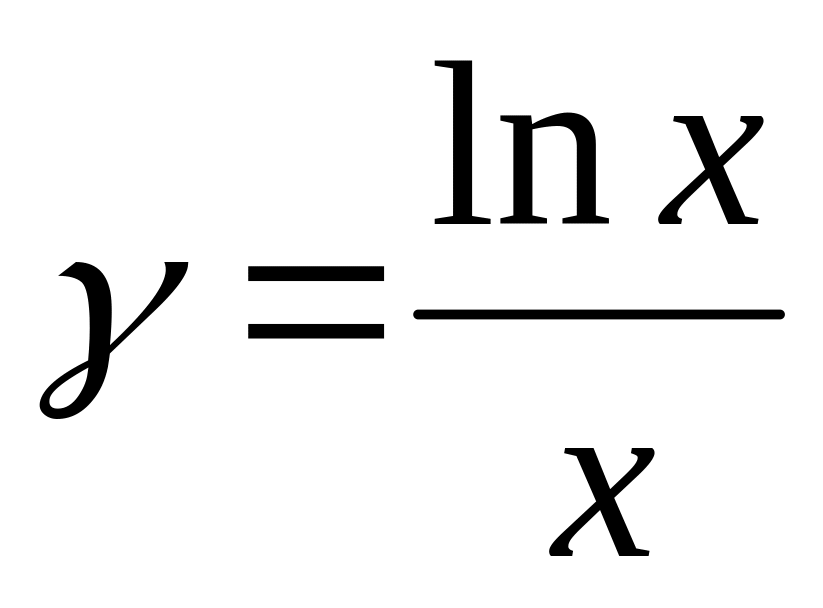в точке М(1;0)

12. Найти значение производной в точке t=0, если ,

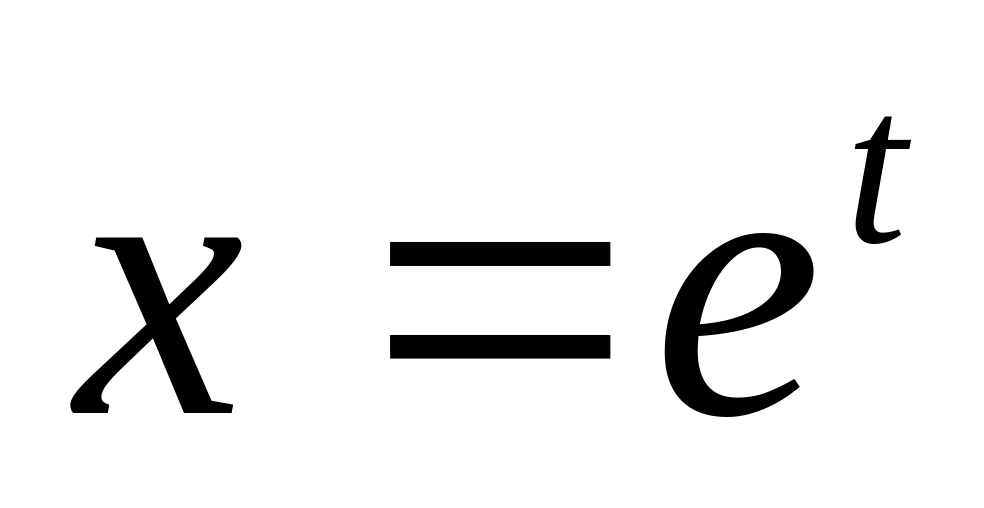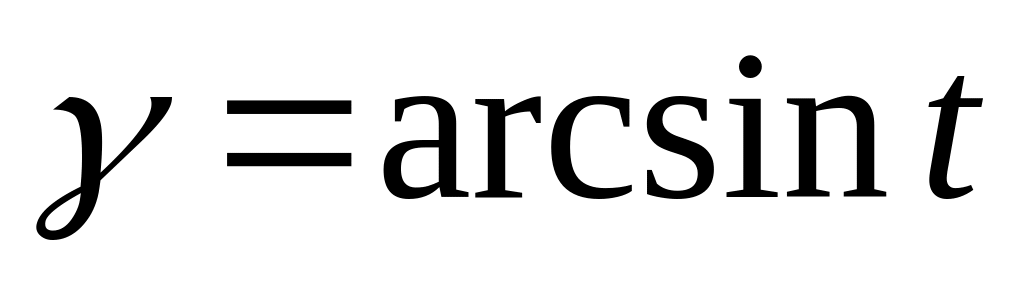
13. Н

    х →+

    айти предел, используя правило Лопиталя lim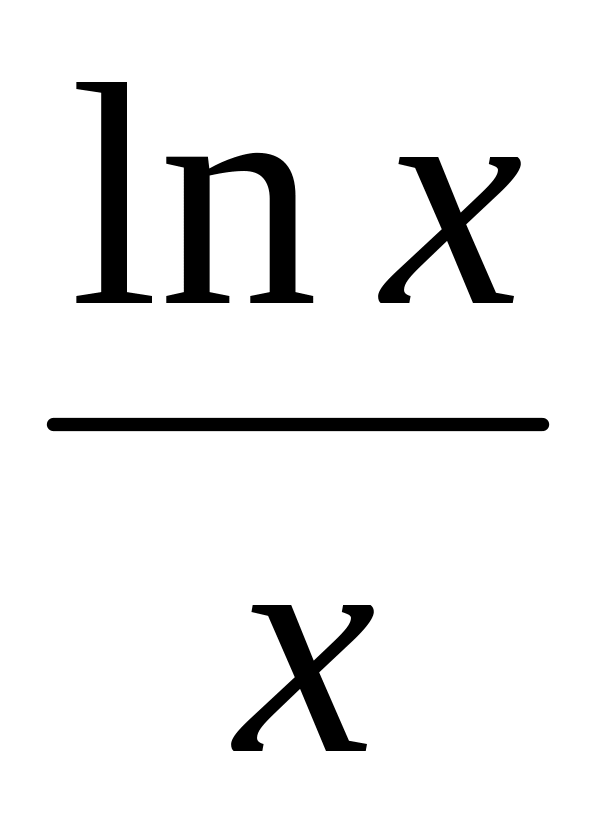

14. Найти наибольшее значение площади треугольника ОАВ, вершинами которого служат начало О системы координат, точка А , лежащая на графике функции 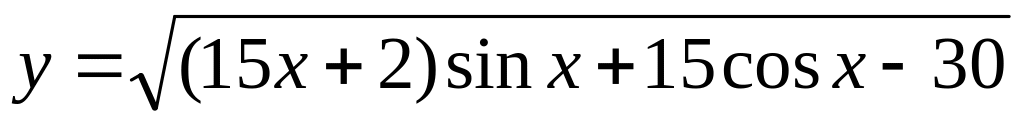, и точка В, лежащая на оси Ох и, имеющая абсциссу в два раза большую ординаты точки А.

Вариант № 22

1. Используя определение предела, доказать, что:

l

n→ ∞

im

2. Вычислить предел:

l

n→∞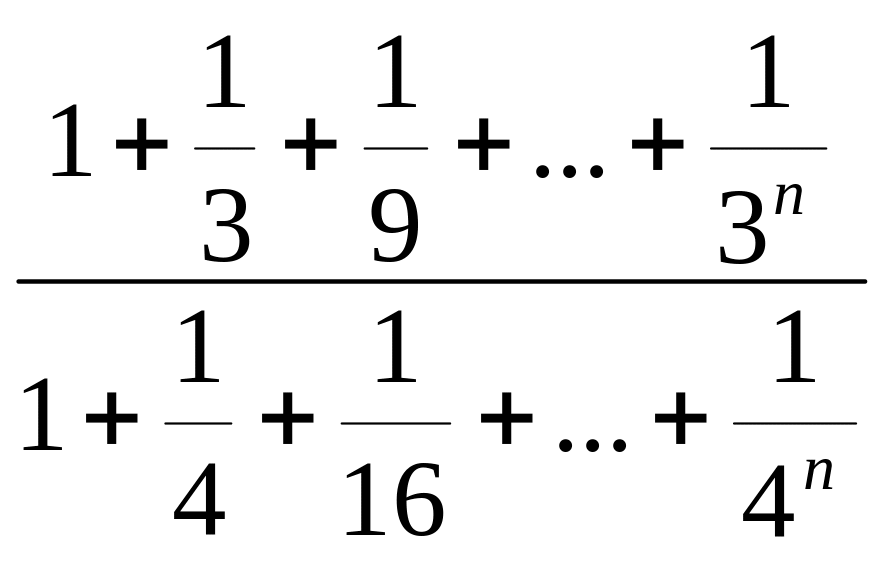

im

3. Около шара радиуса 15см описан прямой круговой конус. Представьте объем этого конуса как функцию его высоты.

4. Найти область определения функции.

5. Найти горизонтальные асимптоты к графику функции.

6. Найти область значений функции

7. Вычислить пределы:

а

х → ∞

х → 0

х →

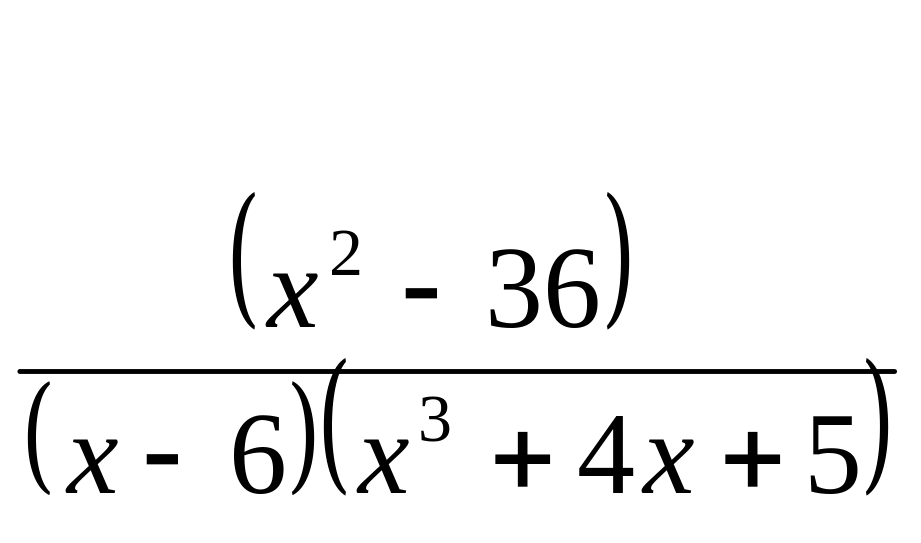) lim ; б) lim ; с) lim

8. Найти точки разрыва функции и установить их характер, если:

9. Найти значение производной функции ;

в точке

10. Найти точки перегиба, промежутки выпуклости и вогнутости графика функции

11. Найти уравнение нормали к кривой 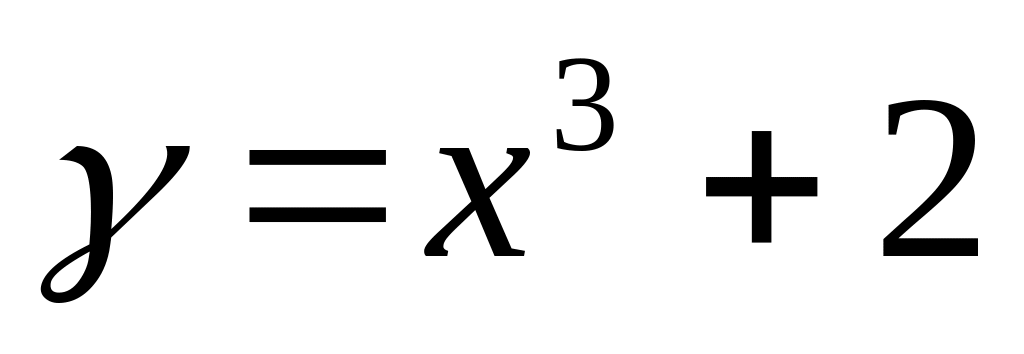в точке М(1;3)

12. Найти значение производной в точке t=0, если

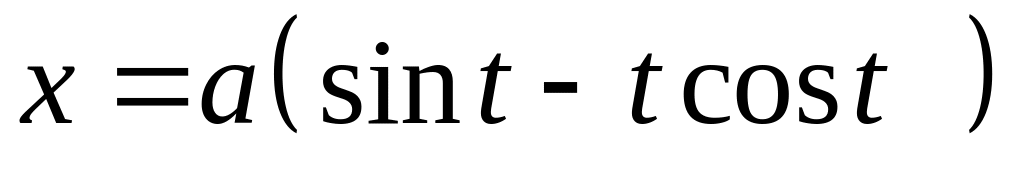
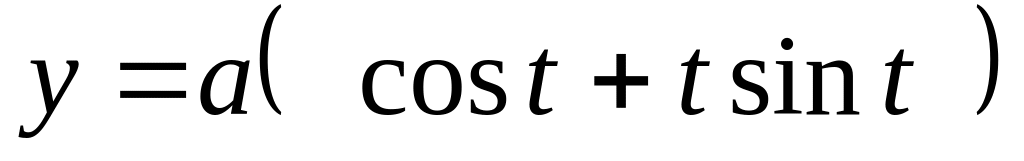
13. Н

    х → 1

    айти предел, используя правило Лопиталя lim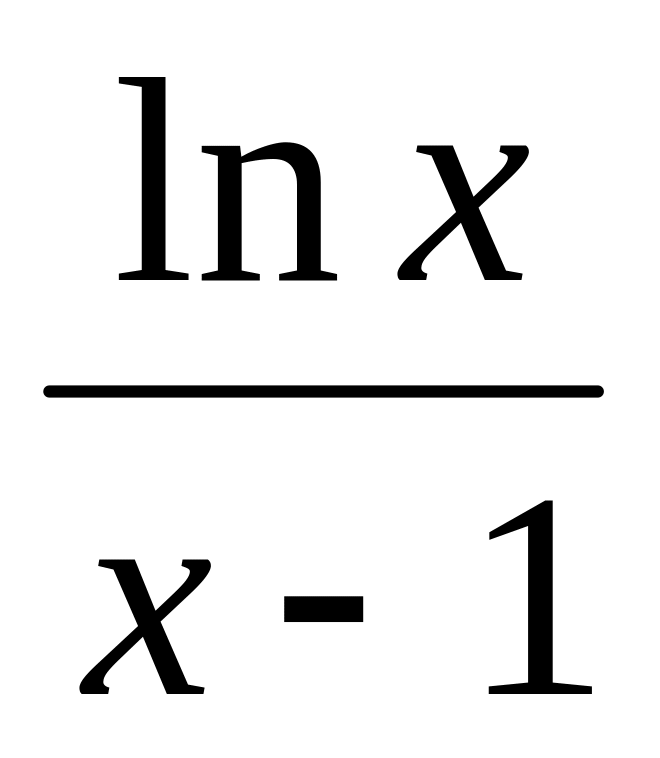

14. Найти наибольшее значение площади треугольника ОАВ, вершинами которого служат начало О системы координат, точка А , лежащая на графике функции , и точка В, лежащая на оси Ох и, имеющая абсциссу в два раза большую ординаты точки А.