Контрольная работа №4 Дифференциальное исчисление функций одной переменной Вариант № 1

1. Используя определение предела, доказать, что:

l

n→ ∞

im

2. Вычислить предел

   n→∞

   lim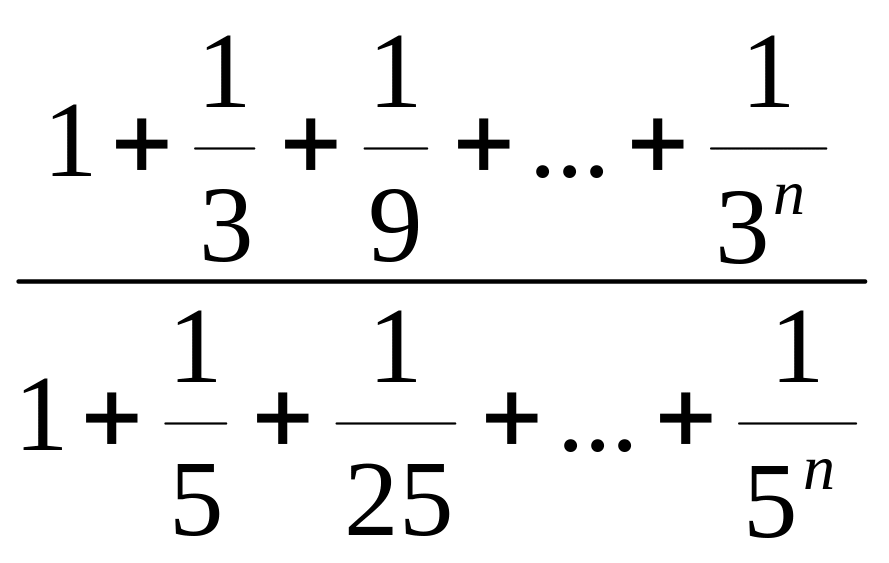

3. В шар радиуса R вписан цилиндр. Представьте объем цилиндра как функцию его высоты.

4. Найти область определения функции.

5. Найти горизонтальные асимптоты к графику функции.

6. Найти область значений функции

7. Вычислить пределы:

а

х → ∞

х → 0

х → 5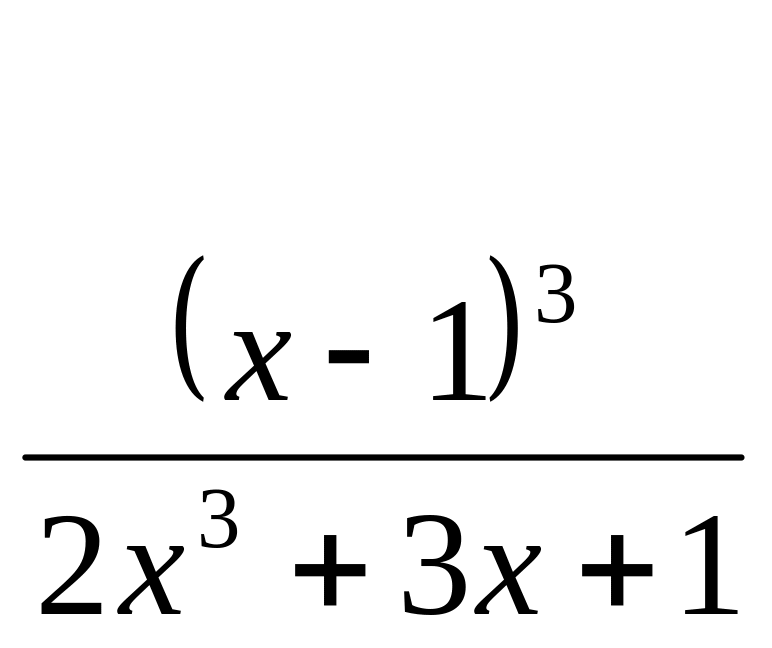

) lim б) lim с) lim

8. Найти точки разрыва функции и установить их характер, если:

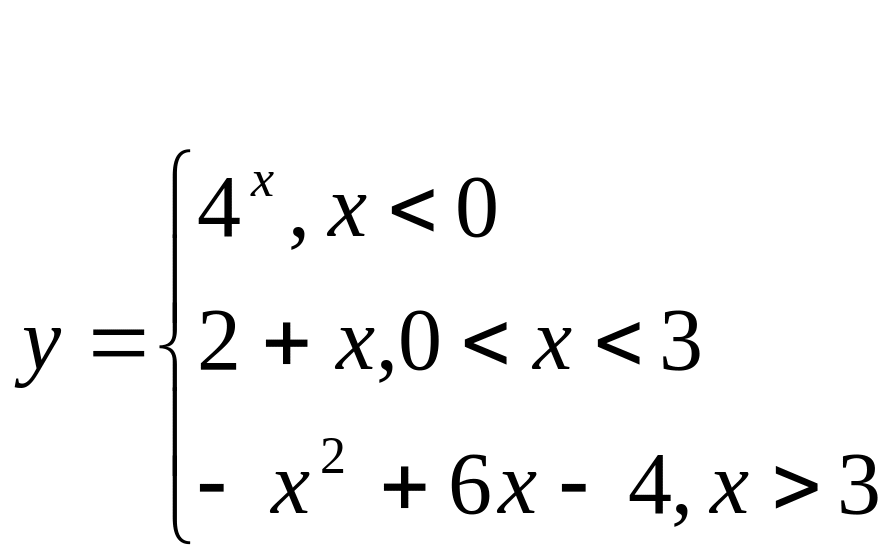
9. Найти значение производной функции

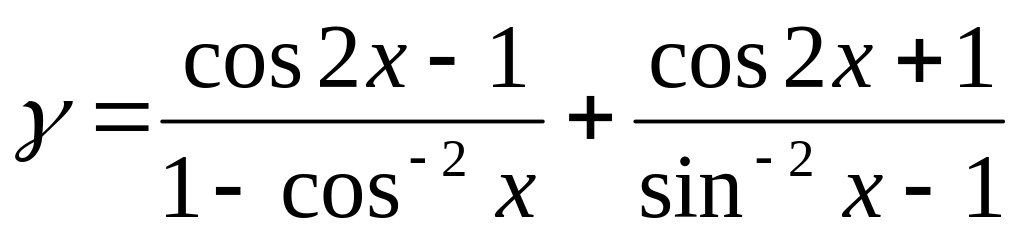
в точке

10. Найти точки перегиба, промежутки выпуклости и вогнутости графика функции

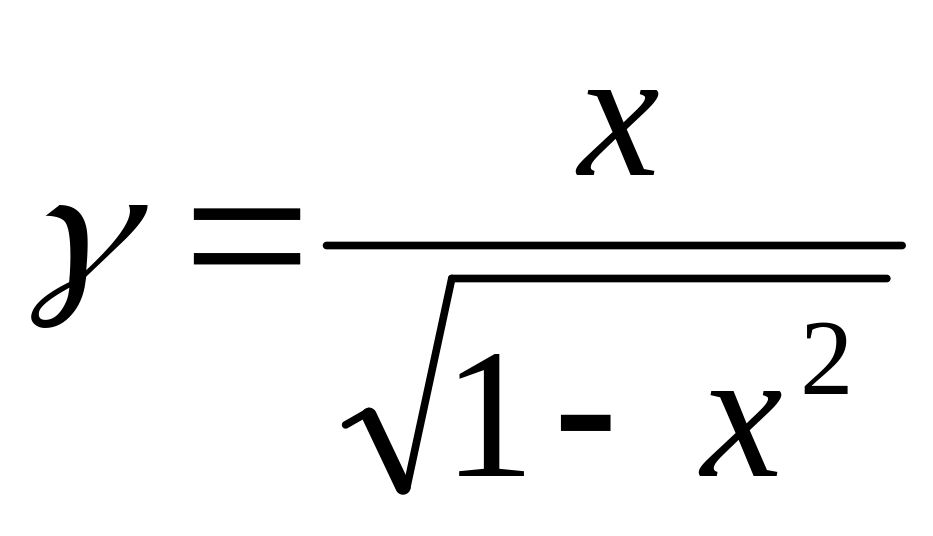
11. Составить уравнение касательной к графику функции 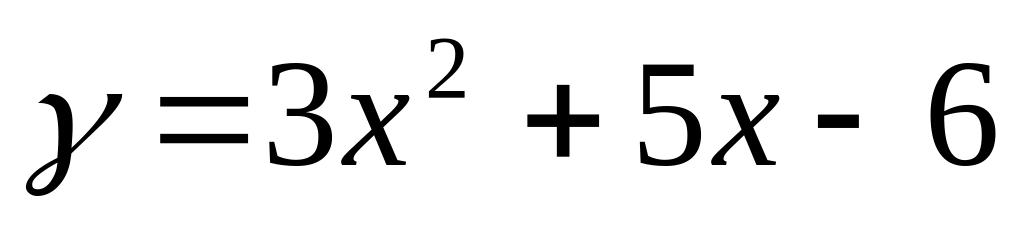параллельной прямой

12. Найти значение производной 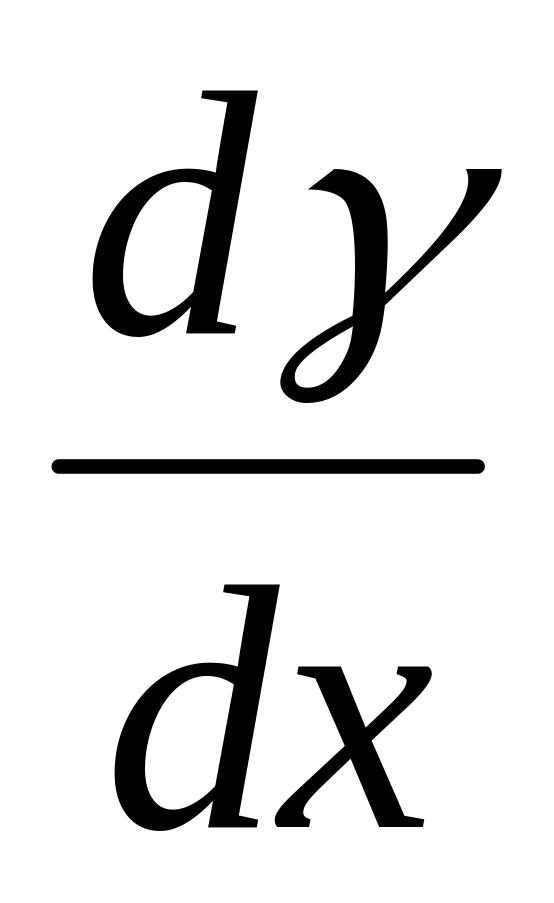в точке t=0, если ,

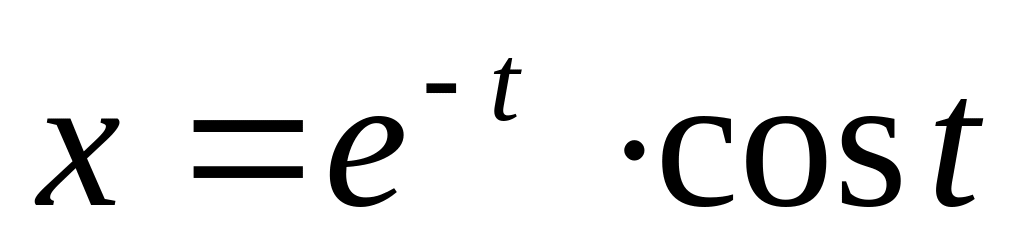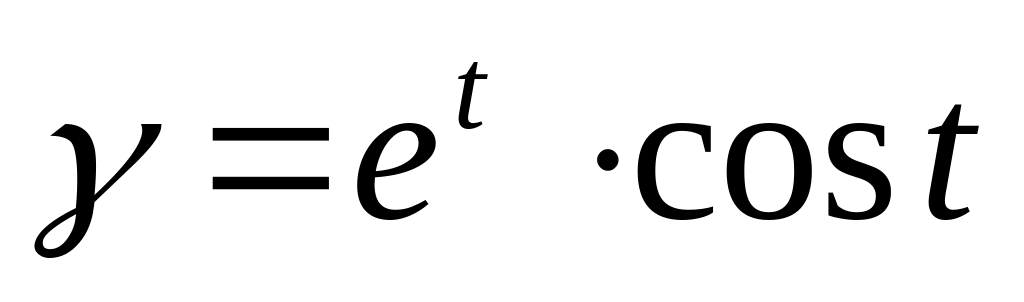
13. Н

    х → 0

    айти предел, используя правило Лопиталя lim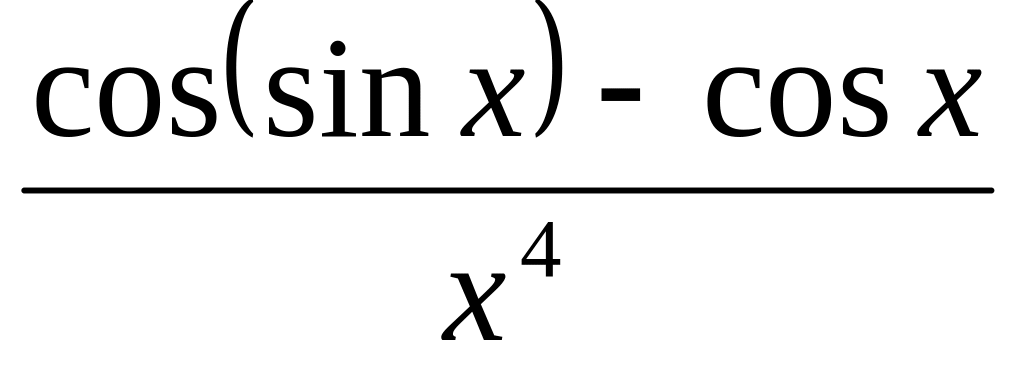

15) Найти наибольшее значение площади треугольника ОАВ, вершинами которого служат начало О системы координат, точка А , лежащая на графике функции , и точка В, лежащая на оси Ох и, имеющая абсциссу в два раза большую ординаты точки А.

Вариант№2

1)Используя определение предела доказать, что:

2)Вычислить предел:

3) В эллипс вписан прямоугольник со сторонами параллельными осям эллипса. Представить площадь этого прямоугольника в виде функции от его ширины.

4)Найти область определения функции

5) Найти горизонтальные асимптоты к графику функций

6)Найти область значений функции

7)Вычислить пределы:

а)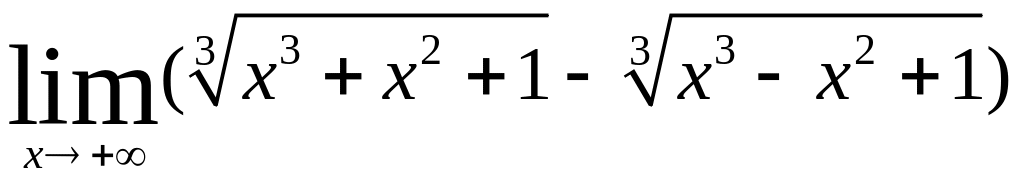

б)

в)

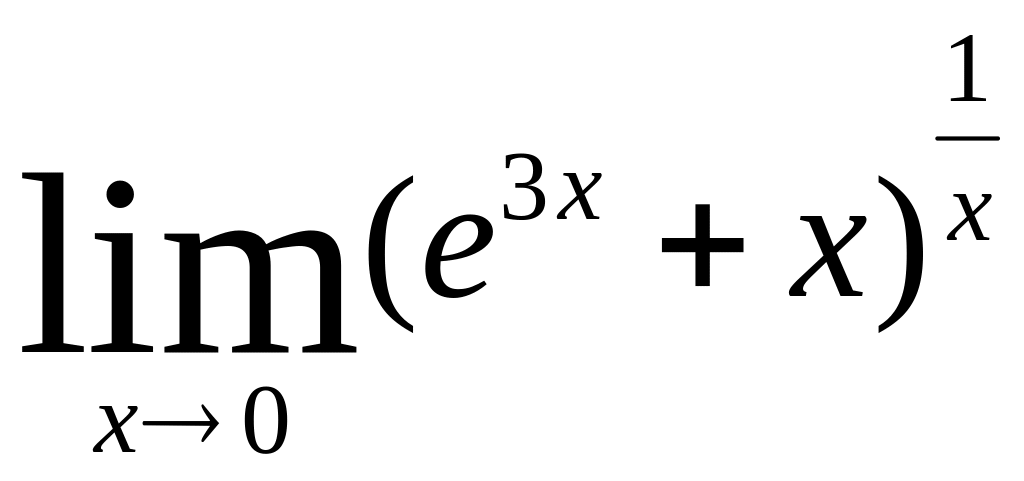
8) Найти точки разрыва функции и установить их характер, если:

9) Найти значение производной функции

в точке х=5.

10) Найти точки перегиба, промежутки выпуклости и вогнутости графика функции

11) К кривой провели касательную, параллельную вектору . Найти площадь прямоугольного треугольника, образованного при пересечении касательной с координатными осями.

12) Найти значение производной в точке t=0, если ,

13) Найти предел 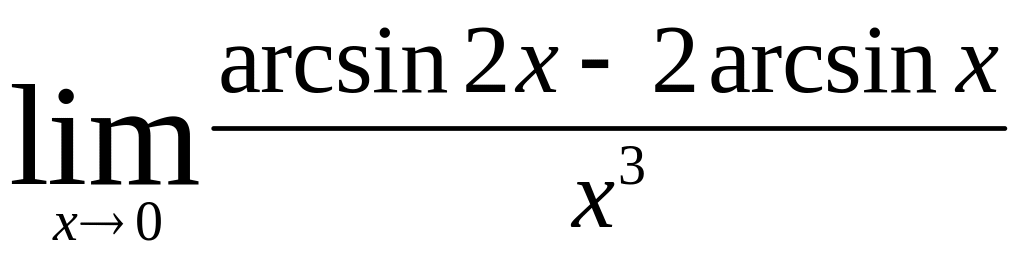, используя правило Лопиталя

14) Найти наибольшее значение площади треугольника ОАВ, вершинами которого служат начало О системы координат, точка А , лежащая на графике функции , и точка В, лежащая на оси Ох и, имеющая абсциссу в два раза большую ординаты точки А.

Вариант №3.

1)Используя определение предела доказать, что:

2)Вычислить предел:

3)Площадь поверхности консервной банки равна . Представьте объём этой банки как функцию её высоты.

4)Найти область определения функции:

5)Найти горизонтальные асимптоты к графику функций

6) Найти область значений функции

7)Вычислить пределы:

а)

б)

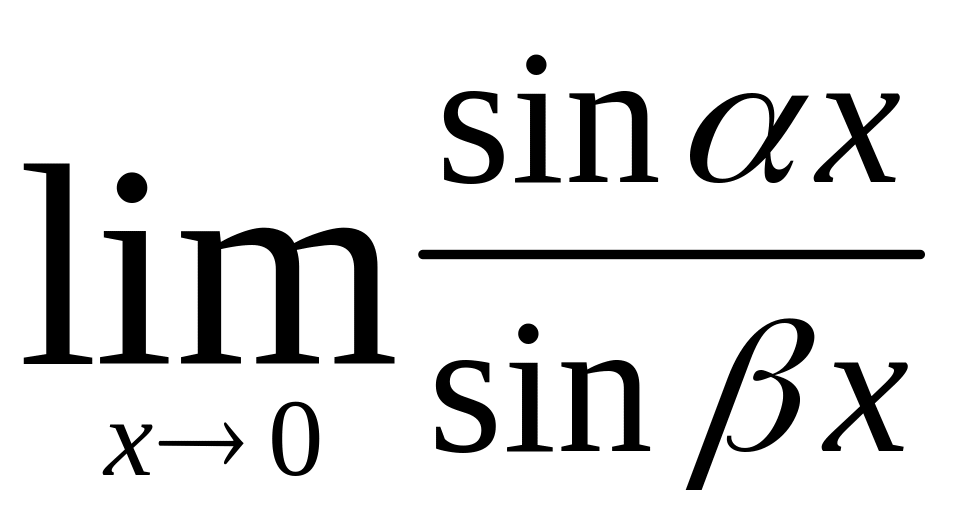
в)

8) Найти точки разрыва функции и установить их характер, если:

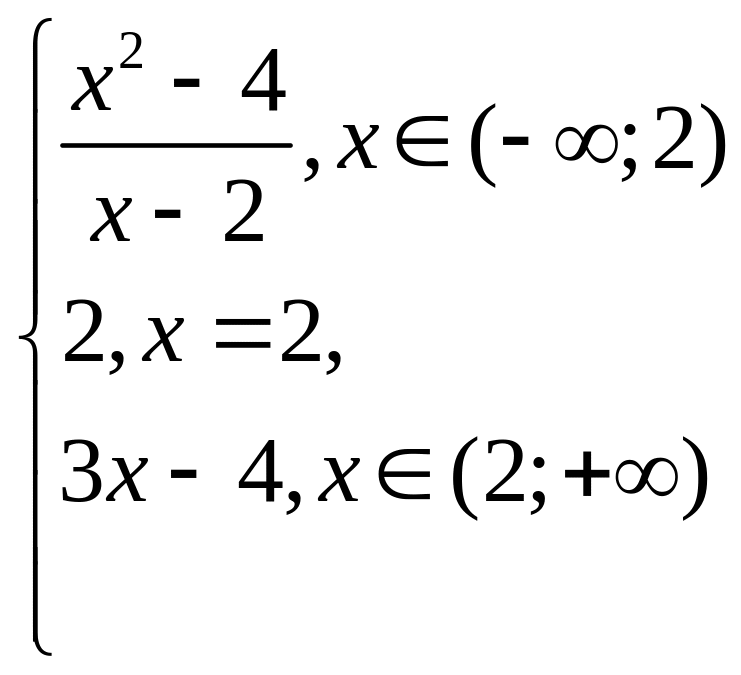
9) Найти значение производной функции

в точке x=a.

10) Найти точки перегиба, промежутки выпуклости и вогнутости графика функции

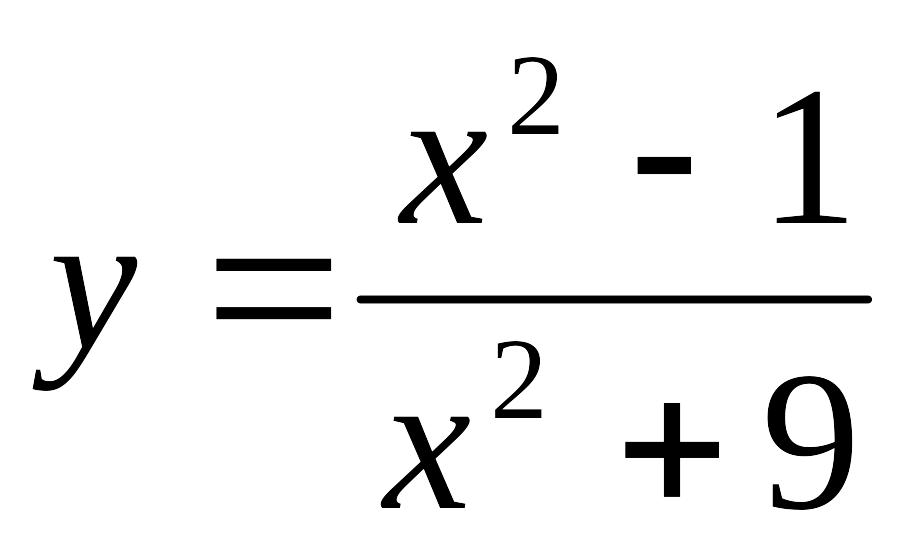
11) К кривой провели касательную, параллельную прямой 5х-2у+4. Найти площадь прямоугольного треугольника, образованного при пересечении касательной с координатными осями.

12). Найти значение производной в точке t=0, если: ,

13) Найти предел, используя правило Лопиталя

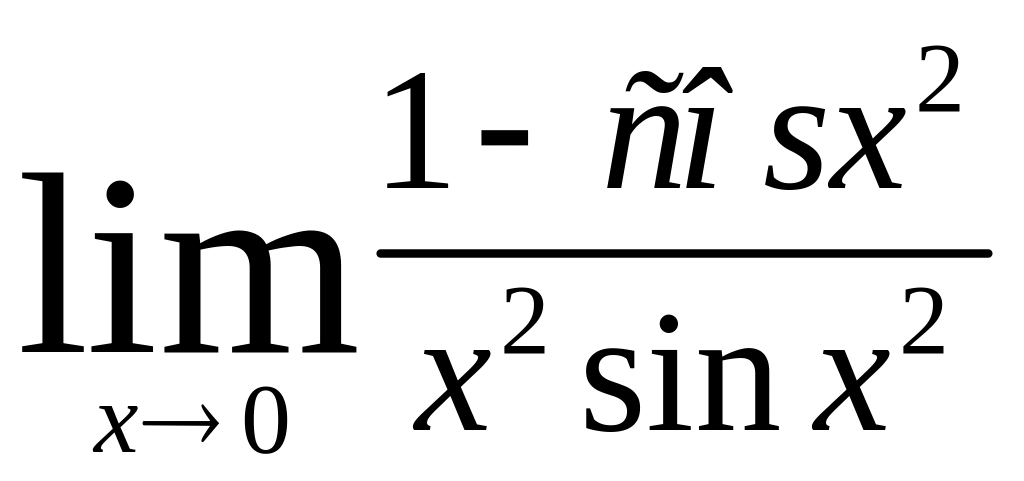
14) Найти наибольшее значение площади треугольника ОАВ, вершинами которого служат начало О системы координат, точка А , лежащая на графике функции , и точка В, лежащая на оси Ох и, имеющая абсциссу в два раза большую ординаты точки А.

Вариант №4.

1)Используя определение предела доказать, что:

2)Вычислить предел:

3)Выразите объём конической воронки с образующей, равной 20 см как функцию её высоты.

4)Найти область определения функции:

5) Найти горизонтальные асимптоты к графику функций

6)Найти область значений функции

7)Вычислить пределы:

а)

б) , где m,n натуральные числа

в)

8) Найти точки разрыва функции и установить их характер, если:

9) Найти значение производной функции в точке x=3

10) Найти точки перегиба, промежутки выпуклости и вогнутости графика функции

11) К кривой провели касательную, перпендикулярную вектору Найти площадь прямоугольного треугольника, образованного при пересечении касательной с координатными осями.

12).Найти значение производной в точке t=2,, если: ,

13) Найти предел 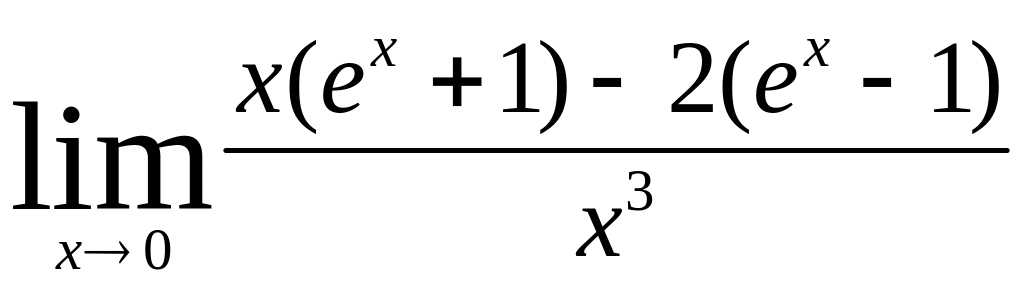, используя правило Лопиталя

14) Найти наибольшее значение площади треугольника ОАВ, вершинами которого служат начало О системы координат, точка А , лежащая на графике функции , и точка В, лежащая на оси Ох и, имеющая абсциссу в два раза большую ординаты точки А.

Вариант№5.

1)Используя определение предела доказать, что:

2) Вычислить предел:

3)В эллипс вписан прямоугольник. Представьте площадь этого прямоугольника как функцию одной из его сторон.

4)Найти область определения функции:

5) Найти горизонтальные асимптоты к графику функций

6)Найти область значений функции

7)Вычислить пределы:

a)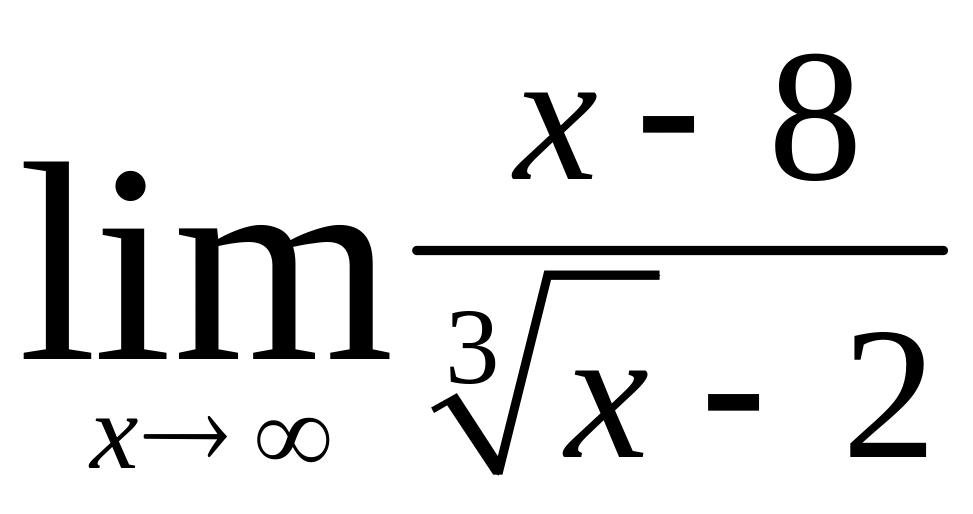

б)

с)

8) Найти точки разрыва функции и установить их характер, если:

9) Найти значение производной функции

в точке x=2.

10) Найти точки перегиба, промежутки выпуклости и вогнутости графика функции

11) К кривой провели касательную, перпендикулярную прямой 3х-у+7=0. Найти площадь прямоугольного треугольника, образованного при пересечении касательной с координатными осями.

12).Найти значение производной в точке t=0, если:

13) Найти предел , используя правило Лопиталя

14) Найти наибольшее значение площади треугольника ОАВ, вершинами которого служат начало О системы координат, точка А , лежащая на графике функции , и точка В, лежащая на оси Ох и, имеющая абсциссу в два раза большую ординаты точки А.

Вариант№6.

1)Используя определение предела доказать, что:

2)Вычислить предел:

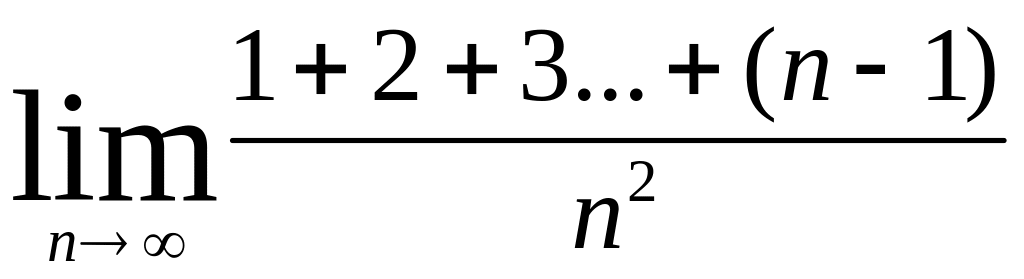
3)В полушар радиусом 10 см. вписан прямоугольный параллелепипед с квадратным основанием. Представьте объём этого параллелепипеда в виде функции его высоты.

4)Найти область определения функции:

5) Найти горизонтальные асимптоты к графику функций

6)Найти область значений функции

7)Вычислить пределы:

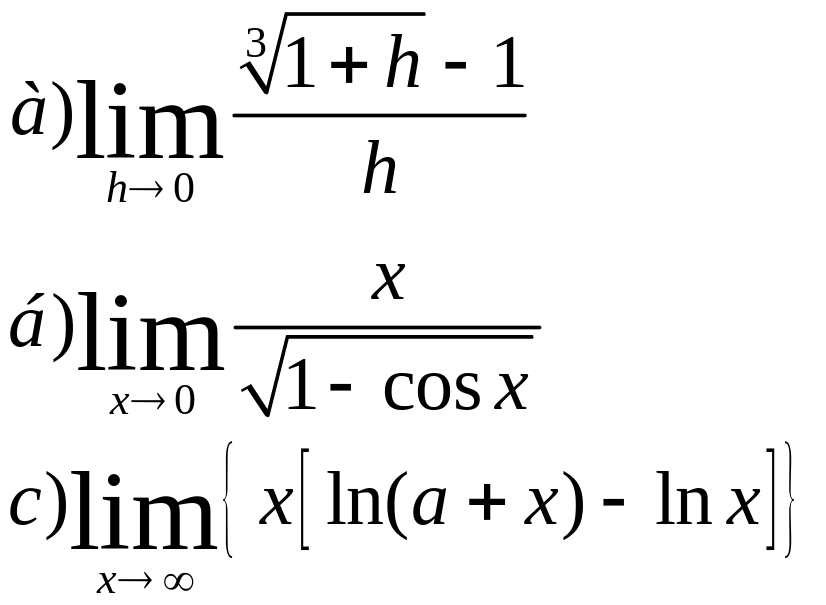
8) Найти точки разрыва функции и установить их характер, если:

9) Найти значение производной функции

в точке x=9.

10) Найти точки перегиба, промежутки выпуклости и вогнутости графика функции

11)На кривой найдите точку, в которой касательная составляет с положительным направлением оси абсцисс угол 45 градусов. Составьте уравнение этой касательной.

12).Найти значение производной в точке t=3, если:

13) Найти предел , используя правило Лопиталя

14) Найти наибольшее значение площади треугольника ОАВ, вершинами которого служат начало О системы координат, точка А , лежащая на графике функции , и точка В, лежащая на оси Ох и, имеющая абсциссу в два раза большую ординаты точки А.

Вариант№7.

1)Используя определение предела доказать, что:

2)Вычислить предел:

3)В конус вписан цилиндр. Представьте объём цилиндра как функцию радиуса его основания, зная, что радиус конуса равен 14 см., а высота конуса 58 см.

4)Найти область определения функции:

5) Найти горизонтальные асимптоты к графику функций

6)Найти область значений функции

7)Вычислить пределы:

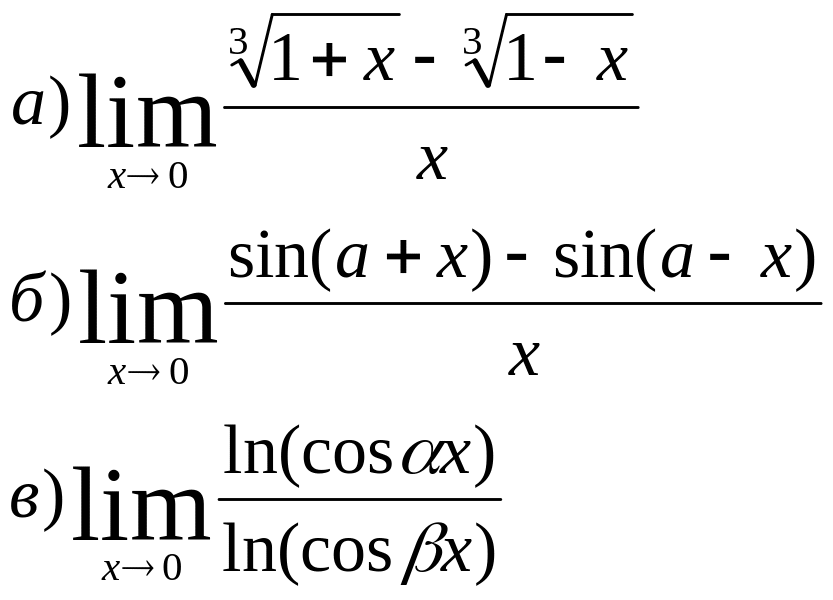
8) Найти точки разрыва функции и установить их характер, если:

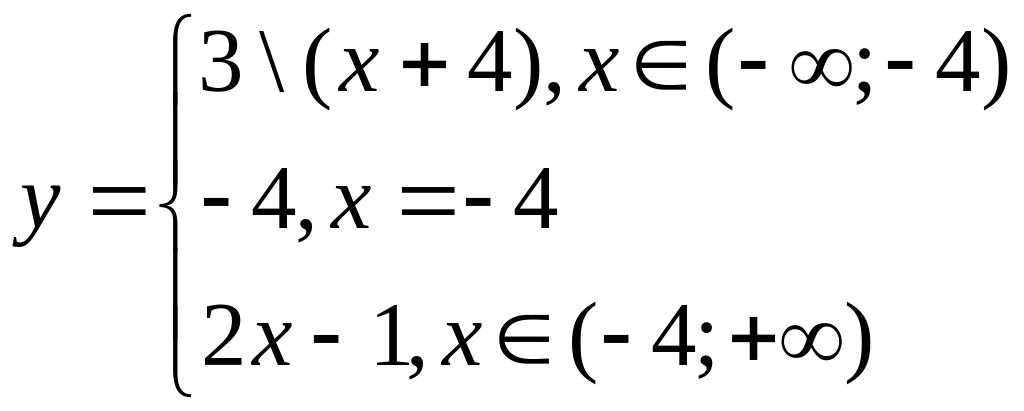
9) Найти значение производной функции

в точке x=0

10) Найти точки перегиба, промежутки выпуклости и вогнутости графика функции

11) В каких точках касательные к графикам функций

и параллельны. 12).Найти значение производной в точке t=-2, если:

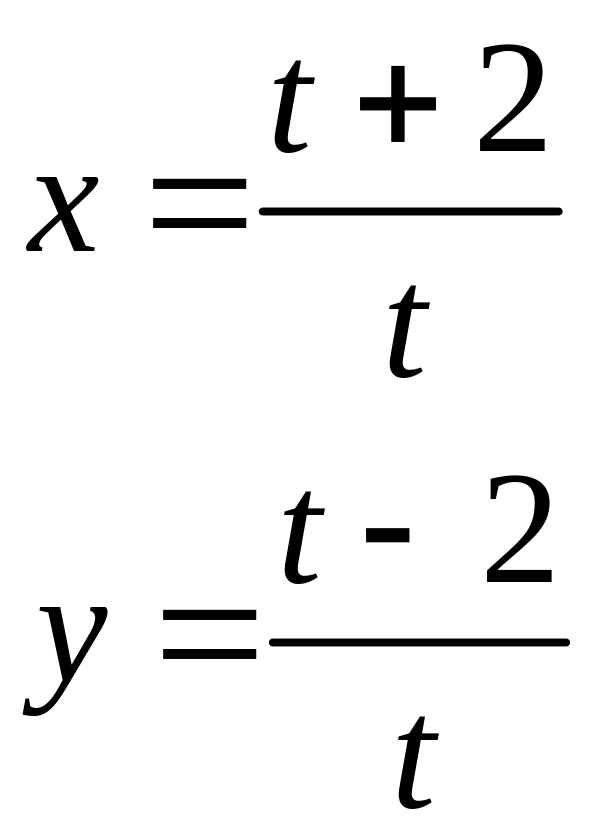
13) Найти предел , используя правило Лопиталя

14) Найти наибольшее значение площади треугольника ОАВ, вершинами которого служат начало О системы координат, точка А , лежащая на графике функции , и точка В, лежащая на оси Ох и, имеющая абсциссу в два раза большую ординаты точки А.

Вариант №8

1)Используя определение предела доказать, что:

2)Вычислить предел:

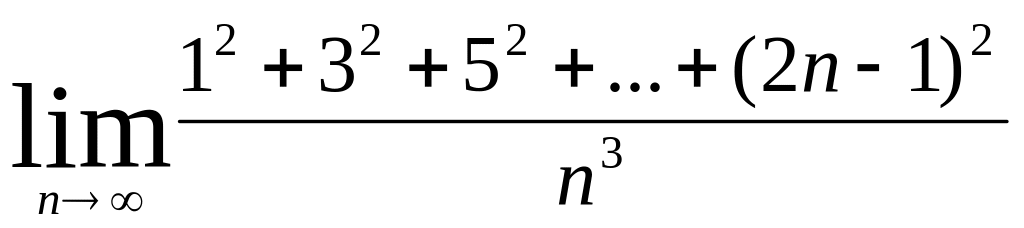
3)В конус, высота которого равна 50 см., а радиус основания 18 см. вписан цилиндр. Представьте объём этого цилиндра как функцию радиуса его основания.

4)Найти область определения функции:

5) Найти горизонтальные асимптоты к графику функций

6 )Найти область значений функции

7)Вычислить пределы:

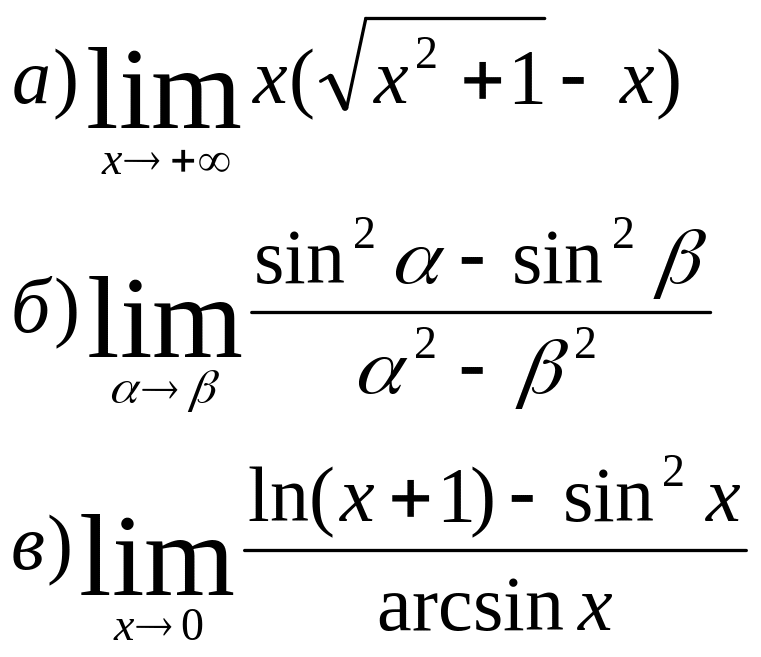
8) Найти точки разрыва функции и установить их характер, если:

9) Найти значение производной функции

в точке х=а.

10) Найти точки перегиба, промежутки выпуклости и вогнутости графика функции

11)Докажите, что касательные к линии в точках её пересечения с прямой у=1 пересекаются в начале координат.

12).Найти значение производной в точке t=1, если:

13). Найти предел , используя правило Лопиталя

14) Найти наибольшее значение площади треугольника ОАВ, вершинами которого служат начало О системы координат, точка А , лежащая на графике функции , и точка В, лежащая на оси Ох и, имеющая абсциссу в два раза большую ординаты точки А.

Вариант №9.

1)Используя определение предела доказать, что:

2)Вычислить предел:

3) Представьте площадь боковой поверхности конуса, вписанного в шар радиусом 24 см. как функцию высоты конуса.

4)Найти область определения функции:

5) Найти горизонтальные асимптоты к графику функций

6)Найти область значений функции

7)Вычислить пределы:

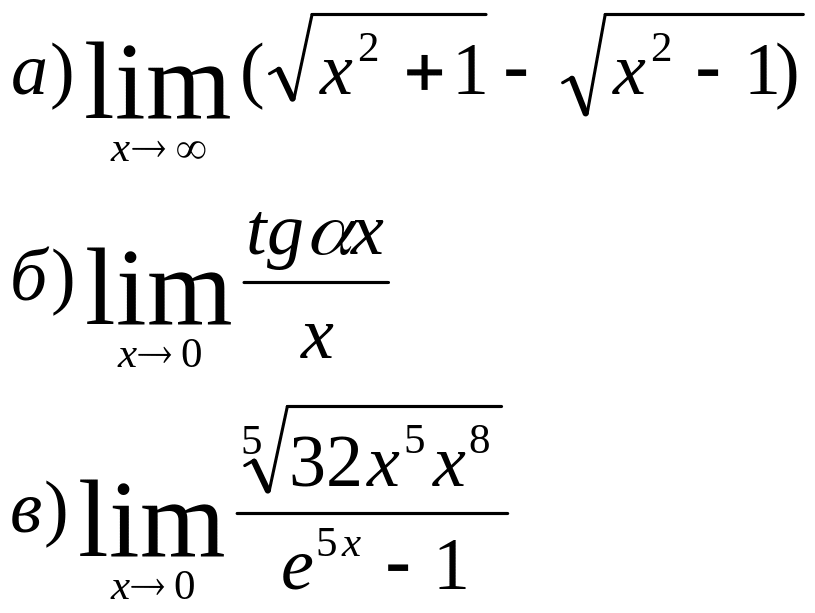
8) Найти точки разрыва функции и установить их характер, если:

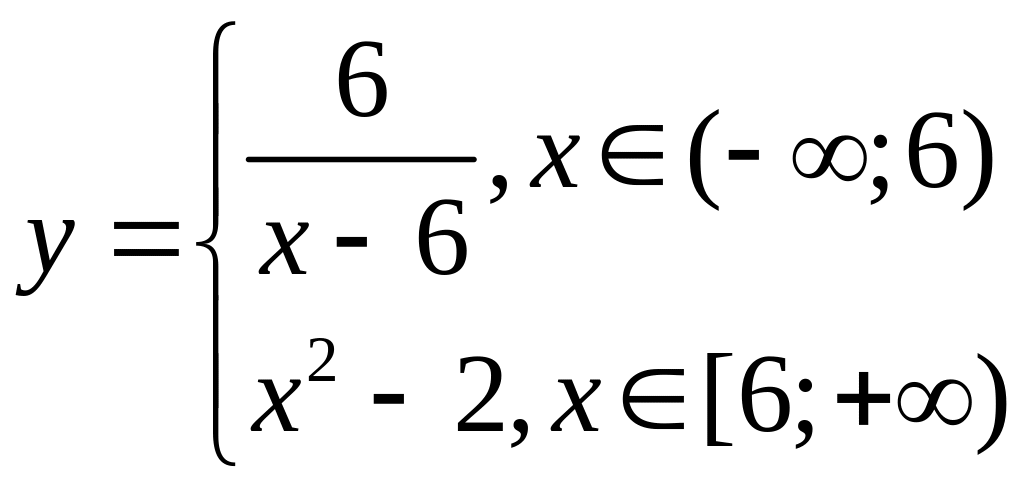
9) Найти значение производной функции в точке

10) Найти точки перегиба, промежутки выпуклости и вогнутости графика функции

11)Найдите координатные точки пересечения с осями координат тех касательных к графику функции , у которых угловой коэффициент =3.

12).Найти значение производной в точке t=0, если:

13) Найти предел , используя правило Лопиталя

14) Найти наибольшее значение площади треугольника ОАВ, вершинами которого служат начало О системы координат, точка А , лежащая на графике функции , и точка В, лежащая на оси Ох и, имеющая абсциссу в два раза большую ординаты точки А.

Вариант №10.

1)Используя определение предела доказать, что:

2)Вычислить предел

3)Около шара радиусом 30 см. описан прямой круговой конус. Представьте объём этого конуса как функцию его высоты.

4)Найти область определения функции

5) Найти горизонтальные асимптоты к графику функций

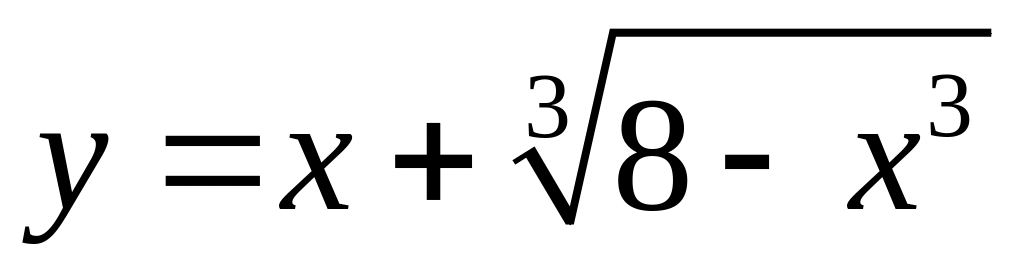
6)Найти область значений функции

7)Вычислить пределы:

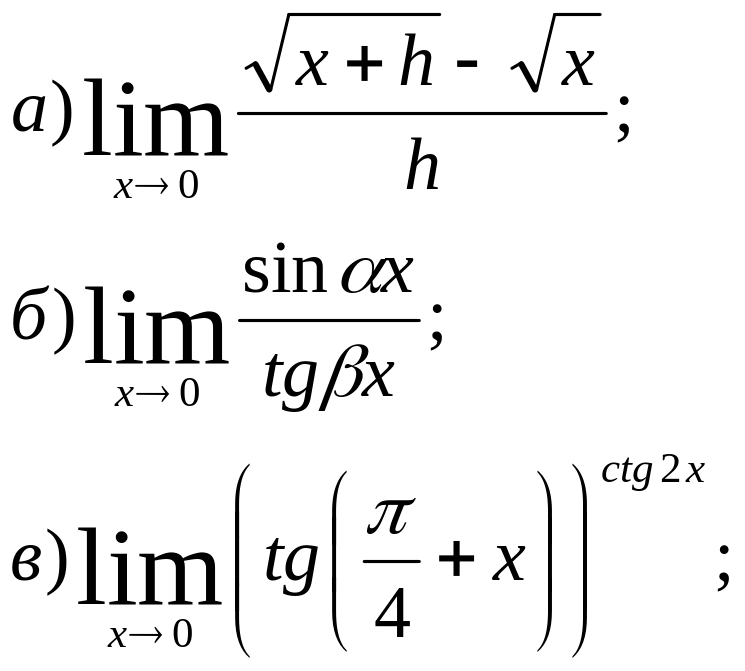
8) Найти точки разрыва функции и установить их характер, если:

9) Найти значение производной функции

в точке x=3.

10) Найти точки перегиба, промежутки выпуклости и вогнутости графика функции

11)Составить уравнение касательной к параболе в точке

12).Найти значение производной в точке t=3, если:

13) Найти предел , используя правило Лопиталя

14) Найти наибольшее значение площади треугольника ОАВ, вершинами которого служат начало О системы координат, точка А , лежащая на графике функции , и точка В, лежащая на оси Ох и, имеющая абсциссу в два раза большую ординаты точки А.

Вариант№11.

1)Используя определение предела доказать, что:

2)Вычислить предел:

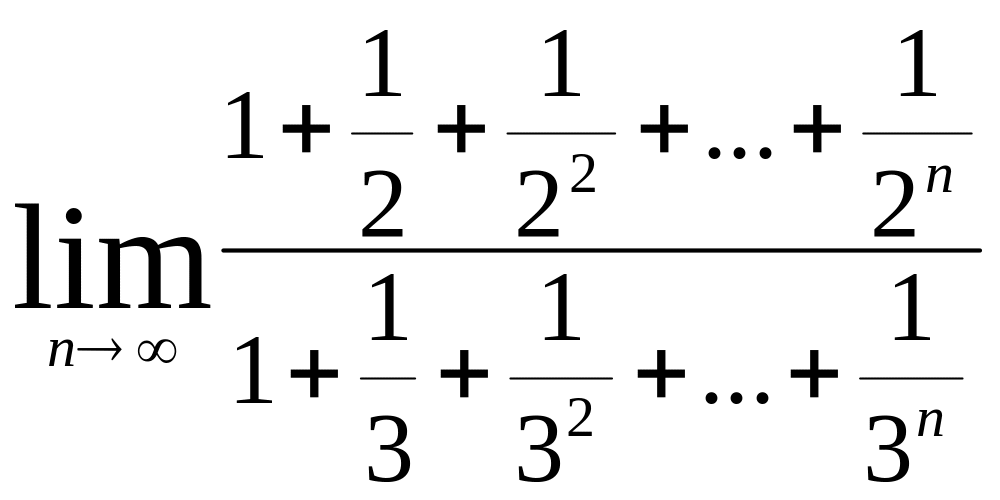
3) Цилиндр завершён снизу полушаром. Известно, что объем этого тела равен 24. Представьте площадь полной поверхности данного тела как функцию радиуса основания цилиндра.

4)Найти область определения функции

5) Найти горизонтальные асимптоты к графику функций

6)Найти область значений функции

7)Вычислить пределы:

8) Найти точки разрыва функции и установить их характер, если:

9) Найти значение производной функции в точке x=1.

10) Найти точки перегиба, промежутки выпуклости и вогнутости графика функции

11)Составить уравнение касательной к графику функции в точках пересечения с осью Ох.

12).Найти значение производной в точке t=0, если:

13) Найти предел , используя правило Лопиталя

14) Найти наибольшее значение площади треугольника ОАВ, вершинами которого служат начало О системы координат, точка А , лежащая на графике функции , и точка В, лежащая на оси Ох и, имеющая абсциссу в два раза большую ординаты точки А.

Вариант №12.

1)Используя определение предела доказать, что:

2)Вычислить предел:

3) Через точку М(3;4) проведена прямая, отсекающая в первом координатном угле прямоугольный треугольник. Представьте длину гипотенузы этого треугольника как функцию одного из его катетов.

4)Найти область определения функции:

5) Найти горизонтальные асимптоты к графику функций

6)Найти область значений функции

7)Вычислить пределы:

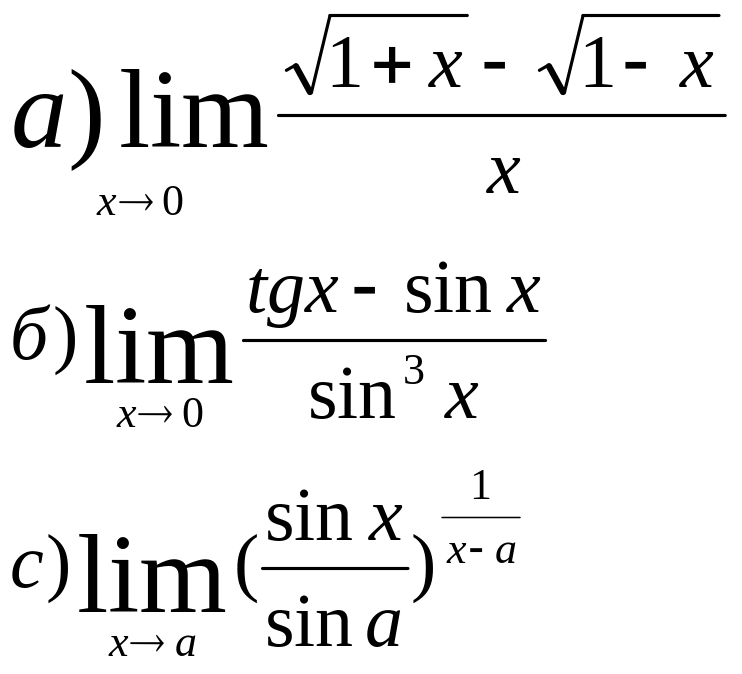
8) Найти точки разрыва функции и установить их характер, если:

9) Найти значение производной функции в точке х=а.

10) Найти точки перегиба, промежутки выпуклости и вогнутости графика функции

11) Составить уравнение касательной к графику функции у=lnx в точках пересечения с осью Ох.

12).Найти значение производной в точке t=0, если: x=t-sint, y=1-cost

13) Найти предел 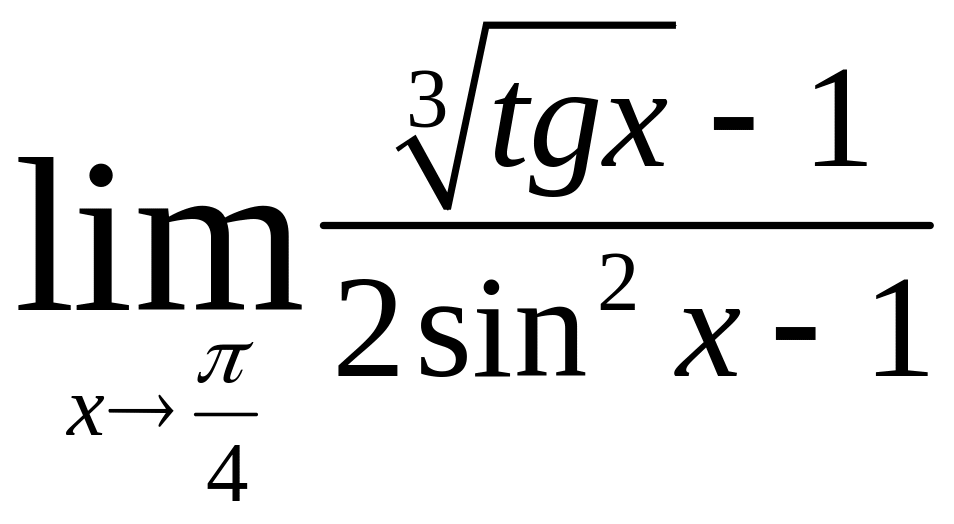, используя правило Лопиталя

14) Найти наибольшее значение площади треугольника ОАВ, вершинами которого служат начало О системы координат, точка А , лежащая на графике функции , и точка В, лежащая на оси Ох и, имеющая абсциссу в два раза большую ординаты точки А.

Вариант №13.

1)Используя определение предела доказать, что:

2)Вычислить предел:

3) Через точку М(2;5) проведена прямая, отсекающая в первом координатном угле прямоугольный треугольник. Представьте площадь этого треугольника как функцию одного из его катетов.

4). Найти область определения функции

5) Найти горизонтальные асимптоты к графику функций

6)Найти область значений функции

7)Вычислить пределы:

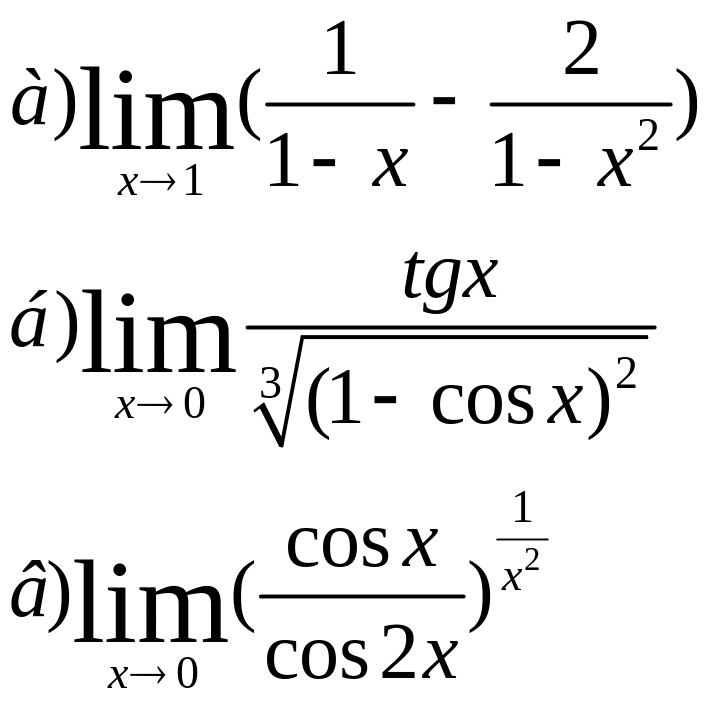
8) Найти точки разрыва функции и установить их характер, если:

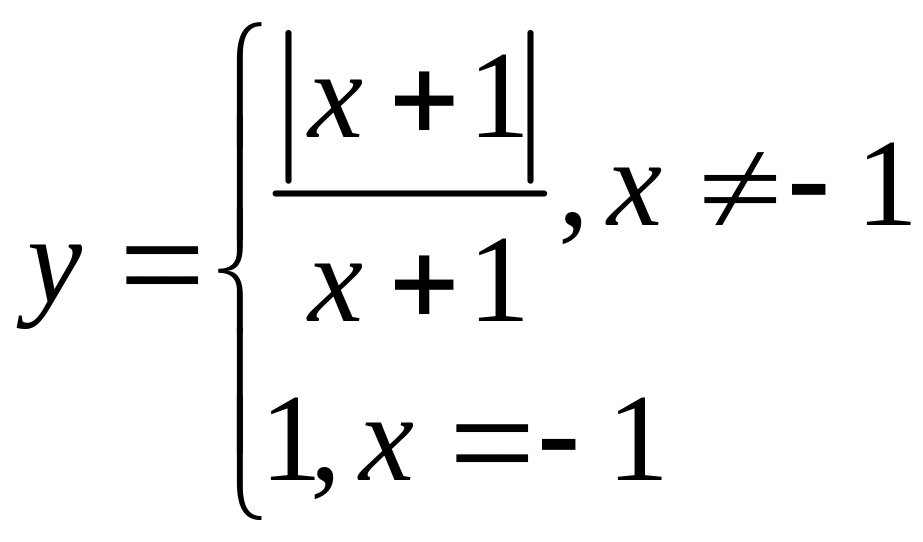
9) Найти значение производной функции в точке x=5.

10) Найти точки перегиба, промежутки выпуклости и вогнутости графика функции

11) Составить уравнение касательной к графику функции в точках пересечения с осью Оу.

12).Найти значение производной в точке t=0, если

13) Найти предел , используя правило Лопиталя

14) Найти наибольшее значение площади треугольника ОАВ, вершинами которого служат начало О системы координат, точка А , лежащая на графике функции , и точка В, лежащая на оси Ох и, имеющая абсциссу в два раза большую ординаты точки А.

Вариант №14.

1)Используя определение предела доказать, что

2)Вычислить предел:

3)В эллипсе вписан прямоугольник. Представьте площадь этого прямоугольника как функцию одной из его сторон.

4)Найти область определения функции

5) Найти горизонтальные асимптоты к графику функций

6)Найти область значений функции

7)Вычислить пределы:

8) Найти точки разрыва функции и установить их характер, если:

9) Найти значение производной функции в точке х=1.

10) Найти точки перегиба, промежутки выпуклости и вогнутости графика функции

11)При каких значениях х касательные к графику функции параллельны прямой у=х.

12).Найти значение производной в точке t=0, если

13) Найти предел 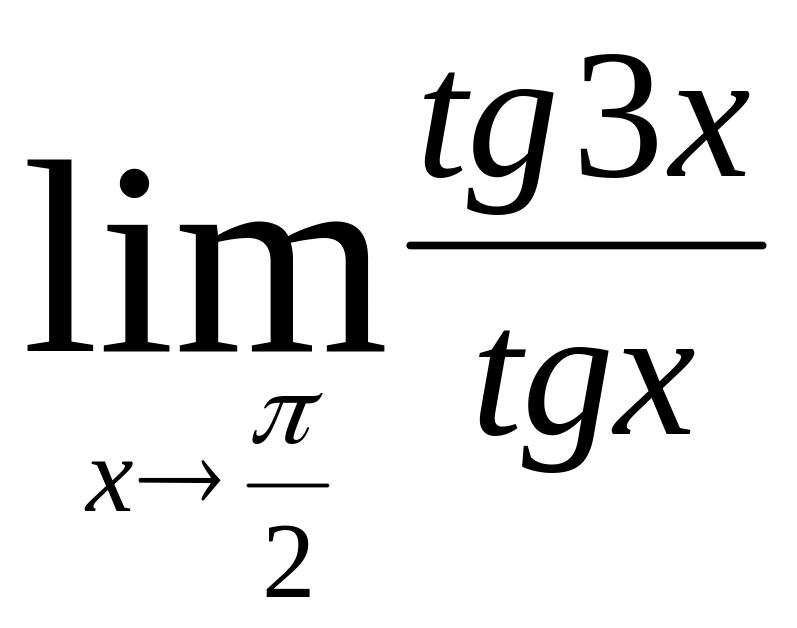, используя правило Лопиталя

14) Найти наибольшее значение площади треугольника ОАВ, вершинами которого служат начало О системы координат, точка А , лежащая на графике функции , и точка В, лежащая на оси Ох и, имеющая абсциссу в два раза большую ординаты точки А.

Вариант №15.

1)Используя определение предела доказать, что:

2)Вычислить предел:

3) Представьте площадь поверхности консервной банки, имеющей форму цилиндра вместимостью как функцию радиуса её основания.

4)Найти область определения функции:

5) Найти горизонтальные асимптоты к графику функций

6)Найти область значений функции

7)Вычислить пределы:

8) Найти точки разрыва функции и установить их характер, если:

9) Найти значение производной функции в точке х=а.

10) Найти точки перегиба, промежутки выпуклости и вогнутости графика функции

11)В точках (0;0),(2;1),(4;0) проведены касательные к параболе .Найти углы их наклона к оси Ох.

12).Найти значение производной в точке t=0, , если:

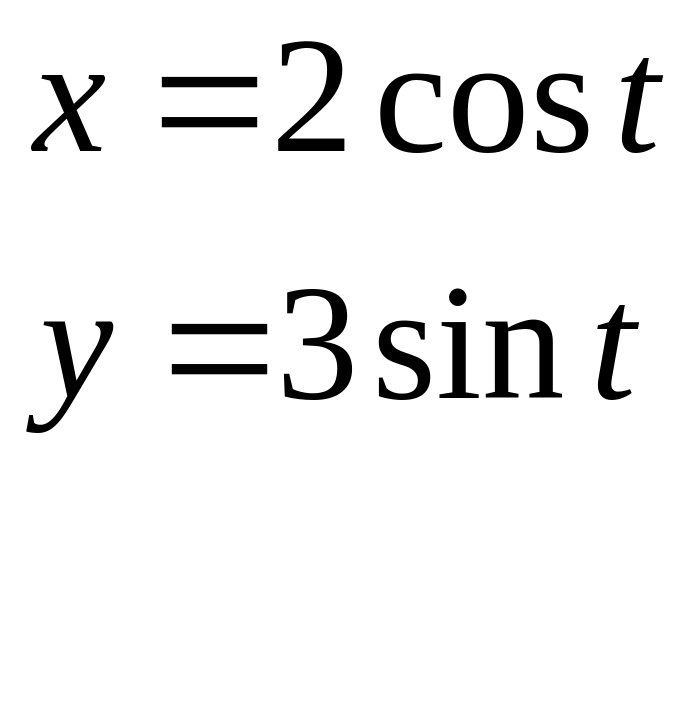
13) Найти предел , используя правило Лопиталя

14) Найти наибольшее значение площади треугольника ОАВ, вершинами которого служат начало О системы координат, точка А , лежащая на графике функции , и точка В, лежащая на оси Ох и, имеющая абсциссу в два раза большую ординаты точки А.