Министерство образования и науки Российской Федерации

Государственное образовательное учреждение высшего профессионального образования

«Национальный исследовательский томский политехнический университет» а. Ю. Чернышев, и. А. Чернышев моделирование в электроприводе

Рекомендовано в качестве учебно-методического пособия

Редакционно-издательским советом

Томского политехнического университета

Издательство

Томского политехнического университета

2012

	УДК 62-83 (075.8) ББК 31 271Я73 Ч–496
Ч–496	Чернышев А.Ю. Моделирование в электроприводе / А.Ю. Чернышев, И.А. Чернышев; Томский политехнический университет. – Томск: Изд-во Томского политехнического университета, 2012. – 157 с.

В учебно-методическом пособии рассмотрены вопросы выбора двигателя по мощности и последовательность расчета статических и динамических характеристик электроприводов постоянного и переменного тока с релейно-контакторным управлением при пуске, регулировании скорости и торможении; представлены методика и примеры расчета параметров якорной цепи двигателей постоянного тока и схемы замещения асинхронных двигателей.

Пособие подготовлено на кафедре электропривода и электрооборудования ТПУ и предназначено для студентов, обучающихся по специальности 140604 «Электропривод и автоматика промышленных установок и технологических комплексов».

УДК 62-83 (075.8)

ББК 31.291Я73

Рецензенты

Доктор технических наук, профессор кафедры конструирования

электронно-вычислительной аппаратуры ТУСУР

В.А. Бейнарович

Кандидат технических наук, доцент кафедры электроники

и автоматики физических установок СГТА

В.Б. Терехин

© ГОУ ВПО «Томский политехнический университет», 2012

© Чернышев А.Ю., Чернышев И.А., 2012

© Оформление. Издательство Томского политехнического университета, 2012

Пример 4.2. Для короткозамкнутого асинхронного двигателя типа АИР90L2 определить параметры Т-образной схемы замещения. Двигатель имеет следующие технические данные [4]: Здесь ЕНТЕРНЕТ.

• номинальная мощность кВт;

• номинальное фазное напряжение В;

• синхронная частота вращения об/мин;

• номинальное скольжение о. е.;

• коэффициент полезного действия электродвигателя в режиме номинальной мощности (100%-я нагрузка) %;

• коэффициент мощности в режиме номинальной мощности о. е.;

• кратность пускового тока о. е.;

• кратность пускового момента о. е.;

• кратность максимального момента о. е.;

• кратность минимального момента о. е.

Решение

(Для определения параметров схемы замещения асинхронного двигателя можно воспользоваться математической системой Mathcad и программой ИДЗ 2200.xmcd)

Найдем ток холостого хода асинхронного двигателя

А,

где А – номинальный ток статора двигателя;

– число фаз асинхронного двигателя;

А – ток статора двигателя при частичной загрузке;

о. е. – коэффициент мощности при частичной загрузке (см. рис. 4.6);

о. е. – КПД при частичной загрузке;

о. е. – коэффициент загрузки двигателя.

Критическое скольжение

о.е.

Значение коэффициента , согласно [7], находится в диапазоне 0,6 2,5. Принимаем  =1,3.

Определим коэффициенты:

;

.

Активное сопротивление ротора, приведенное к обмотке статора асинхронного двигателя,

Ом.

Активное сопротивление обмотки статора

Ом.

Определим параметр , который позволяет найти индуктивное сопротивление короткого замыкания :

.

Тогда

.

Индуктивное сопротивление рассеяния фазы роторной обмотки, приведенное к статорной, может быть рассчитано по уравнению

Ом.

Индуктивное сопротивление рассеяния фазы статорной обмотки может быть определено по следующему выражению:

Ом.

ЭДС ветви намагничивания , наведенная потоком воздушного зазора в обмотке статора в номинальном режиме, равна

В,

тогда индуктивное сопротивление контура намагничивания

Ом.

В том случае если параметры схемы замещения асинхронного двигателя определены по его каталожным данным, необходимо их проверить, рассчитав статические электромеханические и механические характеристики двигателя, сравнив их контрольные точки с паспортными данными двигателя, а также рассчитать переходные процессы прямого пуска двигателя, убедившись в его устойчивости.

4.2.5. Составление динамической модели асинхронного

двигателя в неподвижной системе координат

Для окончательной проверки правильности определения параметров схемы замещения асинхронного двигателя рассчитаем переходные процессы пуска двигателя прямым включением в сеть с учетом электромагнитных процессов.

Исходная система дифференциальных уравнений, описывающая асинхронный двигатель с короткозамкнутым ротором в векторной форме записи в неподвижной системе координат , имеет вид:

(4.35)

(4.36)

(4.37)

(4.38)

где – вектор напряжения обмотки статора в неподвижной системе координат;

– вектор тока обмотки статора в неподвижной системе координат;

– вектор потокосцепления обмотки статора в неподвижной системе координат;

– вектор тока обмотки ротора в неподвижной системе координат;

– вектор потокосцепления обмотки статора в неподвижной системе координат;

– вектор потокосцепления обмотки ротора в неподвижной системе координат;

– индуктивность обмотки статора, равная индуктивности рассеяния обмотки статора и индуктивности от главного поля;

– индуктивность обмотки ротора, приведенная к обмотке статора, равная индуктивности рассеяния обмотки ротора приведенной к обмотке статора и индуктивности от главного поля;

– индуктивность от главного поля (контура намагничивания), создаваемая суммарным действием токов статора;

– электрическая скорость вращения ротора.

Электромагнитный момент асинхронного двигателя можно выразить через любую пару векторов [2, 3] . При решении данной задачи наиболее целесообразно определять электромагнитный момент асинхронного двигателя через векторы тока статора и потокосцепления ротора

(4.39)

где – вектор потокосцепления, комплексно сопряженный с вектором потокосцепления обмотки ротора .

Электромеханические процессы в электроприводе описываются уравнением движения. Для случая

, (4.40)

где – электромагнитный момент, развиваемый асинхронным двигателем;

– момент сопротивления механизма, приведенный к валу двигателя;

– момент инерции электропривода, приведенный к валу двигателя, .

Преобразуем систему уравнений (4.35) – (4.38), оставив в качестве переменных, описывающих асинхронный двигатель, пространственные векторы тока статора и потокосцепления ротора , исключив промежуточные переменные и .

Систему уравнений (4.35) – (4.38), содержащую четыре переменных вектора состояния , , , можно преобразовать в два уравнения, содержащих два переменных вектора и , входящих в принятое выражение электромагнитного момента асинхронного двигателя (4.39).

Введем следующие обозначения:

; ; ; . (4.49)

Упростим уравнения (4.42) и (4.48), подставив в них обозначения (4.49), получим

, (4.50)

. (4.51)

Преобразуем уравнения (4.50) и (4.51) из векторной формы записи в скалярную, записав их через проекции векторов на оси неподвижной правой декартовой системы координат. Пространственные векторы в этом случае представляются следующим образом:

; ; .

Графическое разложение векторов на их составляющие по осям представлено на рис. 4. 13, там же показано, что умножение вектора на равносильно его повороту на

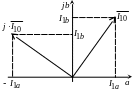
Рис. 4.13. Представление вектора тока в осях

Тогда уравнения (4.50) и (4.51) представляются в следующем виде:

; (4.52)

; (4.53)

; (4.54)

, (4.55)

где – напряжение обмотки статора асинхронного двигателя, ориентированная вдоль оси неподвижной декартовой системы координат , В;

– напряжение обмотки статора асинхронного двигателя, ориентированная вдоль оси неподвижной декартовой системы координат , В;

– амплитудное значение фазного напряжения обмотки статора, В;

– действующее значение фазного напряжения обмотки статора, В;

– составляющая вектора тока обмотки статора, ориентированная вдоль оси неподвижной системы координат, А;

– составляющая вектора тока обмотки статора, ориентированная вдоль оси неподвижной системы координат, А;

– составляющая вектора потокосцепления обмотки ротора, ориентированная вдоль оси неподвижной системы координат, Вб;

– составляющая вектора потокосцепления обмотки ротора, ориентированная вдоль оси неподвижной системы координат, Вб.

Уравнения (4.52) – (4.55) после некоторых преобразований в операторной форме записи преобразуются к виду

; (4.56)

; (4.57)

; (4.58)

; (4.59)

Уравнение электромагнитного момента (4.39) в развернутом виде:

; (4.60)

Уравнение движения (4.40) в операторной форме записи имеет следующий вид:

, (4.61)

где – эквивалентная электромагнитная постоянная времени.

Уравнение движения (4.61) записано в скалярном виде. Это возможно в том случае, если характер нагрузки (активная или реактивная) будет учитываться в программе расчета переходных режимов асинхронного электропривода.

Структурная схема динамической модели короткозамкнутого асинхронного электродвигателя в неподвижной системе координат , соответствующая уравнениям (4.56) – (4.61) приведена на рис 4.14.

Анализ динамических процессов преобразования энергии в асинхронном двигателе представляет собой сложную задачу в связи с существенной нелинейностью уравнений, описывающих асинхронный двигатель, обусловленной произведением переменных. Поэтому исследование динамических характеристик асинхронного двигателя целесообразно вести с применением средств вычислительной техники.

Пример 4.4. Для короткозамкнутого асинхронного двигателя типа АИР90L2 рассчитать и построить переходные процессы скорости, момента, тока статора, а также динамическую механическую характеристику. Основные параметры двигателя и его схемы замещения:

• номинальная мощность двигателя кВт;

• номинальное фазное напряжение ;

• номинальная скорость двигателя ;

• номинальный ток обмотки статора ;

• активное сопротивление фазы обмотки статора Ом;

• индуктивное сопротивление рассеяния фазы обмотки статора Ом;

• активное сопротивление ротора, приведенное к обмотке статора, Ом;

• индуктивное сопротивление рассеяния фазы обмотки ротора, приведенное к обмотке статора, Ом;

• индуктивное сопротивление контура намагничивания, 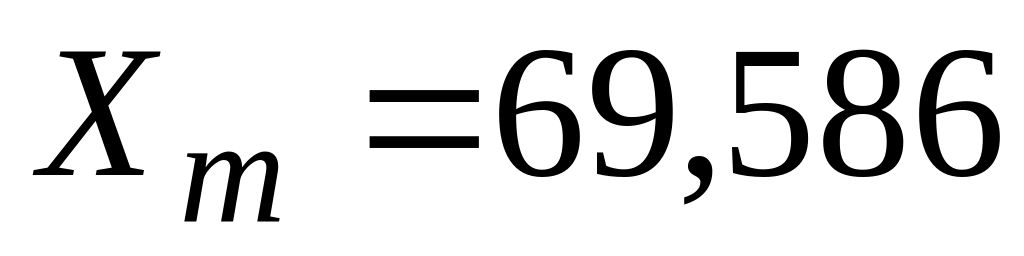Ом.

• кратность пускового тока о. е.;

• кратность максимального момента о. е.;

• кратность минимального момента о. е.;

• момент инерции двигателя .

Решение. Динамическую модель асинхронного двигателя составим в соответствии с его структурной схемой, приведенной на рис. 4.14. Моделирование асинхронного двигателя будем производить в абсолютных единицах, так как современные программные средства для численных вычислений, расчетов и математического моделирования, например, MATLAB позволяют автоматически устанавливать масштаб моделирования независимо от мощности двигателя или его параметров.

Найдем дополнительные параметры структурной схемы в соответствии с принятыми обозначениями (4.49):

Индуктивность рассеяния обмотки статора

Гн.

Индуктивность рассеяния обмотки ротора, приведенная к обмотке статора

Гн.

Индуктивность контура намагничивания

Гн.

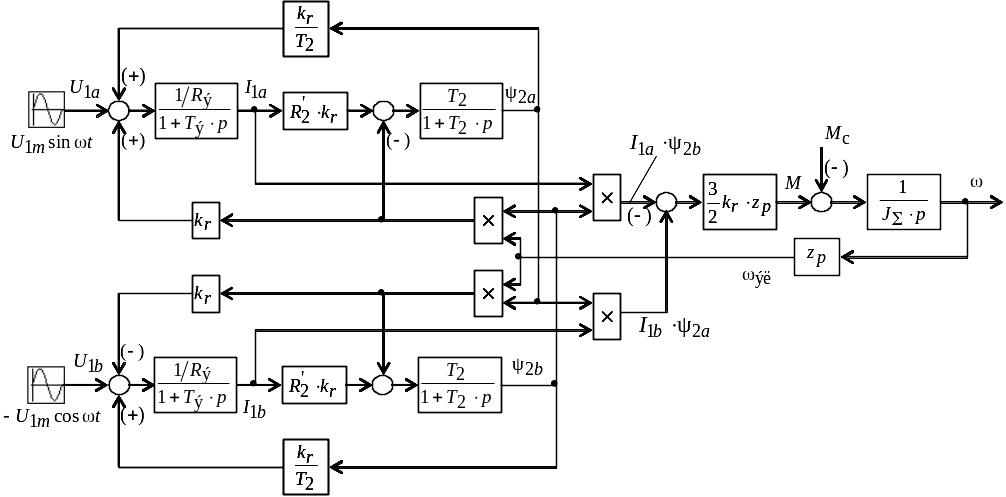
Рис 4.14. Структурная схема короткозамкнутого асинхронного двигателя в неподвижной системе координат a, jb

Индуктивность обмотки статора

Гн.

Индуктивность обмотки ротора

Гн.

Коэффициент

о.е.

Эквивалентное активное сопротивление

Ом.

Эквивалентная индуктивность

Гн.

Эквивалентная индуктивная постоянная времени

c.

Индуктивная постоянная времени обмотки ротора

с.

Схема имитационной модели короткозамкнутого асинхронного двигателя, составленная в неподвижной системе координат a, jb в программной среде MATLAB, приведена на рис. 4.15.

Графики переходных процессов скорости момента и тока статора при пуске асинхронного двигателя прямым включением в сеть приведены на рис. 4.16 – 4.18.

Анализ графиков показывает, что при отработке переходных процессов без нагрузки (режим идеального холостого хода) асинхронный двигатель разогнался до синхронной скорости , его электромагнитный момент установился равным нулю, а ток статора двигателя в установившемся режиме незначительно отличается от тока статора холостого хода статических характеристик ( А):

А,

где – амплитудное значение тока статора холостого хода.

Рис. 4.15. Схема имитационной модели короткозамкнутого асинхронного двигателя

в неподвижной системе координат a, jb

В момент времени с на валу двигателя произведен наброс нагрузки, равный номинальному моменту двигателя .

При отработке возмущающего воздействия установившаяся скорость двигателя уменьшилась до номинальной скорости , электромагнитный момент в установившемся режиме стал равен статическому моменту на валу двигателя , а ток статора двигателя незначительно отличается от номинального тока статора (6,113 А) статических характеристик двигателя:

А,

где – амплитудное значение номинального тока статора.

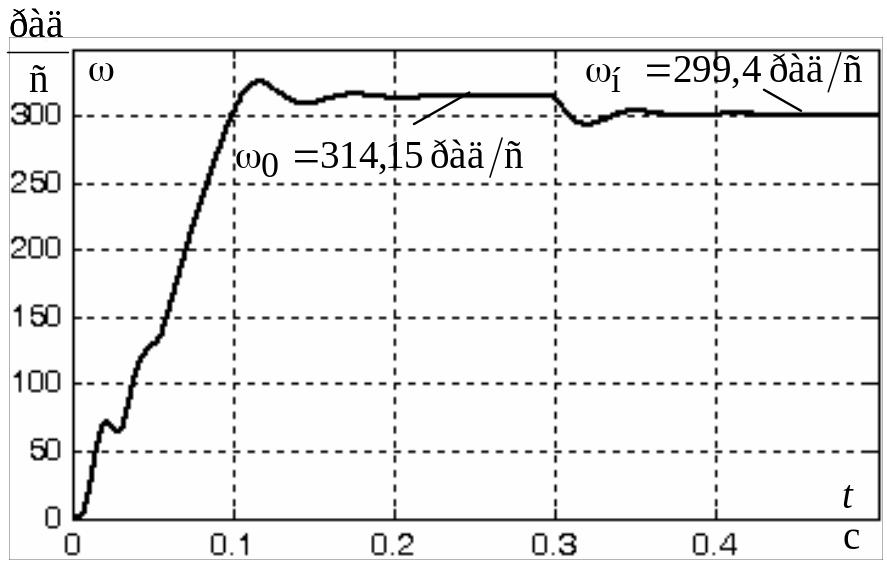
Рис. 4.16. График переходного процесса скорости

при пуске асинхронного двигателя прямым включением в сеть

Рис. 4.17. График переходного процесса момента

при пуске асинхронного двигателя прямым включением в сеть

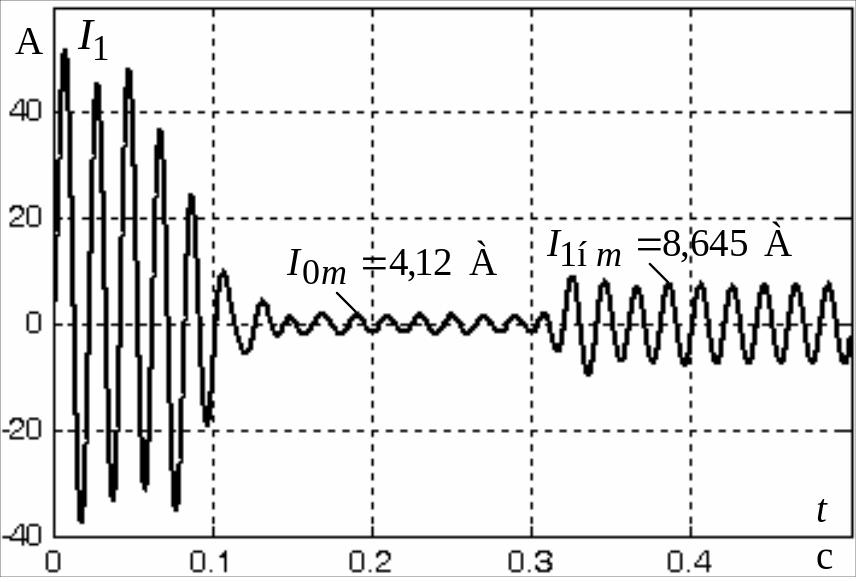
Рис. 4.18. График переходного процесса тока статора

при пуске асинхронного двигателя прямым включением в сеть

По результатам расчета переходных процессов на рис. 4.19 построена динамическая механическая характеристика асинхронного двигателя при пуске прямым включением в сеть с последующим набросом нагрузки до .

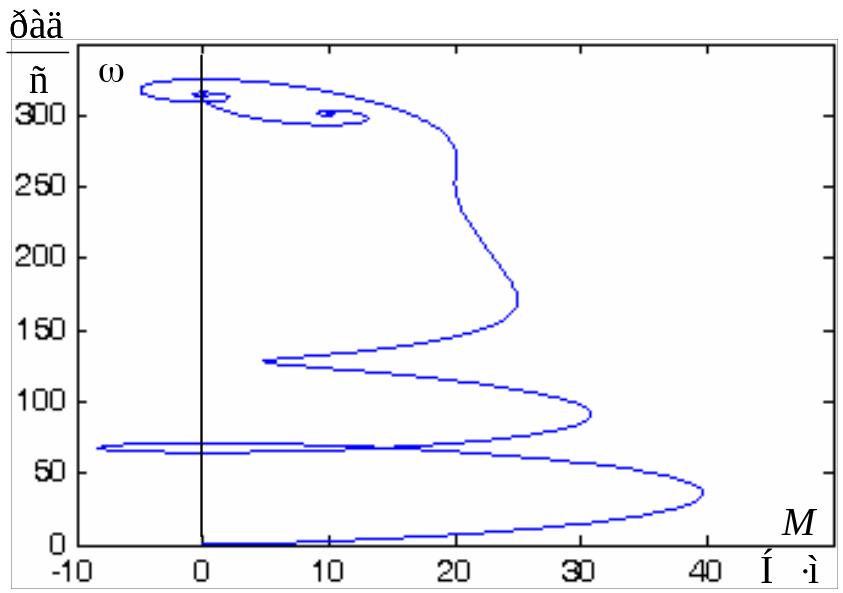
Рис. 4.19. Динамическая механическая характеристика асинхронного

двигателя при пуске прямым включением в сеть

Анализ динамической механической характеристики асинхронного двигателя показывает, что максимальный ударный момент при пуске превышает номинальный момент статической механической характеристики в 4 раза и может достичь недопустимо больших по механической прочности значений, поэтому желательно в дальнейшем исследовать переходные режимы пуска асинхронного двигателя от тиристорных пусковых устройств.

Выводы.

• Анализ графиков переходных процессов тока, скорости и момента показал, что асинхронный электродвигатель с найденными параметрами схемы замещения является устойчивым звеном и эти параметры можно использовать в дальнейшем при исследовании и настройке систем регулирования с применением данного двигателя.

• Имитационная модель, созданная в программной среде MATLAB адекватно отображает переходные режимы, в короткозамкнутом асинхронном двигателе и может быть использована при исследовании его динамических процессов.