Часть 2

С1. Решите уравнение и найдите корни, принадлежащие отрезку .

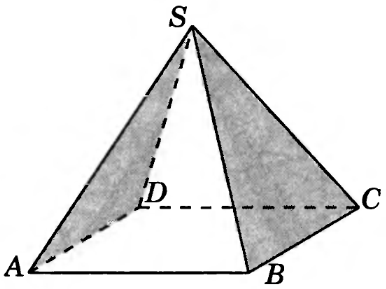
С2. В правильной четырехугольной пирамиде , все ребра которой равны 1, найдите косинус угла между плоскостями и .

С3. Решите систему неравенств

С4. Площадь трапеции равна , а одно из оснований трапеции вдвое больше другого. Диагонали пересекаются в точке , отрезки, соединяющие середину основания с вершинами и , пересекаются с диагоналями трапеции в точках и соответственно. Найдите площадь четырехугольника .

С5. Найдите все значения , при каждом из которых система

имеет единственное решение.

С6. Бесконечная арифметическая прогрессия, состоящая из различных натуральных чисел, первый член которой меньше , не содержит ни одного числа вида . Какое наименьшее значение может принимать сумма со второго по пятнадцатый член этой прогрессии?

ВАРИАНТ 4

Часть 1

В1. В квартире, где проживает Алексей, установлен прибор учёта расхода холодной воды (счётчик). 1 апреля счётчик показывал расход 188 куб.м воды, а 1 мая — 202 куб.м. Какую сумму должен заплатить Алексей за холодную воду за апрель, если цена 1 куб.м холодной воды составляет 10 руб. 90 коп.? Ответ дайте в рублях.

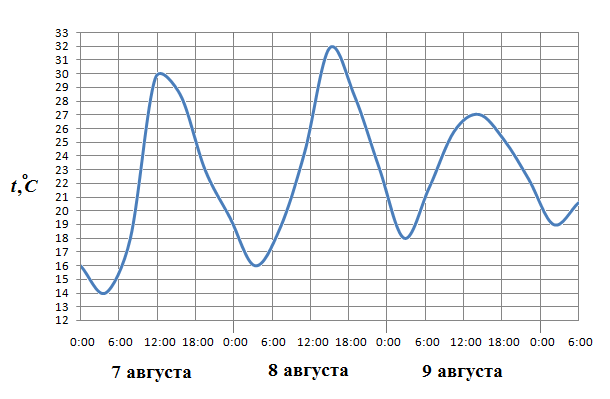
В2. На рисунке показано изменение температуры воздуха на протяжении трёх суток. По горизонтали указывается дата и время, по вертикали — значение температуры в градусах Цельсия. Определите по рисунку разность между наибольшей и наименьшей температурами воздуха 7 августа. Ответ дайте в градусах Цельсия.

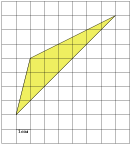
В3. Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1 см 1 см (см. рис.). Ответ дайте в квадратных сантиметрах.

В4. Независимая экспертная лаборатория определяет рейтинг бытовых приборов на основе коэффициента ценности, равного 0,01 средней цены , показателей функциональности , качества и дизайна . Каждый из показателей оценивается целым числом от 0 до 4. Итоговый рейтинг вычисляется по формуле . В таблице даны средняя цена и оценки каждого показателя для нескольких моделей электрических мясорубок. Определите наивысший рейтинг представленных в таблице моделей электрических мясорубок.

Модель мясорубки	Средняя цена	Функциональность	Качество	Дизайн
А	4900	0	3	4
Б	5100	2	3	0
В	3600	0	1	1
Г	6000	4	3	2

В5. Найдите корень уравнения .

В6. В треугольнике ABC угол C равен , высота CH равна 12, . Найдите .

В7. Найдите , если .

В8. На рисунке изображен график – производной функции , определенной на интервале . Найдите количество точек минимума функции , принадлежащих отрезку .

В9. В правильной треугольной пирамиде – середина ребра , – вершина. Известно, что , а площадь боковой поверхности равна 168 . Найдите длину отрезка .

В10. На олимпиаде по физике участников рассаживают по трём аудиториям. В первых двух по 100 человек, оставшихся проводят в запасную аудиторию в другом корпусе. При подсчёте выяснилось, что всего было 400 участников. Найдите вероятность того, что случайно выбранный участник писал олимпиаду в запасной аудитории.

В11. Объем куба равен 90. Найдите объем четырехугольной пирамиды, основанием которой является грань куба, а вершиной — центр куба.

В12. К источнику с ЭДС В и внутренним сопротивлением  Ом, хотят подключить нагрузку с сопротивлением R Ом. Напряжение на этой нагрузке, выражаемое в вольтах, задается формулой . При каком наименьшем значении сопротивления нагрузки напряжение на ней будет не менее 90 В? Ответ выразите в Омах.

В13. Расстояние между пристанями A и B равно 140 км. Из A в B по течению реки отправился плот, а через 1 час вслед за ним отправилась яхта, которая, прибыв в пункт B, тотчас повернула обратно и возвратилась в A. К этому времени плот прошел 52 км. Найдите скорость яхты в неподвижной воде, если скорость течения реки равна 4 км/ч. Ответ дайте в км/ч.

В14. Найдите наименьшее значение функции на отрезке .