Часть 2

С1. Решите уравнение и найдите корни, принадлежащие отрезку .

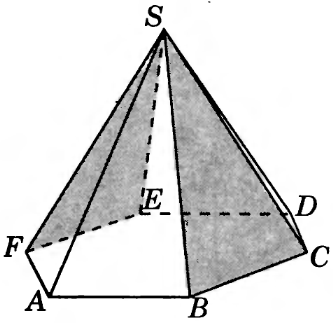
С2. В правильной шестиугольной пирамиде , стороны основания которой равны 1, а боковые ребра равны 2, найдите косинус угла между плоскостями и .

С3. Решите систему неравенств

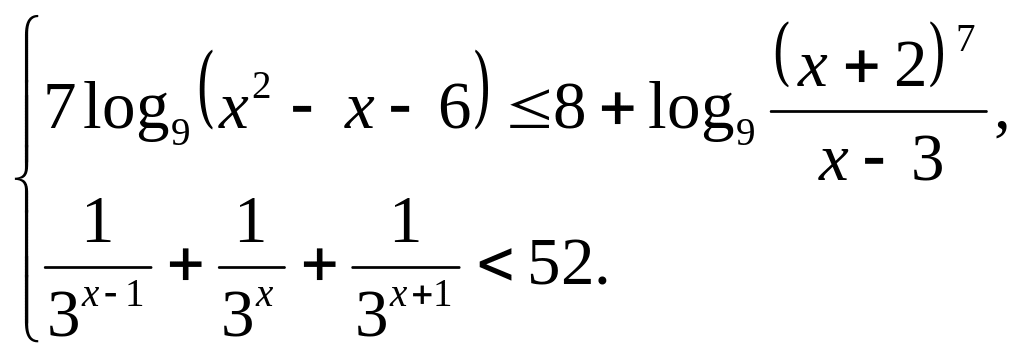
С4. Дана трапеция , основания которой , , . Окружность, касающаяся прямых и , касается стороны в точке . Найдите длину отрезка .

С5. Найдите все значения , при каждом из которых система

имеет единственное решение.

С6. Бесконечная арифметическая прогрессия, состоящая из различных натуральных чисел, первый член которой меньше , не содержит ни одного числа вида . Какое наименьшее значение может принимать сумма первых членов этой прогрессии?

ВАРИАНТ 3

Часть 1

В1. В квартире, где проживает Анастасия, установлен прибор учёта расхода холодной воды (счётчик). 1 марта счётчик показывал расход 112 куб.м воды, а 1 апреля — 118 куб.м. Какую сумму должна заплатить Анастасия за холодную воду за март, если цена 1 куб.м холодной воды составляет 13 руб. 40 коп.? Ответ дайте в рублях.

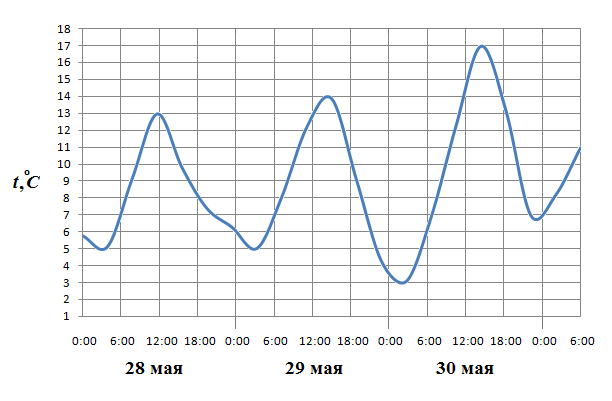
В2. На рисунке показано изменение температуры воздуха на протяжении трёх суток. По горизонтали указывается дата и время, по вертикали — значение температуры в градусах Цельсия. Определите по рисунку разность между наибольшей и наименьшей температурами воздуха 28 мая. Ответ дайте в градусах Цельсия.

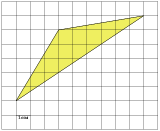
В3. Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1 см 1 см (см. рис.). Ответ дайте в квадратных сантиметрах.

В4. Независимая экспертная лаборатория определяет рейтинг бытовых приборов на основе коэффициента ценности, равного 0,01 средней цены , показателей функциональности , качества и дизайна . Каждый из показателей оценивается целым числом от 0 до 4. Итоговый рейтинг вычисляется по формуле . В таблице даны средняя цена и оценки каждого показателя для нескольких моделей электрических мясорубок. Определите наивысший рейтинг представленных в таблице моделей электрических мясорубок.

Модель мясорубки	Средняя цена	Функциональность	Качество	Дизайн
А	5600	1	3	3
Б	5800	4	2	0
В	5100	2	2	2
Г	5100	3	3	2

В5. Найдите корень уравнения .

В6. В тупоугольном треугольнике ABC , CH  — высота, , . Найдите синус угла ABC.

В7. Найдите , если .

В8. На рисунке изображен график – производной функции , определенной на интервале . Найдите количество точек экстремума функции , принадлежащих отрезку .

В9. В правильной треугольной пирамиде – середина ребра , – вершина. Известно, что , а . Найдите площадь боковой поверхности.

В10. Какова вероятность того, что случайно выбранное натуральное число от 79 до 98 делится на 2?

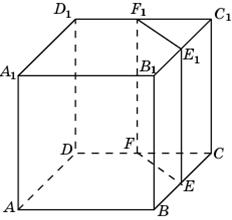
В11. Объем куба равен 60. Найдите объем треугольной призмы, отсекаемой от него плоскостью, проходящей через середины двух ребер, выходящих из одной вершины и параллельной третьему ребру, выходящему из этой же вершины.

В12. Коэффициент полезного действия (КПД) кормозапарника равен отношению количества теплоты, затраченного на нагревание воды массой (в килограммах) от температуры до температуры (в градусах Цельсия) к количеству теплоты, полученному от сжигания дров массы  кг. Он определяется формулой , где Дж/(кг·К) — теплоемкость воды, Дж/кг – удельная теплота сгорания дров. Определите наименьшее количество дров, которое понадобится сжечь в кормозапарнике, чтобы нагреть кг воды от до кипения, если известно, что КПД кормозапарника не больше . Ответ выразите в килограммах.

В13. Расстояние между городами A и B равно 120 км. Из города A в город B выехал автомобиль, а через 1 час следом за ним со скоростью 80 км/ч выехал мотоциклист, догнал автомобиль в городе C и повернул обратно. Когда он вернулся в A, автомобиль прибыл в B. Найдите расстояние от A до C. Ответ дайте в километрах.

В14. Найдите наибольшее значение функции на отрезке .