2. Выбор конечного элемента

Для дальнейшей работы нам необходимо выбрать конечный элемент. В данной работе отдается предпочтение элементу SOLID 186. Структура этого элемента изображена ниже рис. 3.2.

Рисунок 3.2 - Геометрия структуры элемент SOLID 186

SOLID 186 – это твердый 3d элемент с двадцатью узлами и тремя степенями свободы. Поддерживает пластичность, гиперупругость, напряжение жесткости и большую деформацию.

3. Построение конечно-элементной модели

Для построения конечно-элементной модели необходимо выбрать конечный элемент, задать свойства материала и построить сетку.

Эти характеристики необходимо ввести в меню Preprocessor->Material Prop->MaterialModels. Далее для построения сетки используется команда Preprocessor->Meshing->Mesh->Volumes->Free. Она отвечает за построение произвольной сетки.

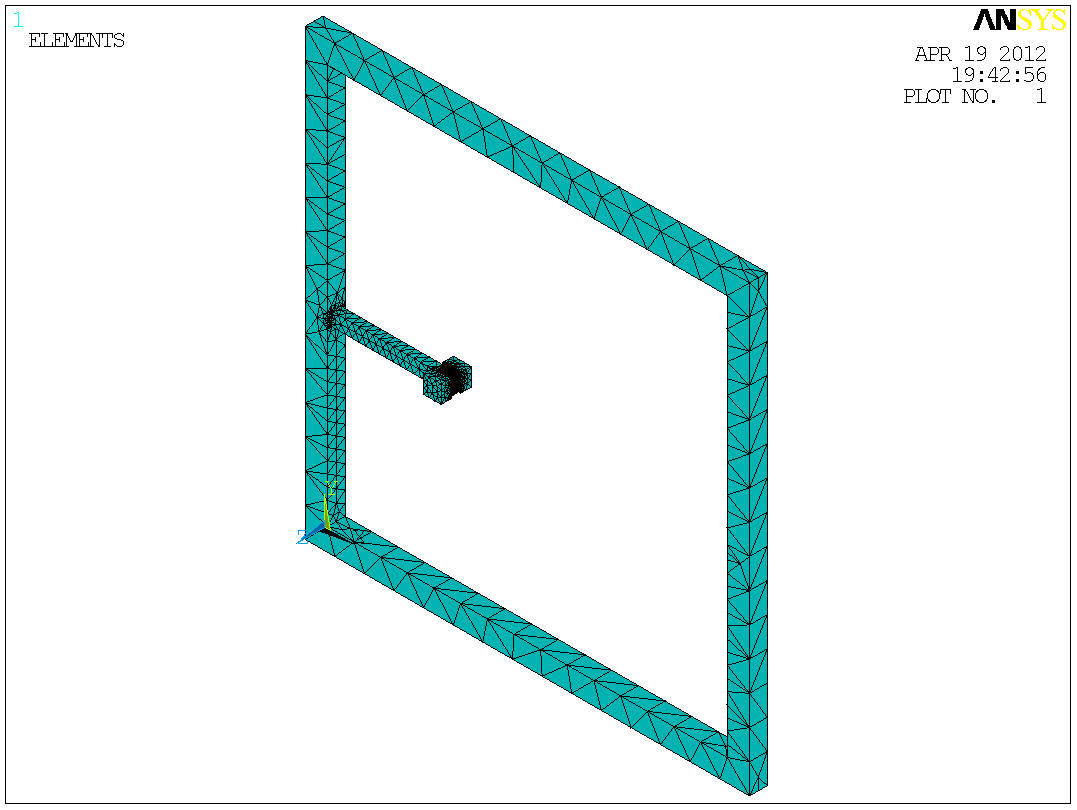
Рисунок 3.3 – Построение конечно-элементной модели

Выводы

В этой главе было рассмотрена технология построение 3d модели, выбора конечно элемента и создания конечно-элементой модели в программном комплексе ANSYS ED.

Конечный элемент был выбран таким образом, чтобы на его базе можно было проводить статический и модальный анализы.

4. Выполнение анализов

   1. Статический анализ микроакселерометра

Выполняем статический анализ акселерометра для диапазона от -1g до -100g с шагом 20g. Результаты анализов представлены в таблицах 4.1 – 4.6 и на рисунках 4.1 – 4.3.

Таблица 4.1 – Зависимость смещения от ускорения по оси Y

Ускорение, *g, м/с^2	-1	-20	-40	-60	-80	-100
D(x), м * e-13	3.25	64.9	130	195	260	325
D(y), м * e-13	32.5	651	1300	1950	2600	3250
D(z), м * e-13	0.0589	1.18	2.36	3.53	4.71	5.89
D(Σ), м * e-13	32,7	654	1310	1960	2620	3270

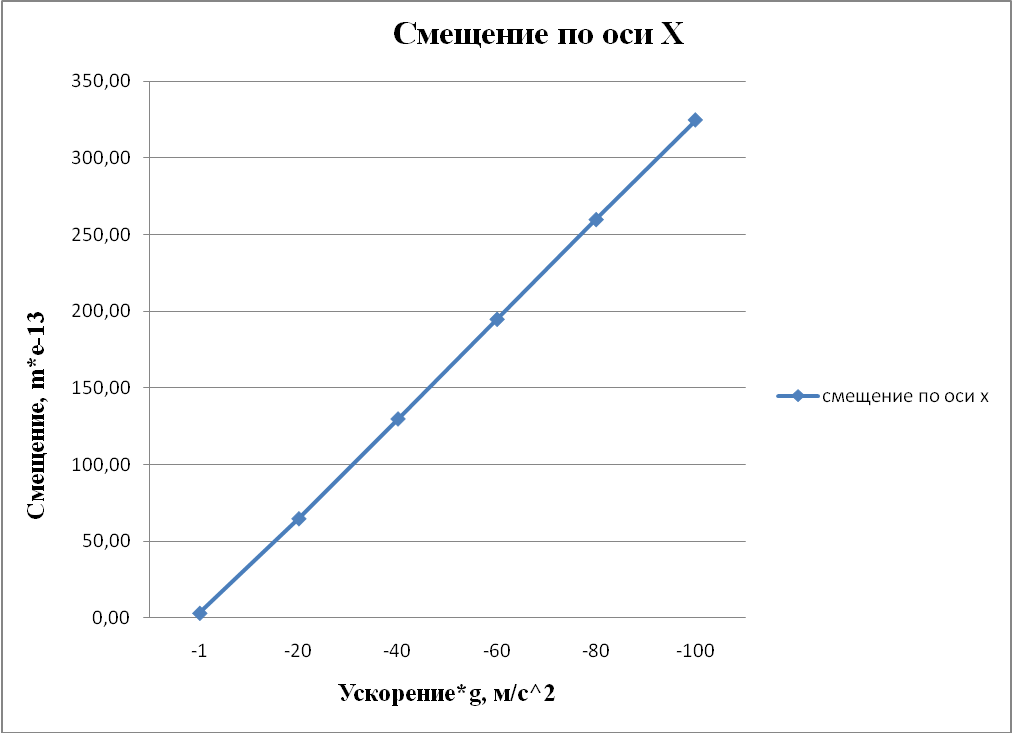
Рисунок 4.1 - Смещение по оси Х. Статический анализ при ускорении по оси Y

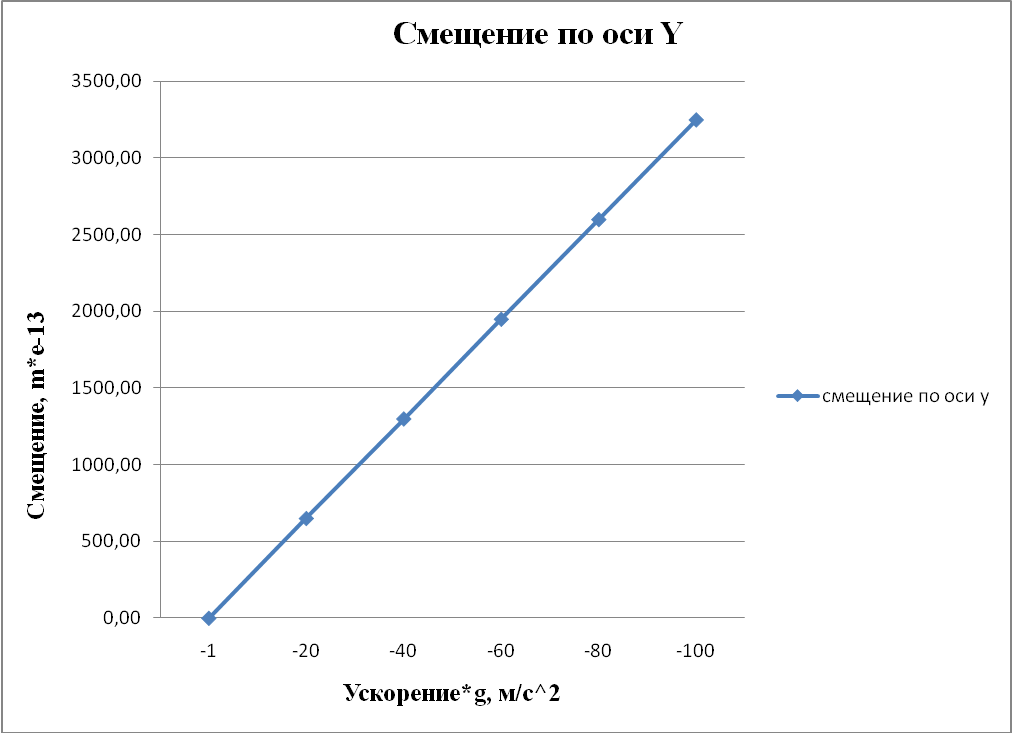
Рисунок 4.2 – Смещение по оси Y. Статический анализ при ускорении по оси Y

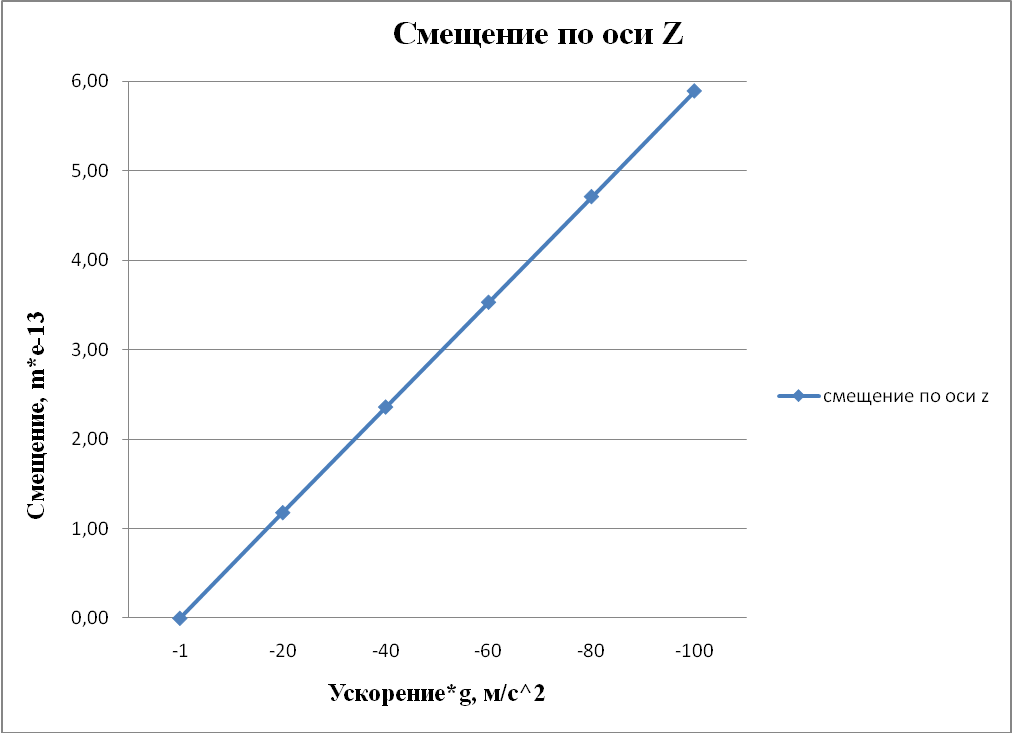
Рисунок 4.3 – Смещение по оси Z. Статический анализ при ускорении по оси Y

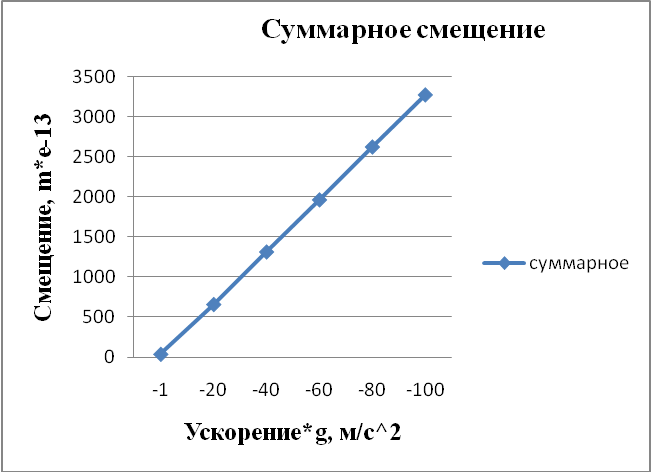
Рисунок 4.4 - Суммарное смещение. Статический анализ при ускорении по оси Y

Таблица 4.2 – Зависимость напряжения от ускорения по оси Y

Ускорение, *g, м,c^2	-1	-20	-40	-60	-80	-100
Напряжение, Па	562.574	11251.5	22503	33754.4	45005.9	56257.4

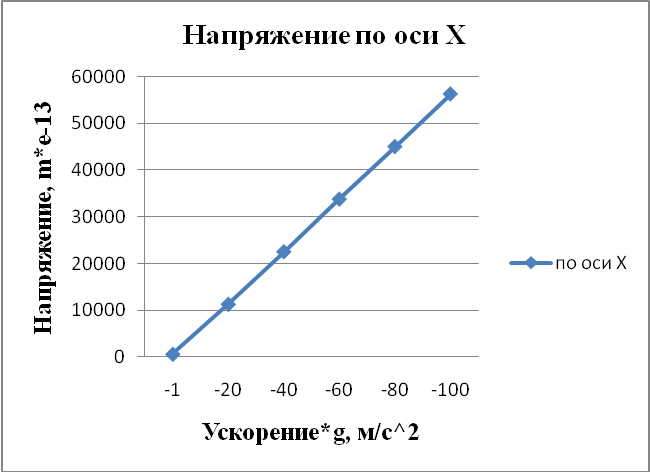
Рисунок 4.5 - Напряжение по Х. Ускорение только по оси Y

Далее построим графики зависимости чувствительности от ускорения. Чувствительность рассчитывается как отношение смещения к ускорению. Результаты расчетов отображены в таблице 4.3 и на рисунке 4.6.

Таблица 4.3 – Зависимость чувствительности от ускорения по оси Y

Ускорение, *g, м,c^2	-1	-20	-40	-60	-80	-100
Чувствительность, с^2	3,336	3,336	3,341	3,333	3,341	3,336

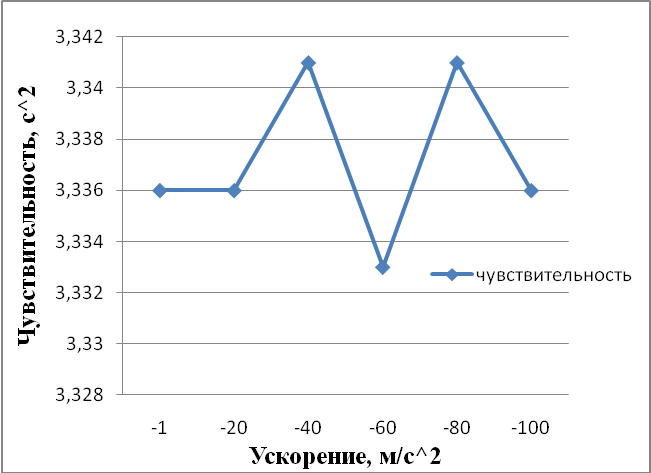
Рисунок. 4.6 - Чувствительность по суммарному смещению. Ускорение приложено только по оси Y

Приложим теперь ускорение по всем осям. Значения ускорения по осям Х и Z будет составлять 0,02 от значения ускорения по оси Y. Результаты показаны в таблицах 4.4 – 4.6 и на рисунках 4.7 – 4.12.

Таблица 4.4 – Зависимость смещения от ускорения по всем осям

Ускорение, *g, м/с^2	-1	-20	-40	-60	-80	-100
D(x), м * e-13	3.49	6.98	140	209	279	349
D(y), м * e-13	32.5	651	1300	1950	2600	3250
D(z), м * e-13	1.42	28.5	56.9	85.4	114	142
D(Σ), м * e-13	32,7	655	1310	1960	2620	3270

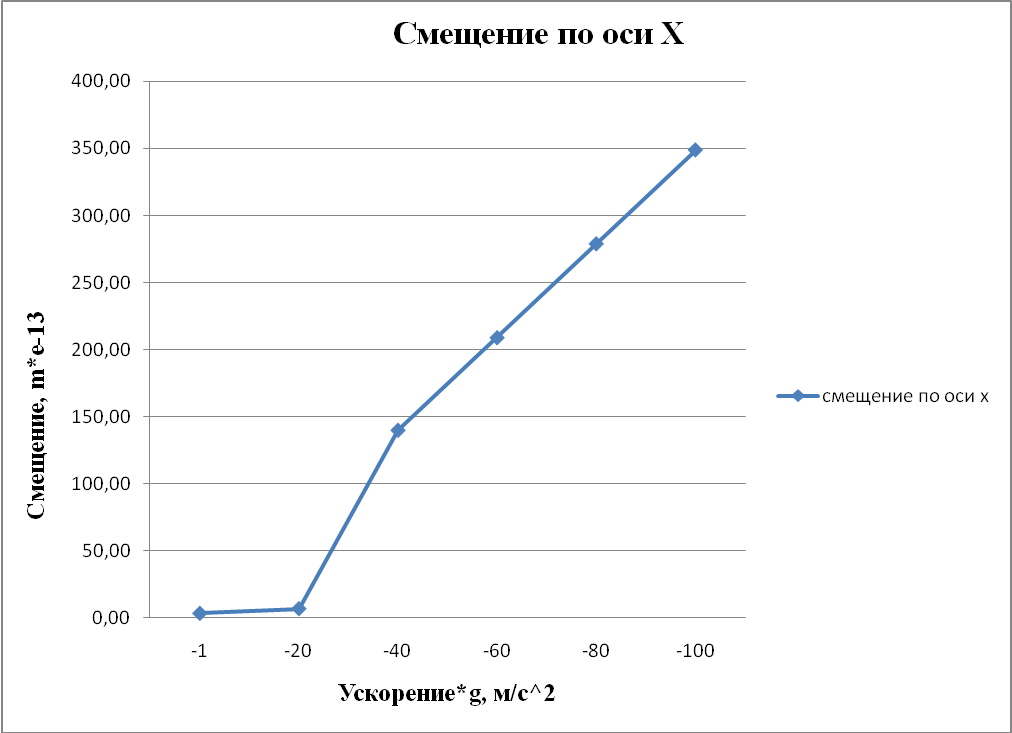
Рисунок 4.7 - Смещение по оси Х. Статический анализ при ускорении по всем осям

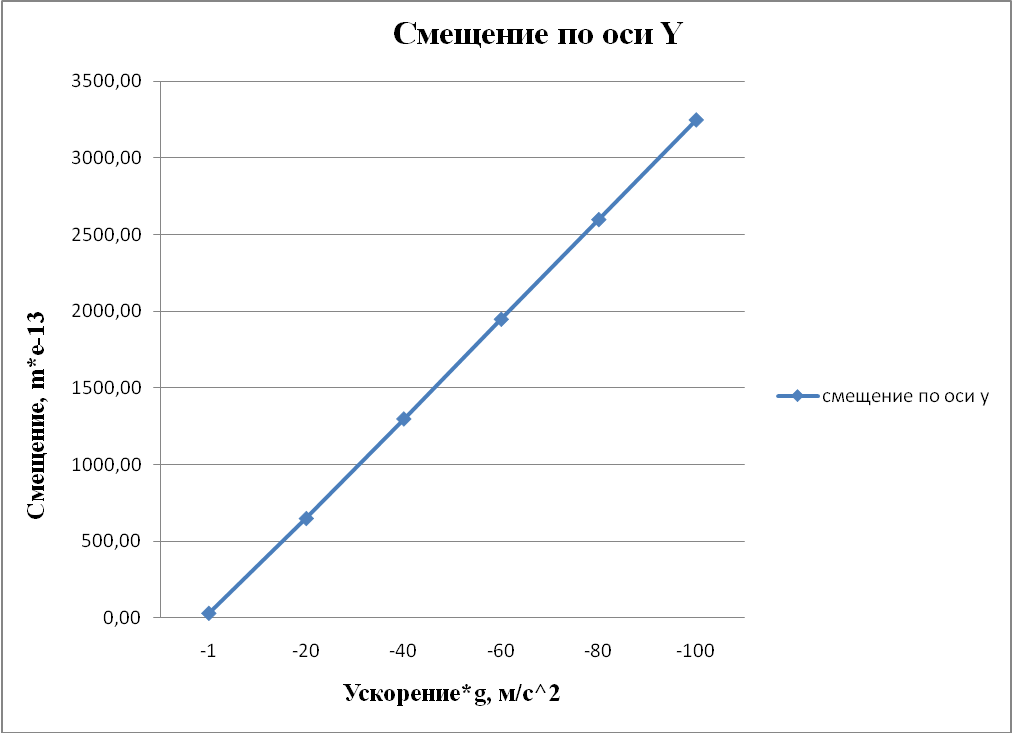
Рисунок 4.8 - Смещение по оси Y. Статический анализ при ускорении по всем осям

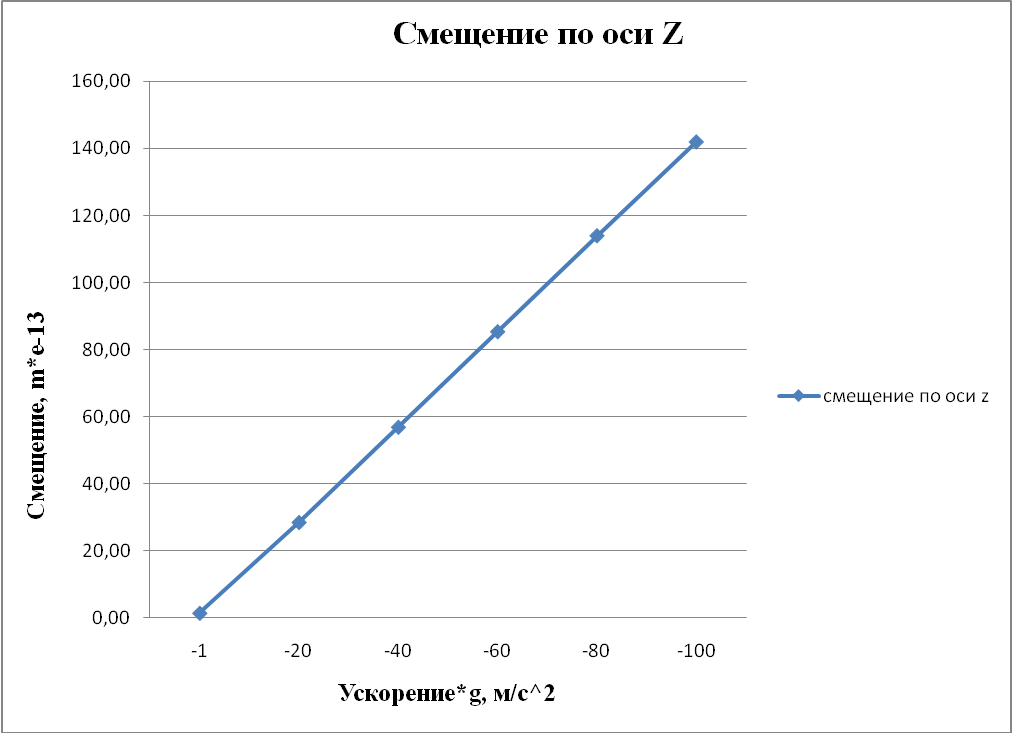
Рисунок 4.9 - Смещение по оси Z. Статический анализ при ускорении по всем осям

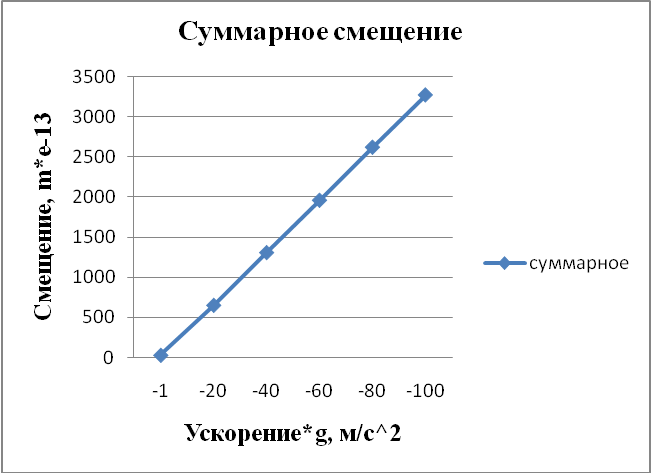
Рисунок 4.10 - Суммарное смещение. Статический анализ при ускорении по всем осям

Таблица 4.5 – Зависимость напряжения от ускорения по всем осям

Ускорение, *g, м,c^2	-1	-20	-40	-60	-80	-100
Напряжение, Па	547,266	10945,3	21890,6	32836	43781,3	54726,6

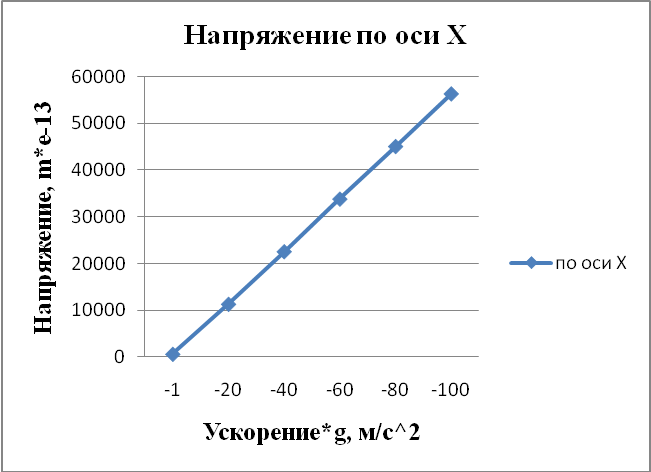
Рисунок 4.11 - Напряжение по Х. Ускорение по всем осям

Таблица 4.6 – Зависимость чувствительности от ускорения по всем осям

Ускорение, *g, м,c^2	-1	-20	-40	-60	-80	-100
Чувствительность, с^2	3,336	3,342	3,341	3,333	3,341	3,336

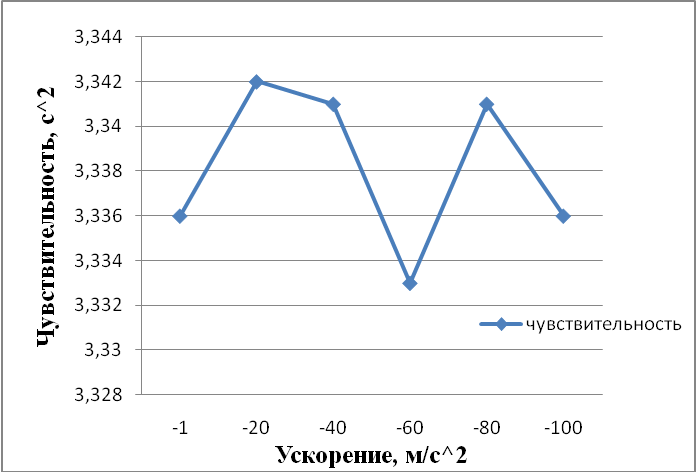
Рисунок. 4.12 - Чувствительность по суммарному смещению. Ускорение приложено только по всем осям