Класифікація систем

Системи можна класифікувати по кільком ознакам:

1) по числу компонентів системи поділяються на:

• однокомпонентні,

• двохкомпонентні,

• трьохкомпонентні,

• багатокомпонентні;

2) по числу фаз системи поділяються на:

• однофазні,

• двохфазні,

• трьохфазні,

• чотирьохфазні.

3) по числу ступенів свободи системи поділяються на:

• інваріантні (С = 0),

• моноваріантні (С = 1),

• двоваріантні (С = 2),

• поліваріантні (С > 2).

Правило фаз Гіббса широко застосовується для аналізу фазового стану системи.

3.2 Застосування правила фаз Гіббса до однокомпонентних систем. Загальний принцип побудови діаграм

Для однокомпонентних систем правило фаз (3.6) приймає вигляд

С = К – Ф +2 = 1 – Ф + 2 = 3 –Ф. (3.6)

Якщо мінімальне число ступенів свободи (Сmin) дорівнює нулю (система інваріантна), то, згідно з (3.6), число фаз Ф = 3. У рівноважній однокомпонентній системі можуть співіснувати максимально три фази (т, р, г). Максимальне число ступенів свободи (Сmax) система має при мінімальному числу фаз, що не може бути менше одиниці. Отже, Cmax = 1 – 1 + 2 = 2. Цими ступенями свободи є тиск і температура.

Графічне зображення залежності тиску Р від температури Т (чи Р від складу і Т від складу) називають діаграмою стану. Аналіз діаграм стану дозволяє визначити число фаз, межі їхнього існування, характер взаємодії компонентів, наявність знову утворених хімічних сполук і їхній склад. Діаграми дозволяють проводити аналіз без виділення індивідуальних компонентів.

Такий метод фізико-хімічного аналізу багатокомпонентних систем був запропонований Н. С. Курнаковим (1912 – 1914). В основі аналізу діаграм стану, як показав Н. С. Курнаков, лежать два загальних положення: принцип безперервності і принцип відповідності. Відповідно до принципу безперервності, при безупинній зміні параметрів властивості окремих фаз змінюються також безупинно. Властивості системи в цілому змінюються безупинно доти, поки не зміниться число чи природа фаз, після чого властивості системи змінюються стрибкоподібно. Відповідно до принципу відповідності, на діаграмі стану кожній фазі відповідає частина площини, що називають полем фази. Поле фази зображує область існування фази у визначеному стані (т, р, г). Лінії перетинання площин характеризують рівноважний стан т р; р г; т г. Точка на діаграмі стану (фігуративна точка) показує значення параметрів, що характеризують даний стан системи.

Діаграма стану води

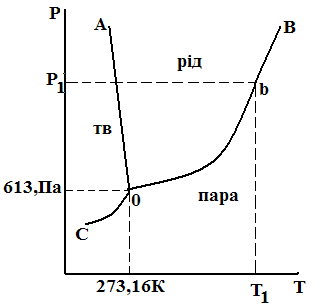
Рисунок 3.1 – Діаграма стану води

На рис. 3.1 приведена діаграма стану води, на якій маються три поля: льоду (т), рідини (р) і пари (п). У межах кожного поля можна довільно змінювати температуру і тиск без зміни числа фаз, тому що при Ф = 1 число ступенів свободи С = 1 – 1 + 2 = 2. Криві, ОА, ОВ і ОС характеризують ті значення Р і Т, при яких у системі маються в рівновазі дві фази. Кожна з кривих показує залежність температури фазового переходу від зовнішнього тиску. Лінія ОА показує залежність температури замерзання води від зовнішнього тиску. Лінія ОВ показує залежність температури кипіння води від зовнішнього тиску. Лінія ОС показує залежність температури сублімації льоду від зовнішнього тиску.

Система, задана точкою на будь-якій кривій, моноваріантна, тобто має один ступінь свободи (С = 3 – 2 = 1). Отже, довільно можна змінювати чи тиск, чи температуру. Другий параметр змінюється в залежності від першого. Наприклад, при обраній температурі T1 (рис. 3.1) рівновага ж п може існувати тільки при тиску P1 (точка b). Якщо при Т1 довільно змінити тиск, то система з двохфазної перейде в однофазну.

Точка 0 на діаграмі відповідає системі, в якій існують три фази (т, р, п). У цьому випадку С = 1 – 3 + 2 = 0 (система інваріантна). У такому стані система може знаходитися при Т = 273,16 К і тиску Р = 613,3 Па. Точку 0 називають потрійною точкою води. Навіть нескінченно мала зміна одного з параметрів порушує рівновагу і приводить до зникнення однієї чи двох фаз.

Якщо система складається з двох компонентів, а на стан рівноваги впливають такі зовнішні фактори, як температура і тиск, то правило фаз Гіббса виражають рівнянням

С = 2 – Ф + 2 = 4 – Ф. (3.7)

При С = 0 число фаз Ф = 4. Отже, у двохкомпонентній системі число фаз, що одночасно знаходяться в рівновазі не може бути більше чотирьох. Максимальне число ступенів свободи в гомогенній системі (при Ф = 1) дорівнює трьом.

Для металевих систем тиск практично не має істотного впливу на фазову рівновагу, тому для таких систем кількість зовнішніх параметрів n = 1 і правило фаз Гіббса запишеться в такому вигляді:

С = 2 – Ф +1 = 3 – Ф. (3.8)

Таким чином для двокомпонентних металевих систем максимальне число фаз дорівнює трьом, а максимальне число ступенів свободи в гомогенній системі (при Ф = 1) дорівнює двом.

Діаграми стану двокомпонентних систем з твердими фазами одержують експериментально методом термічного аналізу, тому їх називають діаграмами плавкості. Розглянемо деякі з таких діаграм.