3. Формулювання першого закону термодинаміки. Закон Гесса

Перший закон термодинаміки має кілька формулювань:

енергія ізольованої системи є величиною сталою.

Якби енергія ізольованої системи могла збільшуватися без взаємодії з навколишнім середовищем, то можна було б сконструювати вічний двигун першого роду, під яким мається на увазі машина, що робить роботу без витрати енергії. Однак, відповідно до іншого формулювання першого закону,

вічний двигун першого роду неможливий.

Сталість енергії ізольованої системи не виключає можливості переходу одного виду енергії в іншу. При таких переходах енергія не витрачається і не створюється знову. Звідси третє формулювання першого закону, що випливає з закону збереження енергії:

енергія не зникає безслідно і не виникає з нічого, перехід її з одного виду в інший відбувається в строго еквівалентних кількостях.

З закону збереження енергії випливає співвідношення

q = U + W (2.4)

де q – кількість підведеної до системи теплоти; U – збільшення внутрішньої енергії; W – сумарна робота, що вироблена системою.

Рівняння (2.4) є математичним виразом першого закону термодинаміки. З нього випливає, що теплота, підведена до системи, витрачається на зміну внутрішньої енергії і на роботу проти зовнішніх сил.

Тепловим (енергетичним) ефектом процесу Q зветься кількість енергії, що виділяється або поглинається системою в результаті здійснення даного процесу. Як правило, тепловий ефект виміряється в Джоулях і носить ім’я процесу, наприклад – тепловий ефект реакції, або тепловий ефект розчинення. Реакції, які відбуваються з виділенням теплоти (енергії), називають екзотермічними, для них вважають Q > 0; реакції, які відбуваються з поглиненням теп-лоти (енергії), називають ендотермічними для них Q < 0.

Розділ хімічної термодинаміки, присвячений вивченням теплових ефектів хімічних реакцій, називають термохімією. Значення термохімії в металургії дуже велике, якщо врахувати, що теплові ефекти розраховують при укладанні теплових балансів різних металургійних процесів і при дослідженні хімічних рівноваг. Тепловий ефект реакції залежить від природи речовин, що приймають участь в реакції, від температури та умов проведення процесу. Розрізняють ізохорний QV та ізобарний QP теплові ефекти. Відповідно

QV = – U; QP = – ΔH. (2.5)

Тепловий ефект хімічної реакції – це максимальна кількість теплоти, що виділяється або поглинається в необоротному процесі при сталому об’ємі або тиску і за умови, що продукти реакції і вихідні речовини мають однакову температуру і відсутні інші види робіт, крім розширення. Тому в рівняннях (2.5) теплові ефекти QV і Qp (ΔU і ΔH) є функціями стану системи, і звідси випливає термодинамічне обґрунтування закону, встановленого експериментально в 1836 році російським вченим Г. І. Гессом:

тепловий ефект реакції не залежить від шляху процесу, а визначається тільки природою і станом початкових і кінцевих речовин.

4. Другий закон термодинаміки. Ентропія. Термодинамічні потенціали. Третій закон термодинаміки.

Перший закон термодинаміки не дає ніяких вказівок щодо напрямку, у якому можуть відбуватися самодовільні процеси в природі. Для ізольованій системи, наприклад, перший закон вимагає тільки, щоб при всіх процесах енергія системи залишалася сталою. Взагалі, на підставі першого закону не можна з’ясувати, чи будуть в ізольованій системі відбуватися які-небудь процеси.

Другий закон термодинаміки, навпаки, дозволяє передбачати напрямок самодовільних процесів і разом з першим законом встановлює безліч точних кількісних співвідношень між різними макроскопічними параметрами систем у стані термодинамічної рівноваги.

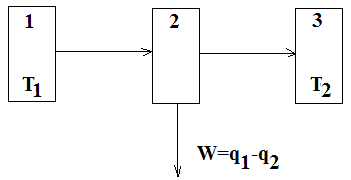
Рисунок 2.4 – Принцип будови теплової машини.

1 – джерело теплоти (тепловіддат-чик); 2 – робоче тіло;

3 – холодильник (теплоприймач).

Першовідкривачем другого закону термодинаміки вважається С. Карно, який досліджував умови перетворення теплоти в роботу (1824) і зробив висновок, що в теплових машинах кількість теплоти, яка одержана від джерела теплоти, не може цілком переходити в роботу; частина її передається холодильнику.

Якщо позначити q₁ теплоту, отриману від джерела енергії, a q₂ – теплоту, віддану холодильнику, то різниця q₁-q₂ являє собою теплоту, перетворену в роботу W. Коефіцієнт корисної дії тут можна виразити рівнянням

. (2.6)

Коефіцієнт корисної дії теплової машини не залежить від природи робочого тіла, а визначається тільки інтервалом температур (теорема Карно— Клаузиуса). Цю теорему зв’язують з формулюванням другого закону термодинаміки, що запропоноване P. Клаузиусом (1850):

теплота не може самодовільно переходити від більш холодного тіла до більш гарячого.

Аналіз формулювань другого закону термодинаміки показує, що усі вони характеризують спрямованість і межу протікання самодовільних процесів, що здійснюються самі собою без витрати енергії, наприклад розширення газу, охолодження гарячого тіла до температури навколишнього середовища і т.п. Визначення умов, при яких відбуваються самодовільні процеси чи настає рівновага, являє великий теоретичний і практичний інтерес.

Другий закон стверджує, що теплоту цілком не можна перетворити в роботу в круговому процесі. Це твердження випливає з природи теплоти і роботи. Імовірність того, що хаотичний тепловий рух молекул цілком перейде в спрямований рух, мізерно мала. Навпроти, спрямований рух молекул може цілком перейти в хаотичний (робота може цілком перейти в теплоту). Газ самодовільно розширюється, але самодовільно не стискується, тому що при стискуванні природний хаотичний рух повинен перетворитися в спрямований рух. Природність хаотичного руху молекул є причиною того, що різні види енергії прагнуть перейти в теплоту, а теплота передається менш нагрітим тілам. Ці процеси самодовільні, природні і необоротні. Таким чином, можна зробити висновок, що протікання самодовільних процесів супроводжується розсіюванням теплової енергії. Щоб процес розсіювання енергії характеризувати кількісно, потрібна була термодинамічна функція, яка показувала б, як змінюється розсіювання енергії при переході системи з одного стану в інший.

Цю функцію ввів P. Клаузиус (1865), назвав ентропією і позначив буквою S.

Для оборотного процесу вона являє собою відношення теплоти процесу до температури, за якої відбувається процес:

. (2.7) Математичний вираз для ентропії в загальному вигляді буде

, (2.8)

де знак нерівності відноситься до необоротних процесів, а знак рівності – до оборотного.

Таким чином, ентропія речовини залежить від її природи і маси, а також від температури. У розрахунках використовують абсолютну стандартну ентропію S⁰₂₉₈.

Стандартною ентропією речовини S⁰₂₉₈ називають абсолютну величину ентропії одного молю даної речовини в стандартних умовах (Р⁰ = 101325 Па, Т = 298 К).

Ентропія є функцією, що визначає можливість здійснення самодовільного процесу в ізольованій системі. Більшість реальних систем не є ізольованими, тому для них не можна застосовувати ентропійний критерій спрямованості процесу. Для закритих систем аналогічними функціями є термодинамічні потенціали: енергія Гельмгольца А (ізохорно-ізотермічний потенціал) і енергія Гіббса G (ізобарно-ізотермічний потенціал). В фізичній хімії енергія Гіббса має більш широке застосування, ніж енергія Гельмгольца, тому що хімічні процеси протікають частіше при постійному тиску, а не при постійному об’ємі.

Енергія Гельмгольца й енергія Гиббса виражаються рівняннями

A = U – TS, (2.9)

G = H – TS. (2.10)

Енергія Гіббса залежить від тиску, а енергія Гельмгольца – від об’єму системи. Абсолютні значення термодинамічних потенціалів невідомі, а для розрахунків використовують звичайно зміни мольних потенціалів (ΔA і ΔG, кДж/моль). В довідниках наведені значення цих термодинамічних функцій речовин в стандартних умовах.

Стандартною енергією Гіббса (Гельмгольца) утворення речовини зветься зміна енергії Гіббса (Гельмгольца) в реакції утворення 1 молю складної речовини з простих речовин в стандартних умовах ( Р⁰ = 101325 Па, Т = 298 К).

ΔG⁰₂₉₈ , кДж/моль,

ΔA⁰₂₉₈ ,кДж/моль.

Для простих речовин в найбільш стабільному стані в стандартних умовах стандартна енергії Гіббса дорівнює нулю.

Доказано, що:

– при наближенні до температури абсолютного нуля величини теплоємностей всіх тіл наближаються до нуля;

– неможливо досягти температури абсолютного нуля;

– при абсолютному нулю температур ентропія ідеального кристала в чистому стані дорівнює нулю.

Всі вищенаведені формулювання є формулюваннями так званого третього закону термодинаміки.