Глава 4. Сложное движение
§3. Сложное движение твердого тела
3º. Угловая скорость и угловое ускорение твердого тела в переносном и относительном движениях
3.1. Понятия переносной угловой скорости и переносного углового ускорения в сложном движении твердого тела
Дадим понятия векторов мгновенной угловой скорости и мгновенного углового ускорения твердого тела в его переносном движении.
Определение 2
Переносной
мгновенной угловой скоростью 
и переносным мгновенным угловым
ускорением 
твердого
тела в его сложном движении называются
соответственно
вектор мгновенной угловой скорости и
вектор мгновенного углового ускорения
подвижной системы координат
относительно абсолютного пространства.
Сопоставляя
данное определение 2 с определением 4
из §2 для векторов
и
,
видим, что
и
.
Как
и вектор
,
вектор
связан с движением базиса
,
,
системы
в абсолютном пространстве в любой момент
времени
соотношением (4.2.5)
§2:
. (4.3.2)
В (4.3.2)
вектор-функции
,
,
задаются
своими проекциями на оси абсолютной
системы координат,
которые совпадают в каждый момент
с элементами матрицы
,
соответственно:
проекции вектор-функции
совпадают с элементами
первого
столбца,
— второго,
— третьего
столбца.
Поэтому можем записать
(4.3.3)
Разложения
векторов
по базису
получаются дифференцированием по
времени
соотношений (4.3.3):
(4.3.4)
Из
них следует, что координаты векторов
в абсолютной системе в момент времени
совпадают с элементами соответствующих
столбцов матрицы
:
координаты
— с первым столбцом,
— со вторым,
— с третьим столбцом.
Вектор
определяется либо дифференцированием
вектора
,
т.е.
,
либо по формуле
. (4.3.5)
В
ней разложение векторов
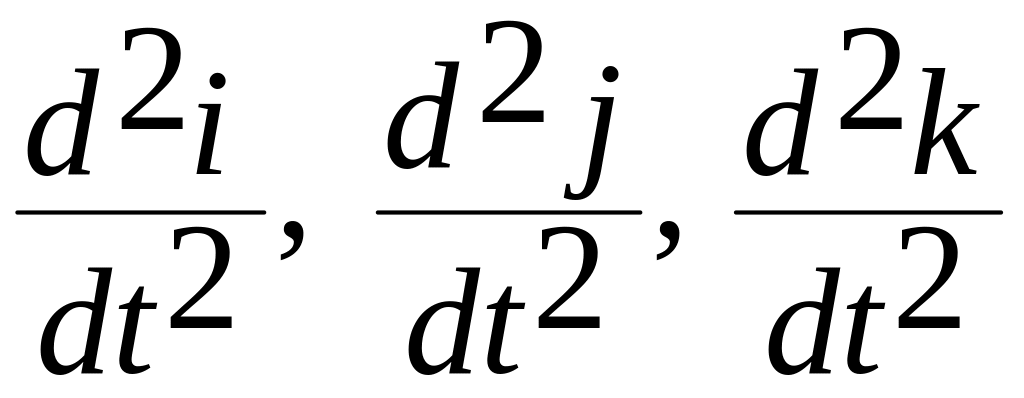по базису
в любой момент времени
получается дифференцированием по
соотношений (4.3.4).
Таким образом, будем иметь
(4.3.6)
3.2. Понятия относительной угловой скорости и относительного углового ускорения в сложном движении твердого тела
Дадим понятия векторов мгновенной угловой скорости и мгновенного углового ускорения твердого тела в его относительном движении.
Определение 3
Вектором
мгновенной угловой скорости 
и вектором мгновенного углового
ускорения 
относительного движения твердого тела
называются, соответственно, вектор
мгновенной угловой скорости и вектор
мгновенного углового ускорения твердого
тела при его движении относительно
подвижной системы координат
,
условно принимаемой неподвижной.
Из данного определения следует, что
, (4.3.7)
. (4.3.8)
Здесь
и
означают условные производные первого
и второго порядка от вектор-функций 
,
заданных своими проекциями на оси
подвижной системы
через элементы матрицы
ориентации твердого тела в подвижном
пространстве. При таком дифференцировании
базис
системы
условно принимается неподвижным.
Легко заметить, что выражения (4.3.7) и (4.3.8) для векторов и получаются из формул (4.3.2) и (4.3.5)
, (4.3.2)
, (4.3.5)
путем замены в правых частях равенств (4.3.2) и (4.3.5):
подвижного базиса переносного движения на базис связанной системы координат ;
дифференцирования
в абсолютной системе на условное
дифференцирование
.
Поскольку
векторы 
в проекциях на базис
«условно неподвижной» системы координат
в момент времени
задаются элементами соответствующих
столбцов матрицы
перехода от связанной системы к системе
,
то можем записать
,
, (4.3.9)
.
В (4.3.9) векторы , вообще говоря, зависят от времени . Однако в определении относительного движения твердого тела зависимость их от времени не учитывается. Иначе говоря, при описании движения твердого тела по отношению к системе отсчета полагается, что такое движение тело совершает в пространстве , условно принятом за абсолютное пространство.
Тем самым относительное движение тела определяется относительным движением полюса его связанной системы и движением базиса этой системы относительно базиса , условно принятого неподвижным.
Разложения
векторов
по базису
получаются дифференцированием по
времени
соотношений (4.3.9),
причем дифференцируются только
направляющие косинусы
,
,
а базис
не дифференцируется:
(4.3.10)
Аналогичным дифференцированием соотношений (4.3.10) строятся разложения векторов
