§10. Распределение ускорений в твердом теле (формула Ривальса)

10.1. Вывод формулы Ривальса

Выведем формулу для вычисления ускорения любой точки твердого тела. По определению ускорения любой точки  можем записать

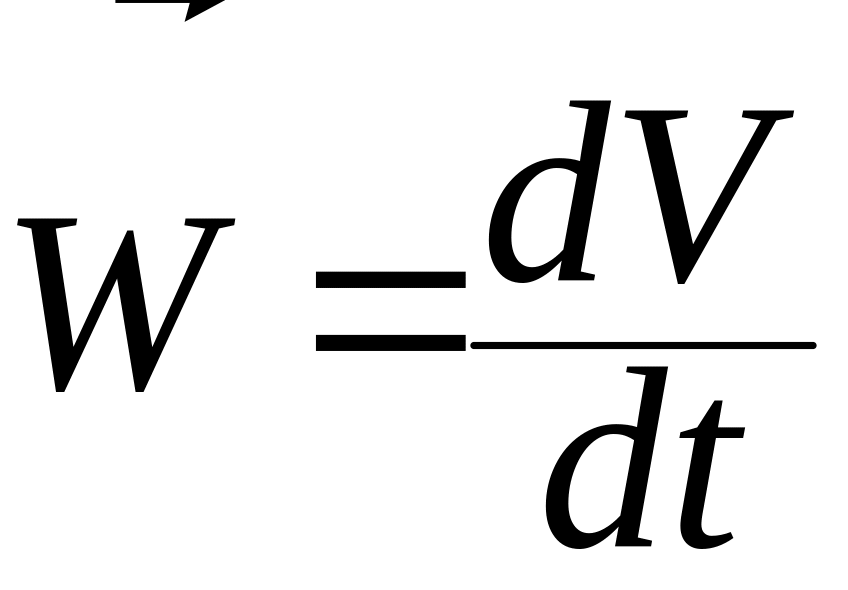, (3.10.1)

где — скорость точки , а — ее ускорение.

Согласно формуле Эйлера скорости точек твердого тела определяются следующей зависимостью от векторов  , и :

, (3.10.2)

где

— скорость полюса связанной системы координат,

— положение полюса связанной системы координат относительно неподвижной точки отсчета,

— вектор мгновенной угловой скорости твердого тела,

— положение точки твердого тела в связанной системе координат,

, (3.10.3)

— координаты точки  в связанной системе (постоянные величины),

— базис связанной системы координат.

Подставляя (3.10.2)

, (3.10.2)

в (3.10.1)

, (3.10.1)

и дифференцируя по  , получим

. (3.10.4)

Очевидно, 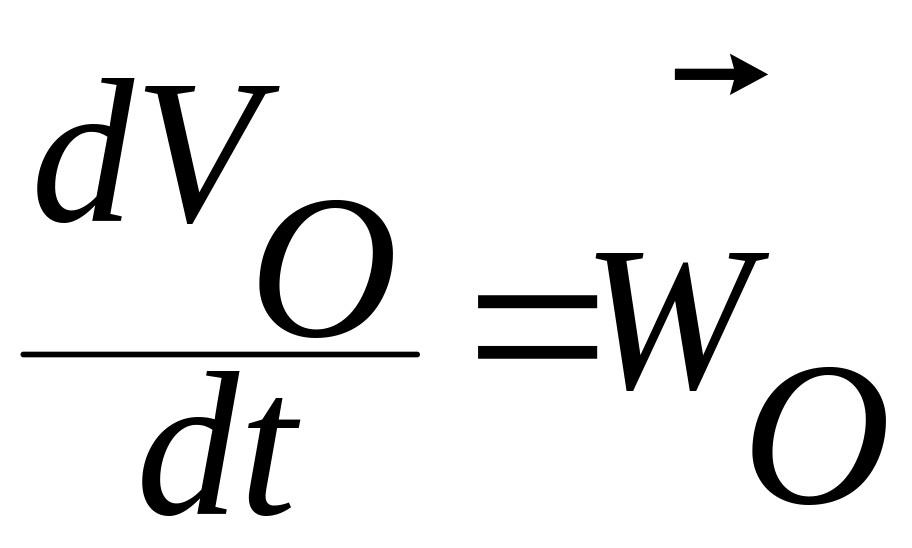— это ускорение полюса связанной системы координат (по определению).

Поскольку вектор неподвижен в связанной системе координат, то согласно лемме 3 (из п.3 §8) имеем

. (3.10.5)

Введем обозначение:

. (3.10.6)

Определение

Вектор , задаваемый формулой (3.10.6), где — вектор мгновенной угловой скорости твердого тела, называется вектором мгновенного углового ускорения твердого тела.

Подставляя (3.10.5) и (3.10.6) в правую часть соотношения (3.10.4) и заменяя в нем первое слагаемое на  , приходим к следующему выражению для ускорения :

. (3.10.7)

Оно называется формулой Ривальса.

Формулу Ривальса (3.10.7) запишем в виде

.

В ней каждое слагаемое имеет свое название. А именно,

— ускорение полюса связанной системы координат;

— вращательное ускорение точки твердого тела при ее вращении вокруг полюса связанной системы координат;

— осестремительное ускорение точки твердого тела.

10.2. Кинематические характеристики твердого тела

Формула Ривальса позволяет вычислить ускорение любой точки  твердого тела по ее положению в теле и кинематическим характеристикам этого тела, заданным в любой момент времени  .

Кинематическими характеристиками твердого тела называются вектора  , , , , и матрица  , где

— положение полюса связанной системы координат;

— скорость полюса связанной системы координат;

— ускорение полюса связанной системы координат;

— вектор мгновенной угловой скорости твердого тела;

— вектор мгновенного углового ускорения твердого тела;

— матрица ориентации твердого тела.

Знание этих векторов и матрицы ориентации позволяет вычислить положение, скорость и ускорение любой точки твердого тела, если заданы ее координаты в связанной системе координат.

10.3. Связь координат вектора углового ускорения и вектора угловой скорости

Пусть вектор задается своими проекциями на связанные оси

. (3.10.8)

Установим связь проекций на связанные оси вектора мгновенного углового ускорения твердого тела с проекциями  вектора мгновенной угловой скорости на эти оси.

Теорема

Справедливо следующее равенство

. (3.10.9)

Доказательство

Дифференцируя обе части равенства (3.10.8) по и учитывая формулы Эйлера (3.8.14) из §8

,

получим

.

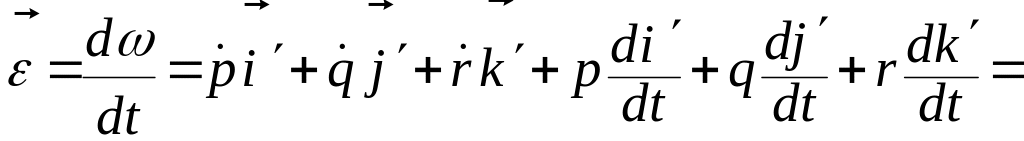
Поскольку , то приходим к (3.10.9). Теорема доказана.

Формула (3.10.9)

. (3.10.9)

показывает, что проекции вектора углового ускорения твердого тела на связанные оси совпадают с производными от соответствующих проекций на эти оси вектора угловой скорости.