3º. Следствия из формулы Эйлера

Пусть , где и — две любые, несовпадающие точки твердого тела (см. рис. 3.9.1).

Обозначим и скорости точки и точки  , соответственно.

Рис. 3.9.1

Следствие 1

В любой момент времени  справедливо равенство:

, т.е. .

Иначе говоря, в любой момент времени  совпадают проекции скоростей двух точек твердого тела на ориентированную прямую, соединяющую эти две точки.

Доказательство

Возьмем в качестве полюса связанной системы точку . Тогда в любой момент  согласно формуле Эйлера будем иметь

.

Умножая скалярно на орт , получим

.

Что и требовалось доказать.

Следствие 2

Если скорости и двух точек и твердого тела коллинеарны в момент времени  , причем в том случае, когда они сонаправлены — величины этих скоростей не равны между собой, то и в этот момент ортогональны прямой, соединяющей точки и (см. рис. 3.9.2).

Доказательство

Пусть в момент времени  , где — любое вещественное число, кроме .

Тогда для этого момента  по формуле Эйлера можем записать

.

Подставим . Получим

.

Рис. 3.9.2

Поскольку , то отсюда следует, что ортогонален , а тогда (поскольку коллинеарен ) и вектор будет ортогонален .

Что и требовалось доказать.

Следствие 3

В произвольный момент времени  скорость любой точки твердого тела однозначно может быть вычислена по известным в этот момент скоростям и положениям трех его точек, не лежащих на одной прямой.

Доказательство

Пусть в момент времени  для трех точек твердого тела, не лежащих на одной прямой, известны скорости и положения  , соответственно.

Обозначим , . Тогда , . Поскольку не лежат на одной прямой, то и — неколлинеарные векторы. Введем вектор и аффинную систему координат с полюсом в точке и базисом .

В этой системе можем записать

. (3.9.4)

Согласно формуле Эйлера имеем

, .

Подставляя в правые части этих равенств вектор из (3.9.4), придем к системе двух векторных уравнений относительно неизвестных :

,

.

Умножим каждое из уравнений скалярно на и найдем :

, .

Умножим первое уравнение скалярно на . В результате найдем :

.

Подставим в соотношение (3.9.4) для угловой скорости . Получим:

. (3.9.5)

Тогда согласно формуле Эйлера для любой точки твердого тела скорость будет определяться по следующей формуле:

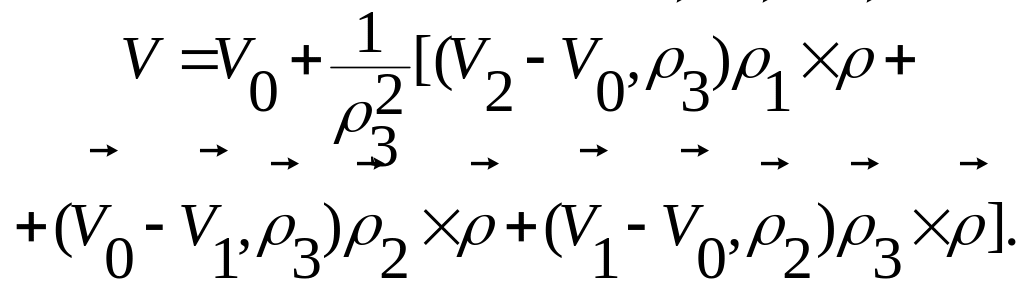(3.9.6)

где . Что и требовалось доказать.

Следствие 4

Если в момент времени  , то скорости всех точек одинаковы. Иначе говоря, в состоянии мгновенного покоя и мгновенного поступательного движения скорости всех точек одинаковы.

Доказательство

Действительно, если в момент времени  , то согласно формуле Эйлера

.

Здесь — скорость любой точки  твердого тела. Из формулы следует, что она совпадает с — скоростью полюса связанной системы координат.

Согласно принятой классификации движений, при тело либо находится в мгновенном покое (тогда ), либо совершает мгновенное поступательное движение (тогда ).

Этим доказано утверждение следствия 4.

Следствие 5

Если в момент времени  скорости трех точек твердого тела, не лежащих на одной прямой, равны по величине и направлению, то тело совершает мгновенное поступательное движение или находится в мгновенном покое.

Доказательство

Из равенства (3.9.5) в момент  вытекает, что при выполнении условий следствия. Поэтому, если , то тело находится в мгновенном покое. Если , то тело совершает мгновенное поступательное движение (согласно принятой классификации движений). Следствие 5 доказано.

Объединяя следствия 4 и 5, можем сделать вывод:

твердое тело, содержащее хотя бы три точки, не лежащие на одной прямой, находится в мгновенном покое или совершает мгновенное поступательное движение тогда и только тогда, когда в момент времени  указанные три его точки имеют одинаковые скорости.

Следствие 6

Если в момент времени  скорости двух точек и твердого тела равны нулю, то:

1. все точки прямой, проходящей через них, имеют скорость, равную нулю;

2. вектор мгновенной угловой скорости твердого тела коллинеарен этой прямой или равен нулю;

3. тело совершает мгновенное вращение вокруг неподвижной оси или находится в мгновенном покое.

Доказательство

Пусть для точек   и  твердого тела в некоторый момент времени  имеем и , где — скорость точки  , — скорость точки  .

1). Покажем сначала, что в момент времени вектор  будет коллинеарен прямой, проходящей через точки   и  .

Действительно, согласно формуле Эйлера имеем

.

Отсюда следует равенство

.

Из него находим

, (3.9.7)

т.е. вектор в момент  коллинеарен указанной прямой.

2). Покажем, что если точка  твердого тела находится на прямой, проходящей через точки и , то ее скорость будет равна нулю.

Ранее было доказано, что если точка  находится на данной прямой в некоторый момент времени  , то и при всех  она будет находиться на ней при любых движениях твердого тела.

Поэтому в любой момент времени  . Здесь

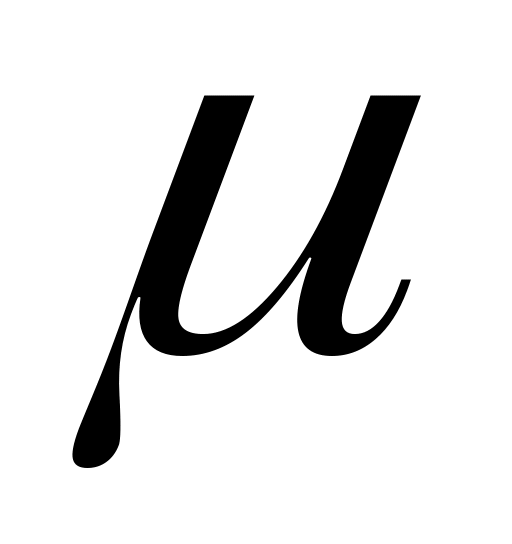• — постоянная величина,

;

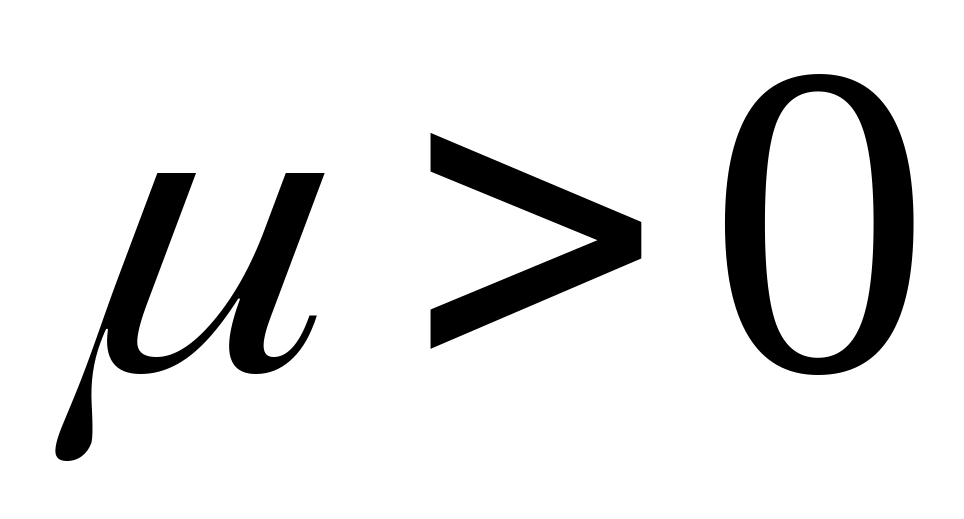• , если точки и находятся по одну сторону от точки ;

• , если точки и находятся по разные стороны от точки .

По формуле Эйлера находим скорость  точки  в момент  :

.

Поскольку в этот момент вектор  коллинеарен , а вектор  коллинеарен  , то и векторы и коллинеарны. А потому и, следовательно, .

Таким образом, доказали, что все точки твердого тела, находящиеся на прямой, проходящей через точки   и  , будут иметь в момент времени  скорости, равные нулю.

3). Покажем теперь справедливость утверждения 3) следствия.

Действительно, если в момент  в (3.9.7)

, (3.9.7)

имеем , то тело будет находиться в мгновенном покое, поскольку и в указанный момент.

Если в момент  , то тело совершает мгновенное вращение вокруг оси , ибо , а точки   и  имеют скорости, равные нулю.

При этом все точки твердого тела, принадлежащие оси  , также имеют скорости, равные нулю. Следствие 6 доказано.