31

ЛЕКЦИЯ 12. КИНЕМАТИКА. Глава 3. (Лекция 3 по главе 3) §8к С.1-16. §9 С.16-28. §10 С.28-33. 31.07.2012

Глава 3. Кинематика твердого тела

§8. Мгновенная угловая скорость твердого тела

2º. Понятие вектора мгновенной угловой скорости подвижной системы координат

Будем рассматривать подвижную систему координат с базисом и полюсом  . Пусть — положение полюса  относительно абсолютной точки отсчета .

Чтобы задать движение подвижной системы координат, надо задать движение  полюса  и задать в любой момент времени положение ортов .

2.1. Задание движения подвижного базиса и его кинематических характеристик

Положение ортов в любой момент времени можно определить одним из двух способов:

• либо через известные векторные функции ;

• либо через известную матрицу ориентации  .

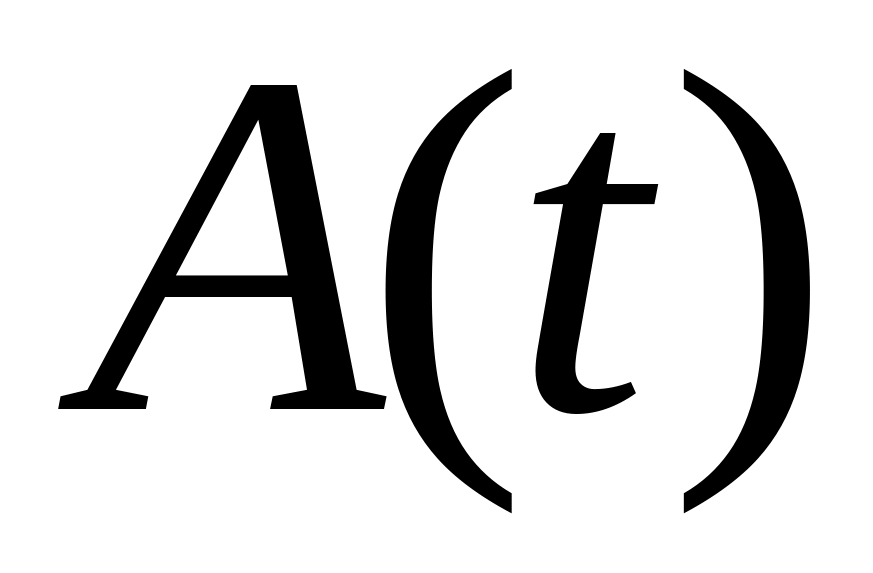Векторные функции ,  будем считать дважды непрерывно дифференцируемыми по времени .

Пусть положение ортов определяется через функции :

, , .

Тогда в каждый момент времени известны скорости изменения направления этих ортов.

Поскольку функции образуют правую ортонормированную тройку векторов в любой момент времени  , то для них справедливы следующие тождества по времени :

(3.8.7)

Дифференцируя соотношения (3.8.7), придем к следующим тождествам, связывающим функции и их производные :

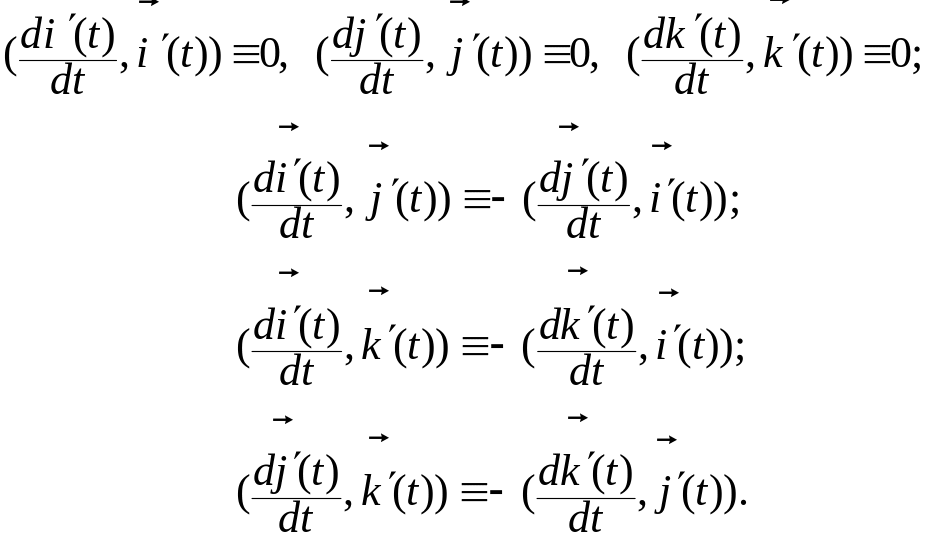(3.8.8)

Пусть теперь положение ортов задается через матрицу  перехода к абсолютной системе .

Обозначим через орты абсолютной системы, а через ,  , — элементы матрицы перехода  . Тогда, исходя из определения матрицы перехода, можем записать

(3.8.9)

Дифференцируя по каждое из этих равенств, получим

(3.8.10)

Таким образом, векторы 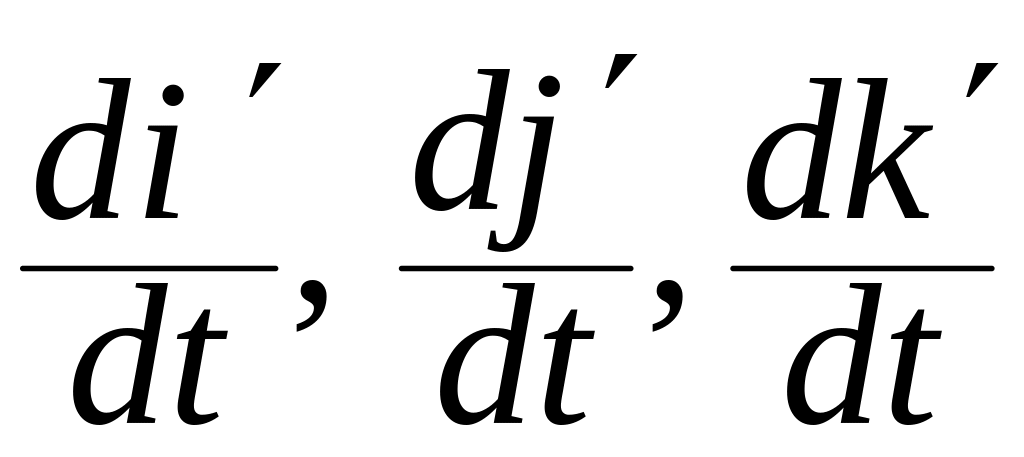вычисляются по формулам (3.8.10) через элементы матрицы  . Поскольку матрица  задана, то элементы матрицы  можно считать известными.

Тем самым в любой момент времени известны векторы .

Заметим, что матрицу можно считать заданной и в том случае, когда задаются функции , ибо столбцы матрицы  совпадают с координатами векторов в абсолютной системе координат.

Таким образом, из проведенных рассуждений можно сделать следующие выводы.

1. При любом способе задания движения подвижной системы координат в любой момент времени будут известны векторы

, , . (3.8.11)

2. Эти векторы получаются непосредственным дифференцированием функций , если положение ортов в каждый момент времени  задается через указанные функции .

В случае, когда положение ортов в каждый момент времени задается через матрицу ориентации , векторы вычисляются по формулам (3.8.10)

(3.8.10)

3. При всех значениях времени будут выполняться тождества (3.8.7) и (3.8.8):

(3.8.7)

(3.8.8)

2.2. Вектор угловой скорости и углового ускорения подвижной системы координат

Обратимся теперь к уравнениям (3.8.1). Обозначим в них

. (3.8.12)

Тогда в любой момент времени для векторов  , , справедливы соотношения (3.8.2):

, , , , . (3.8.2)

Кроме того, для векторов , , задаваемых формулами (3.8.11)

, , , (3.8.11)

в совокупности с векторами , , справедливы условия (3.8.3), (3.8.4).

, ; (3.8.3)

, , . (3.8.4)

Указанные свойства проверяются подстановкой (3.8.11) и (3.8.12) в формулы (3.8.7) и (3.8.8).

А потому справедлива теорема 1, доказанная выше (п.1º), т.е.

существует единственный вектор , задаваемый формулой

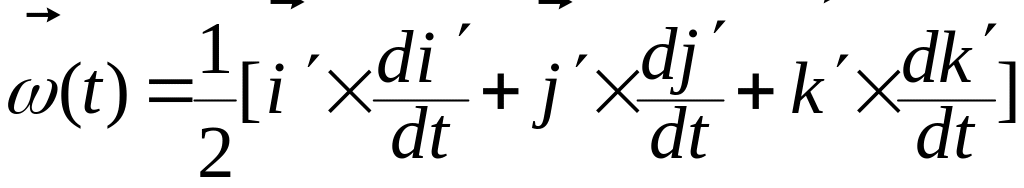, (3.8.13)

который в любой момент времени является решением следующей системы векторных уравнений

. (3.8.14)

Определение 1

Вектор , вычисляемый по формуле (3.8.13):

, (3.8.13)

называется вектором мгновенной угловой скорости подвижной системы координат.

Из теоремы 1 следует, что он является единственным решением уравнений (3.8.14)

. (3.8.14)

Уравнения (3.8.14) называются уравнениями Эйлера.

Они устанавливают связь мгновенной угловой скорости с базисными вектор - функциями и их производными по времени  .

Поскольку — дважды непрерывно дифференцируемые векторные функции, то из формулы (3.8.13) следует, что вектор , рассматриваемый как функция времени , также непрерывно дифференцируемая векторная функция.

Это свойство вектора позволяет ввести следующее понятие.

Определение 2

Вектор , задаваемый формулой

,

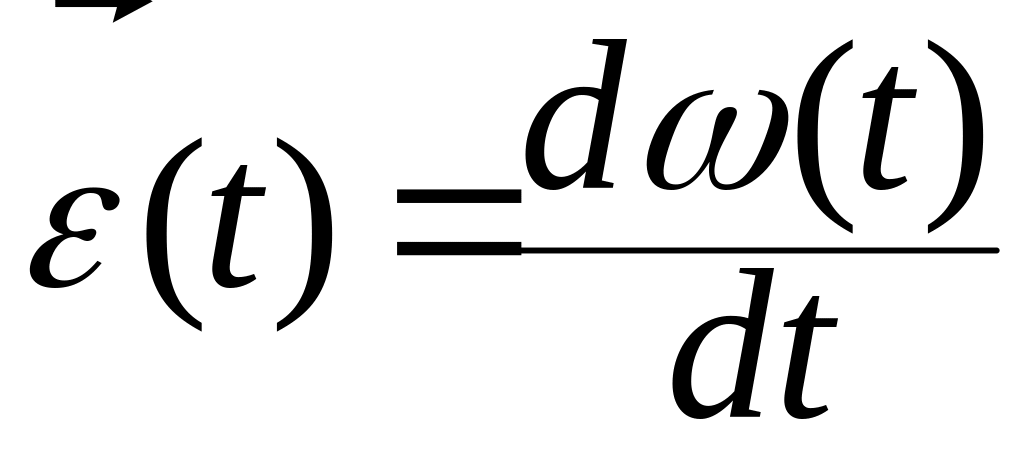называется вектором мгновенного углового ускорения подвижной системы координат. Здесь — вектор мгновенной угловой скорости подвижной системы координат.

Из определения 2 и формулы (3.8.13) для вектора  легко выводится формула связи мгновенного углового ускорения  с базисными вектор-функциями  и их вторыми производными по времени  :

.

Вычислим проекции вектора на подвижные оси . Для этого последовательно умножим скалярно на равенство (3.8.13). При умножении на орт получим:

.

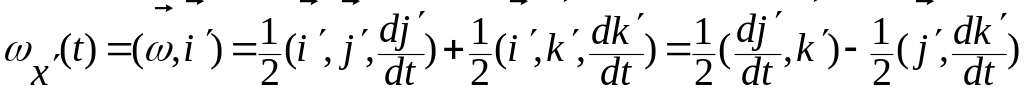Здесь учли, что

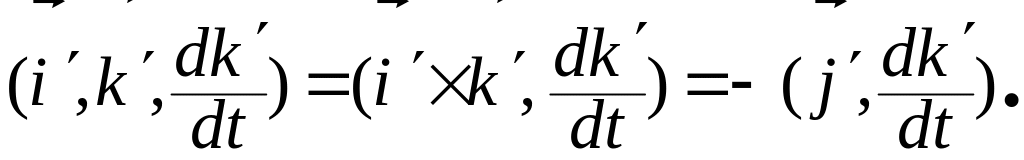
Из тождеств (3.8.8)

(3.8.8)

имеем:

.

Поэтому окончательно находим

. (3.8.15)

Выражения для проекций , получим из формулы (3.8.15) круговой перестановкой

, .

Будем иметь

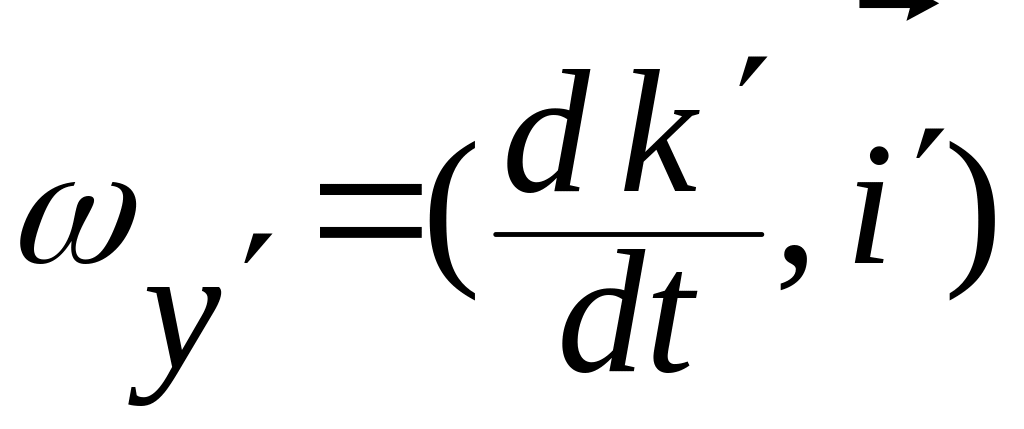, . (3.8.16)

Справедливость их легко проверить умножением равенства (3.8.13)

, (3.8.13)

на векторы и скалярно.

Если в соотношения (3.8.15), (3.8.16) подставить (3.8.9) и (3.8.10):

(3.8.9)

(3.8.10)

являющиеся выражениями векторов , через элементы матрицы и ее производной , то получим связь проекций вектора на подвижные оси с направляющими косинусами векторов и их производными.

Эта связь имеет вид:

(3.8.17)

Формулы (3.8.17) позволяют вычислить вектор в проекциях на связанные оси через элементы матрицы ориентации и их производные , .