4.3. Математические модели дифференциальных связей, задающих ограничения на обобщенные скорости

Покажем, что ограничения на обобщенные скорости  , которые накладывают кинематические связи в неголономных системах, можно записать

в форме уравнений дифференциальных связей, зависящих от ,  и .

Для этого в уравнения (2.6.21)

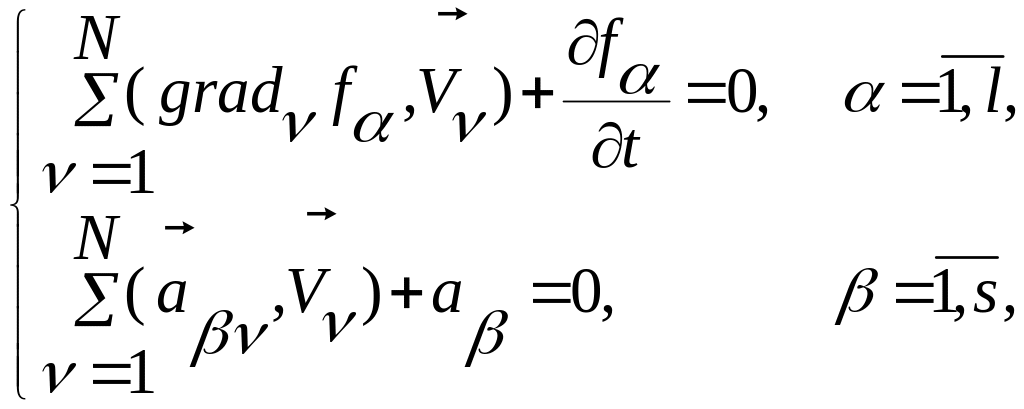(2.6.21)

подставим вместо скоростей , , их зависимости от обобщенных скоростей  , задаваемые формулами (2.6.3)

, , (2.6.3)

а вместо векторов ,  — их зависимости (2.6.1) от и

, . (2.6.1)

Проделав указанные подстановки, будем иметь:

, , (2.6.23)

, . (2.6.24)

Группа уравнений (2.6.23) совпадает с системой (2.6.18)

, . (2.6.18)

Как было показано, левые части (2.6.18) при любых значениях  , и принимают нулевые значения.

Следовательно, (2.6.23) является системой тождеств относительно  ,  и .

Поэтому ограничения на обобщенные скорости будут задаваться только уравнениями (2.6.24), которые после очевидных преобразований приводятся к следующему виду:

, . (2.6.25)

В (2.6.25) введены обозначения

, .

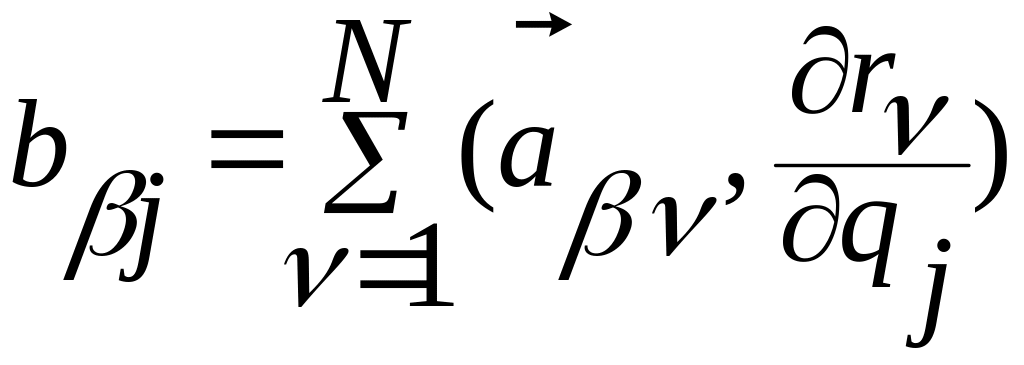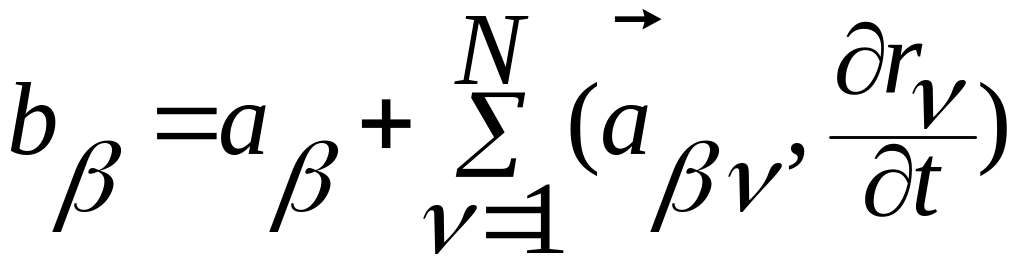Запишем теперь в матричной форме вторую группу уравнений (2.6.21) и уравнений (2.6.25), задающих ограничения на скорости  , , и на обобщенные скорости  .

Матричная запись второй группы уравнений (2.6.21)

, , (2.6.21)

примет вид

. (2.6.26)

Соответственно, система (2.6.25)

, , (2.6.25)

запишется в форме

. (2.6.27)

В (2.6.26) матрица  определяется формулой (2.5.4) из §5:

. (2.5.4)

В ней введены обозначения:

, , ,

— координаты вектора  в заданной системе отсчета.

Вектор-столбец в (2.6.26)

(2.6.26)

составлен из свободных членов ,  , левых частей второй группы уравнений (2.6.21)

, . (2.6.21)

В уравнениях (2.6.27)

(2.6.27)

вектор-столбец составлен из свободных членов ,  , в левых частях системы (2.6.25)

, . (2.6.25)

Матрица  имеет размерность  . Она связана с матрицами   и  следующей зависимостью

. (2.6.28)

Таким образом, подводя итог проведенному анализу неголономных связей с целью построения ограничений, накладываемых ими на обобщенные скорости, можем сделать следующее заключение.

Вывод 3

1. Ограничения на обобщенные скорости неголономной системы определяются системой линейных уравнений (2.6.25)

, , (2.6.25)

или в матричной форме — системой (2.6.27)

. (2.6.27)

В ней матрица коэффициентов  связана с матрицей  исходной системы кинематических связей соотношением (2.6.28)

. (2.6.28)

2. Среди обобщенных скоростей  , независимыми являются  обобщенных скоростей, а остальных зависят от них.

На этом завершаем изложение кинематики системы материальных точек.

В заключение дадим здесь несколько понятий, связанных с переменными  и , .

Пространство переменных  называется координатным пространством, или иначе, пространством конфигураций, а значения переменных  называются координатами точки в пространстве конфигураций.

Точка пространства конфигураций, координаты которой совпадают со значениями обобщенных координат механической системы в момент времени  , называется изображающей точкой.

Обобщенные координаты  , обобщенные скорости  и время  , рассматриваемые как независимые переменные, называются переменными Лагранжа.

В соответствии с этими определениями уравнения (2.6.27)

. (2.6.27)

являются уравнениями линейных дифференциальных связей в пространстве конфигураций.

Легко доказать, что эти уравнения будут неинтегрируемыми. Поэтому связи (2.6.27), математическими моделями которых они являются, называются неголономными связями в пространстве конфигураций.