4º. Ограничения на обобщенные координаты и обобщенные скорости, накладываемые связями в неголономных системах

4.1. Отсутствие ограничений на обобщенные координаты в неголономных системах

В неголономных системах, так же, как и в голономных, выбор обобщенных координат  для описания движений механической системы производится на основе уравнений голономных связей (2.6.15)

, . (2.6.15)

Эти уравнения входят в состав математических моделей связей в неголономных системах, задаваемых кинематическим способом.

Неинтегрируемые дифференциальные связи, обязательно присутствующие в описании неголономной системы, на выбор переменных  и на область их допустимых значений не влияют.

Тем самым они не накладывают никаких ограничений на обобщенные координаты.

Выше (в п.3º) показано, что геометрические связи (2.6.15) также не накладывают ограничений на эти координаты.

Следовательно, вывод 1, полученный для голономных систем, будет справедлив и для систем неголономных.

4.2. Ограничения на обобщенные скорости в неголономных системах

Обратимся теперь к решению вопроса, какими уравнениями описываются ограничения на обобщенные скорости, создаваемые связями в неголономных системах.

Ранее было показано (см. §5, п.1º), что связи, действующие в таких системах, накладывают ограничения на скорости , . Они задаются уравнениями

(2.6.21)

Матрица коэффициентов при скоростях в системе (2.6.21) совпадает с матрицей, определяемой по формуле (2.5.3) из §5:

,

где обозначает матрицу вида (2.4.3) из §4, а — матрицу вида (2.5.4) из §5.

(2.4.3) из §4,

(2.5.4) из §5.

Ранг матрицы  удовлетворяет условию (2.5.5) из §5:

.

Как отмечалось в п.2º из §5, это условие позволяет утверждать, что

компонент скоростей  , , можно выразить из уравнений (2.6.21)

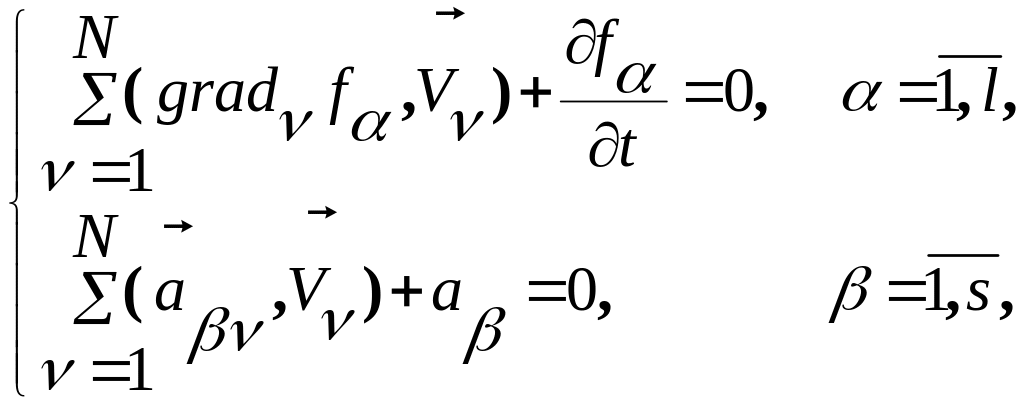(2.6.21)

как функции остальных оставшихся компонент.

Поэтому можно записать:

, (2.6.22)

где

— вектор-столбец, составленный из компонент скоростей точек системы,

— вектор-функция размерности .

Величины  обозначают те компонент вектора скорости механической системы , через которые выразили из уравнений (2.6.21) остальных компонент.

Подставляя зависимости (2.6.22) в равенство (2.6.10), связывающее и вектор

, (2.6.10)

находим:

.

Отсюда делаем вывод, что:

независимыми являются не все обобщенные скорости , а только из них.

Данное заключение вытекает из того, что обобщенных скоростей зависят от независимых компонент .

Таким образом, относительно неголономных систем справедливы следующие утверждения.

1. Связи, действующие в неголономных системах, накладывают ограничения на обобщенные скорости.

2. Из этих ограничений обобщенные скорости могут быть выражены как функции от m независимых переменных , являющихся координатами векторов скоростей точек механической системы.