1.1. Зависимость скоростей и ускорений от обобщенных скоростей и обобщенных ускорений
Согласно
определению обобщенных координат любое
положение 
связано с обобщенными координатами
,
,
соотношениями
,
. (2.6.1)
Тогда
на движении
имеем
. (2.6.2)
Дифференцируя
(2.6.2) дважды по
,
получим прямые зависимости
и
,
,
от
,
,
и
,
,
соответственно:
,
, (2.6.3)
(2.6.4)
Проведем анализ этих соотношений.
Равенства (2.6.3) можем записать в матричном виде:
, (2.6.5)
где
— матрица Якоби размерности 
системы (2.6.1), составленная по переменным
,
а
— векторы-столбцы размерности
,
,
,
соответственно.
Поэлементно они представляются так:
,
,
,
,
,
,
,
,
,
,
.
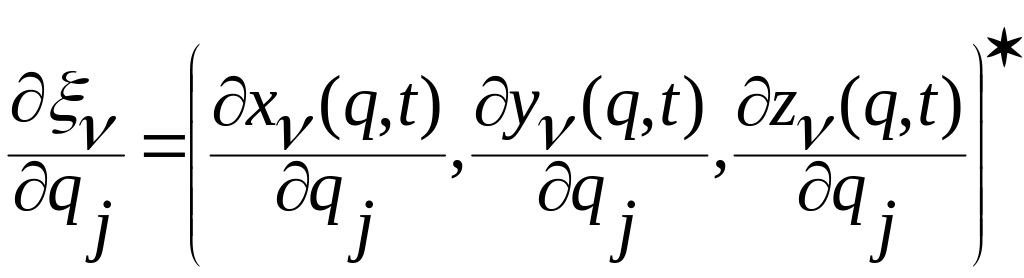Звездочки
обозначают операцию транспонирования.
Согласно определению обобщенных координат неголономной механической системы и условию 3, которое накладывается на соотношения (2.6.1)
, (2.6.1)
в определении 4 обобщенных координат голономной системы (см. п.3º, §4), имеем
. (2.6.6)
Прежде чем продолжить анализ соотношений (2.6.1) – (2.6.5), докажем следующее утверждение.
1.2. Лемма о линейной независимости столбцов матрицы
Пусть
дана любая прямоугольная матрица
размерности
,
.
Лемма
Для того чтобы столбцы матрицы были линейно независимы, необходимо и достаточно, чтобы матрица
была
неособой, т.е.
.
Доказательство
Очевидно,
матрица 
является квадратной размерности
.
Необходимость
Пусть
столбцы матрицы
линейно независимы. Тогда для любого
вектора 
размерности
выполняется
. (2.6.7)
Предположим,
что
— особая матрица. Тогда существует
вектор
такой, что
,
или, подставляя
,
получаем
. (2.6.8)
Поскольку
,
то, умножая равенство (2.6.8) на
слева, получаем
.
Этот
результат противоречит условию (2.6.7),
так как (2.6.7) выполняется для любого
вектора
(в частности, оно справедливо и для
).
Значит, предположение о том, что
,
неверно. Необходимость доказана.
Достаточность
Пусть . Предположим противное, что столбцы матрицы линейно зависимы. Тогда существует вектор размерности такой, что
. (2.6.9)
После
умножения равенства (2.6.9) на
слева, получим
.
Отсюда следует, что вектор является решением однородной системы уравнений.
Матрица
коэффициентов этой системы совпадает
с матрицей
,
которая имеет
.
А это означает, что такая система может
иметь только нулевое решение
.
Пришли к противоречию с условием . Лемма доказана.
1.3. Зависимость обобщенных скоростей и обобщенных ускорений от скоростей и ускорений точек механической системы
Вернемся к равенствам (2.6.5)
. (2.6.5)
Они справедливы на любых движениях и любых положениях механической системы.
Умножая равенства (2.6.5) на слева, получаем
.
Учитывая условие (2.6.6)
(2.6.6)
и
утверждение леммы
(из условия (2.6.6) следует, что столбцы
матрицы
линейно независимы; из леммы следует
тогда, что матрица
неособая при любых
),
находим
. (2.6.10)
Если
в матрице
и в векторе 
аргумент
заменить обратной функцией
,
получаемой из соотношений (2.6.1),
то формула (2.6.10)
даст однозначную зависимость обобщенных
скоростей 
от скоростей
на любом положении
механической системы в любой момент
времени
.
Поэтому из (2.6.10) можно сделать вывод:
обобщенные скорости на любых движениях и в любых положениях однозначно связаны со скоростями механической системы.
Объединяя теперь равенства (2.6.5) и (2.6.10)
, (2.6.5)
, (2.6.10)
приходим
к следующему заключению относительно
связи между скоростью 
и обобщенными скоростями механической
системы:
между скоростью и обобщенными скоростями механической системы в любых ее положениях существует взаимно однозначное соответствие, определяемое формулами (2.6.5) и (2.6.10).
Аналогичным путем из (2.6.4)
(2.6.4)
получаем
(2.6.11)
где
и
обозначают векторы-столбцы размерности
,
составленные из компонент
ускорений
и компонент
вектор-функций
,
,
соответственно.
Функции
строятся по функциям 
,
которые имеют вид
(2.6.12)
Чтобы
получить 
,
необходимо в (2.6.12)
заменить аргументы
на
,
а обобщенные скорости
— на их зависимость от
,
найденную по формулам (2.6.10).
Обобщая сказанное, можем утверждать, что соотношения (2.6.1), (2.6.3), (2.6.4)
, , (2.6.1)
, , (2.6.3)
(2.6.4)
дают прямые зависимости положений, скоростей и ускорений от обобщенных координат, обобщенных скоростей и обобщенных ускорений.
На них можно смотреть как аналитические зависимости положений, скоростей и ускорений механической системы, однозначно разрешимые относительно обобщенных координат, обобщенных скоростей и обобщенных ускорений.
Обратная зависимость обобщенных скоростей и обобщенных ускорений от скорости и ускорения механической системы задается соотношениями (2.6.10) и (2.6.11), соответственно:
, (2.6.10)
(2.6.11)