30) Теоретические основы современных информационных сетей. Информационные ресурсы сетей.

Рассматриваются два характерных типа сетей: с коммутацией пакетов и коммутацией каналов. В первом случае, через сеть от источника к получателю по некоторому маршруту, выбор которого определяется проектом сети, передаются пакеты, т.е. блоки данных переменной длины. В случае коммутации каналов, для пары пользователей устанавливается маршрут передачи от одного конца к другому.

Такие параметры, как число и длина пакетов, поступающих в сеть или проходящих через неё в любой момент времени, число вызовов, поступающих на вход сети за заданное время, продолжительность занятия (ресурса) – в общем случае подвержены статистическим изменениям. Поэтому для изучения их воздействия на сеть и получения соответствующих количественных характеристик должны применяться вероятностные методы.

Ключевую роль в анализе сетей играет теория очередей (называемая также теорией массового обслуживания)

Для сетей с коммутацией пакетов проблема очередей возникает совершенно естественно. Пакеты, поступающие на вход сети или промежуточного узла, на пути к пункту назначения накапливаются, обрабатываются с целью выбора подходящего канала передачи к следующему узлу, а затем считываются в этот канал, когда наступит время их передачи. Время, затраченное на ожидание передачи в накопителе, является важной мерой, характеризующей работу сети. Оно зависит от времени обработки в узле и длины пакета, а также от пропускной способности канала передачи и дисциплины обслуживания, применяемой при обработке пакета.

Теория очередей возникает также при исследовании сетей с коммутацией каналов. Во-первых, при изучении обработки вызовов, во-вторых, при анализе зависимости между числом доступных каналов и вероятностью того, что вызов, требующий установление соединения, будет заблокирован или поставлен в очередь для ожидания обслуживания.

Рассмотрим простейшую модель обслуживания:

накопитель

В качестве пакетов будем рассматривать пакеты данных для случая коммутации пакетов или вызовы для систем с коммутацией каналов.

Пакты поступают случайным образом со скоростью  в единицу времени. Они ожидают обслуживания в накопителе, и обслуживаются в соответствии с некоторой конкретной дисциплиной со средней скоростью  пакетов в единицу времени. На рисунке показана одна обслуживающая линия. В более же общем случае могут быть доступны несколько обслуживающих линий, и в этом случае одновременно могут обслуживаться несколько пакетов. В контексте сети передачи данных обслуживающая линия  это средство передачи (исходящий канал или линия, передающие пакеты или, в случае систем с коммутацией каналов, обрабатывающие вызовы), которое передает данные с предписанной скоростью C блоков данных в единицу времени. Таким образом, процесс обслуживания определяется длиной пакета или продолжительностью соединения.

Если интенсивность поступления  приближается к скорости обработки пакетов , очередь начинает расти. При накопителе конечной ёмкости очередь достигает наибольшей допустимой величины, а при переполнении накопителя поступление всех последующих пакетов будет заблокировано.

Для однолинейных систем обслуживания стабильность обеспечивается при . Введём параметр . Его называют коэффициентом использования канала или интенсивностью нагрузки. Когда  приближается к 1 или превышает её, возникает область перегрузки, и поступающие пакеты блокируются более часто.

Характеристики сети (время задержки, вероятность блокировки и т.д.) зависит также от вероятности состояний очереди. Для расчёта вероятностей состояния должны быть известны следующие характеристики:

• процесс поступления пакетов (статистика входящих потоков);

• распределение длин пакетов (распределение времени обслуживания);

• дисциплина обслуживания (обслуживание в порядке поступления – ОПП или FIFO, некоторые дисциплины обслуживания с приоритетами).

Для многолинейных систем вероятности состояний зависят также от числа обслуживающих линий.

В теории массового обслуживания принято моделировать процесс поступления вызовов с помощью Пуассоновского процесса.

Пуассоновский процесс

Рассмотрим бесконечно малый промежуток времени t (t0), проходящий между моментами t и t+t. При определении пуассоновского процесса используются три основные предпосылки:

1. вероятность одного поступления в течение времени t определяется в виде: t+О(t), где О(t) – члены более высокого порядка, которыми мы можем пренебречь при t0;

1. вероятность нулевого поступления в течение времени t равна 1-t;

2. поступление – без последействия (без памяти), т.е. поступление в течение t не зависит от предыдущих поступлений.

Если теперь рассмотреть большой промежуток времени Т, то вероятность p(k) того, что в промежутке Т произойдут k поступлений, равна:

, где k = 0, 1, 2, …

Это равенство называется распределением Пуассона. Оно нормировано:

и его среднее значение имеет вид:

.

Дисперсия распределения:

.

Теперь рассмотрим большой промежуток времени и отметим на нём моменты, в которые наступили события Пуассоновского процесса.

Очевидно, что  - это положительная случайная величина с непрерывным распределением. Оказывается, что для Пуассоновского распределения величина  распределена по показательному закону:

Среднее значение показательного распределения:

а дисперсия .

Рассмотрим очередь из нескольких вызовов, ожидающих обслуживания. Отметим время завершения обслуживания:

Обозначим случайную величину, описывающую время между завершениями обслуживания через r. Эта же величина является временем обслуживания. Если r распределена по показательному закону со средним значением

E(r)=1/,

то плотность распределения будет равна:

.

Процесс обслуживания является полным аналогом процесса поступления и обладает всеми свойствами последнего. На основании этого вероятность завершения обслуживания в малом промежутке времени (t, t+t) в точности равна t + О(t), а вероятность незавершения обслуживания в промежутке (t, t+t) равна 1-t+О(t) независимо от предыдущих или последующих завершений.

Показательная модель обслуживания обладает свойством отсутствия последействия, которая используется как одна из определяющих предпосылок Пуассоновского процесса.

Ещё одно полезное свойство, объединяющее одну из причин, по которой Пуассоновский процесс часто используется для моделирования входящих потоков, заключается в том, что при объединении m независимых Пуассоновских потоков с произвольными интенсивностями ₁, ₂, … _m, объединённый поток также будет Пуассоновским с интенсивностью .

В применении к сетям такое положение возникает, когда статистически объединяются пакеты иди вызовы от ряда источников, каждый из которых генерирует их с Пуассоновской интенсивностью.

Система обслуживания М/М/1

Система обслуживания М/М/1 – это система с одной обслуживающей линией, Пуассоновским входящим потоком, показательным распределением обслуживания и дисциплиной ОПП (обслуживание в порядке поступления).

Диаграмма изменений состояний во времени для системы может быть изображена следующим образом:

Пусть процессы поступления и обслуживания определяются соответственно параметрами  и . Определим вероятность p_n(t+t) того, что в момент времени t+t в системе будет находиться n клиентов (пакетов или вызовов). Из диаграммы видно, что в момент времени t система могла находиться только в состоянии n-1, n или n+1. Тогда мы можем записать:

.

Вероятности перехода из одного состояния в другое получены в результате рассмотрения путей, по которым происходят эти переходы, и расчёта соответствующих вероятностей. Например, если система осталась в состоянии n, то могли произойти либо уход и одно поступление с вероятностью t, либо ни одного ухода или поступления с вероятностью 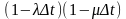, что и показано в первом случае.

Производя упрощения, иcпользуя разложение 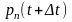в ряд Тейлора, можно получить следующее уравнение:

.

Для стационарного состояния вероятность p_n(t) приближается к некоторому постоянному значению, поэтому = 0. Тогда последнее уравнение для стационарного случайного процесса упрощается и принимает вид:

(1).

Форма уравнения (1) показывает, что при работе системы действует стационарный принцип равновесия: левая часть описывает интенсивность уходов из состояния n, а правая часть – интенсивность приходов в состояние n из n-1 или n+1. Чтобы существовали вероятности стационарного состояния, эти две интенсивности должны быть равны.

Рассмотрим диаграмму состояний для системы М/М/1

Ввиду предположений о Пуассоновском процессе поступления и уходов клиентов переходы имеют место только между соседними состояниями с показанными интенсивностями.

Уравнение (1) может быть решено несколькими способами. При простейшем их них может быть использовано условие равновесия. Если рассчитать общий «поток вероятности», пересекающий границу области 1, и приравнять исходящий поток к входящему, получиться уравнение (1). Область 2 охватывает всё множество точек от 0 до n. Поток, поступающий в эту область, равен p_n+1, а поток, покидающий её, равен p_n. Приравнивая эти два потока, получим: p_n+1=p_n. Повторяя последнее уравнение n раз, получим:

p_n=p_n-1; p₂=p₁;

…

p₃=p₂; p₁=p₀;

Следовательно,

Отсюда:

Значение р₀ для случая бесконечной очереди можно найти, используя нормирующее условие: . Просуммировав n вышеприведенных уравнений и учитывая нормировку, получим:

.

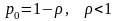Используя это, можно записать решение для установившегося режима:

. (2)

Распределение вероятностей (2) системы М/М/1 называется геометрическим распределением.

Обобщим результаты для случая конечной очереди, вмещающей не более N пакетов. Можно показать, то в этом случае:

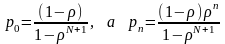
В частности, вероятность того, что очередь заполнена, совпадает с вероятностью блокировки:

.

На следующем рисунке приведён график вероятности блокировки в зависимости от нормированной нагрузки .

Область >1 называется областью перегрузки или скученности. Производительность системы, которая близка к нагрузке  при малых , выравнивается и при возрастании  приближается к пропускной способности .

Рассмотрим область <1. На основании определения среднего значения p_n, проведя суммирование, получим среднее число E(n) клиентов в системе, включая находящихся на обслуживании:

.

Это отражено на следующем рисунке:

При увеличении  среднее число клиентов в очереди резко возрастает за счёт (1-) в знаменателе.

Можно заметить, что при росте нагрузки системы растёт её производительность, однако при этом блокируется всё большее количество клиентов, а следовательно, растёт E(n), что ведёт к увеличению времени задержки в очереди.

Для нахождения времени задержки используют формулу Литтла:

E(T) = E(n), где E(T) – среднее время задержки в системе.

Для системы М/М/1, используя предыдущие формулы, можно получить: .

Информационные ресурсы сети Интернет

Обычно под словом «Интернет» понимается глобальная компьютерная сеть или «Сеть сетей». С точки зрения пользователя Интернет можно рассматривать как мощное глобальное средство обмена информацией. Одним из распространенных и перспективных серви-сов Интернет является сервис прямого доступа Word Wide Web — WWW, представляющий собой систему документов, включающих текстовую и графическую информацию, размещенных на узлах Интернет и связанных между собой гиперссылками.

Классификация источников информации в Интернете может проводиться по разным основаниям. По способам представления информации могут быть выделены следующие виды:

web-страницы — наиболее распространенный и используемый из информационных ресурсов. Этот ресурс представляет собой страницы гипертекста. Страницы наряду с текстовой могут содержать графическую, звуковую, видеоинформацию;

файловые серверы представляют собой реализацию в Интернете традиционного способа представления информации;

телеконференции могут являться важным источником информации. Они разбиваются на группы (рубрики) по тематике. Участвующие в телеконференциях могут написать свое сообщение или послать комментарии на чужое сообщение;

базы данных могут быть доступны через сеть Интернет. В них часто содержатся, кроме текстовой, также и другие виды информации.

Информационные ресурсы также могут быть разделены по языковому признаку. В сети Интернет представлены практически все основные языки, однако главным языком в силу исторически сложившихся традиций является английский. Ряд сайтов представляет информацию на нескольких языках.

В сети имеет место классификация и по территориальному признаку. Ряд сайтов предоставляет свою информацию для потребителей определенного региона, хотя доступ к сайту возможен и из любой точки сети.

Наиболее важным аспектом классификации информационных ресурсов сети Интернет является содержание информации. Деловая информация, необходимая в предпринимательской деятельности, по этому критерию может быть разделена на следующие группы.

1. Сведения о фирмах, организациях. Эта группа сведений существенно различается по своему наполнению для различных организаций. Различия определяются степенью освоения организацией возможностей Интернета по продвижению продукции или услуг. Различают три типа серверов данной группы (категории):

серверы присутствия в Интернете. Эти серверы могут быть разделены [11] на рекламные и информирующие серверы. Рекламный сервер обычно содержит одну или несколько страниц. Информирующий сервер содержит более подробную информацию о фирме и производимой ею продукции или оказываемых услугах;

информационные серверы. Целью этих серверов является предоставление различного рода информации потребителям. Серверы данной группы ведут информационно-аналитические агентства и другие структуры, в том числе государственные, чья деятельность связана с предоставлением различного рода информации потребителям;

интерактивные магазины. Серверы этой группы обеспечивают продажи товаров посредством Интернета. При этом могут быть реализованы в электронном виде следующие функции:

— предоставление клиенту необходимой информации о товаре или услуге;

— оформление заказа;.

— оплата заказа (при использовании онлайновых платежных систем);

— отправка полученного товара, если товаром является информация.

2. Сведения о состоянии мировой экономики и экономики отдельных стран. Данная информация представлена достаточно широко в профессиональных базах крупнейших информационно-аналитических агентств мира. Серверы этих агентств входят в состав информационных ресурсов сети Интернет. Однако сама инфор­мация, как правило, платная. Информация о состоянии национальной экономики обычно размещается на серверах государственных структур, отвечающих за государственную поддержку экономики, государственных статистических органов, различных экономических институтов.

3. Сведения о состоянии отраслевых рынков. Анализ отраслевых рынков осуществляют специализированные маркетинговые и консалтинговые агентства, а также маркетинговые службы фирм или организаций. Результаты этих исследований, используя Интернет, можно получить:

из профессиональных баз крупнейших мировых информационных агентств, найдя сведения о технологиях доступа к этим базам на сайтах Интернета;

в самих консалтинговых или маркетинговых агентствах, чьи сайты также представлены в Интернете;

в многопрофильных и отраслевых журналах, регулярно публикующих обзоры рынков. Одни издания, например многопрофильный журнал «Эксперт», представляют на сайтах оглавления номеров журналов. Другие, как, например, журнал «Профиль», размещают в открытом доступе публикуемые материалы.

4. Деловые новости. Подавляющее большинство мировых информационных агентств предоставляют потребителям доступ к профессиональным базам, содержащим деловые новости. Из зарубежных агентств крупнейшими поставщиками деловых новостей являются LEXIS-NEXIS, Dialog, Reuters. Среди отечественных агентств следует выделить:

«Интегрум-Техно», предоставляющий доступ к материалам 250 центральных и крупнейших региональных газет, а также к зарубежным новостям;

РИА «Новости» — государственное информационно-аналитическое агентство РФ;

«ИТАР-ТАСС» — государственное информационное телеграфное агентство РФ;

агентство «Интерфакс», входящее в состав международной информационной группы Interfax Information Services.

Интернет предоставляет бесплатный доступ к ежедневной электронной интернет-газете «Gazeta.ru». Ряд крупнейших газет имеют в Интернете электронные версии. Доступ к некоторым из них платный, например к электронным версиям печатных изданий Издательского дома «Коммерсантъ». К другим, например к элек­тронной версии газеты «Аргументы и факты», — бесплатный.

5. Справочная информация представлена в сети Интернет весьма широко. Это и списки web-сайтов компаний, отобранных по определенному принципу, и телефонно-адресный справочник «Желтые страницы» с возможностью поиска информации по названию фирмы и виду деятельности, и телефонные справочники городов Российской Федерации, стран СНГ и Балтии. Также в Интернете имеется информация о расписании движения поездов, авиарейсов, о погоде и многое другое.