Решение:

ЭДС самоиндукции, возникающая в контуре при изменении в нем силы тока I, определяется по формуле:  , где L – индуктивность контура. Знак минус в формуле находится в соответствии с правилом Ленца: индукционный ток направлен так, что противодействует изменению тока в цепи: замедляет его возрастание или убывание. Таким образом, ЭДС самоиндукции равна  . Абсолютная величина ЭДС самоиндукции равна 0,03 В. Индукционный ток направлен против часовой стрелки. При этом учтено направление тока в контуре и его возрастание со временем (что следует из заданного закона изменения силы тока).

Задание N 15.

Диэлектрическая проницаемость полярных газообразных диэлектриков зависит от …

Решение:

Диэлектрическая проницаемость  , где х – диэлектрическая восприимчивость, независящая от напряженности электрического поля и характеризующая свойства диэлектрика: дипольные моменты молекул и их концентрацию. Поскольку у полярных диэлектриков наблюдается ориентационная поляризация, диэлектрическая восприимчивость, а следовательно, и диэлектрическая проницаемость зависят от температуры.

Задание N 16.

Одно из уравнений Максвелла представляет собой обобщение закона полного тока для поля в веществе и математически может быть выражено уравнениями …

Решение:

Максвелл обобщил закон полного тока, предположив, что переменное электрическое поле наряду с токами проводимости является источником магнитного поля:

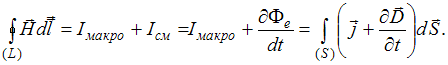
Вернуться к ответам.

Задание N 17.

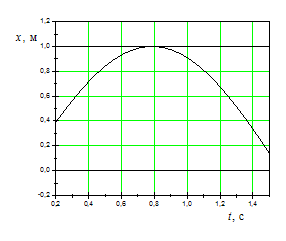
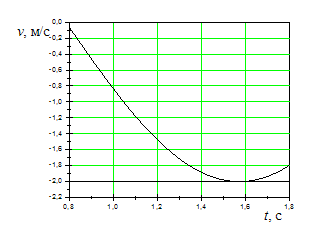
На рисунках изображены зависимости от времени координаты и скорости материальной точки, колеблющейся по гармоническому закону. Циклическая частота колебаний точки равна …

Решение:

Амплитудное значение скорости определяется по формуле  , где   амплитуда координаты (максимальное смещение материальной точки),   циклическая частота. Используя графики, находим   ,  (знак минус показывает, что точка в данный момент времени движется в отрицательном направлении оси  ). Следовательно,  .

Задание N 18.

Складываются два гармонических колебания одного направления с одинаковыми частотами и равными амплитудами  . Установите соответствие между разностью фаз складываемых колебаний и амплитудой результирующего колебания. 1.  2.  3.

Решение:

Амплитуда результирующего колебания, полученного при сложении двух гармонических колебаний одного направления с одинаковыми частотами, определяется по формуле  ,  где  и  – амплитуды,  ( ) – разность фаз складываемых колебаний. Если разность фаз   ,   , то   и   . Если  ,   , то   . Если   ,  , то  .

Задание N 19.

Поперечными волнами являются …

Решение:

В данной задаче упругими поперечными волнами являются волны, распространяющиеся вдоль струн музыкальных инструментов, так как в струне возникает деформация сдвига, и частички струны колеблются в направлении, перпендикулярном направлению распространения волны вдоль струны. Радиоволны и световые волны – электромагнитные, следовательно, также поперечные. В электромагнитной волне векторы напряженностей электрического и магнитного полей колеблются в плоскостях, перпендикулярных направлению распространения волны.

Вернуться к ответам.

Задание N 20.

Если в электромагнитной волне, распространяющейся в вакууме, значения напряженностей электрического и магнитного полей соответственно равны  , то объемная плотность энергии в микроджоулях на кубический метр составляет …