
Ответы тестирования по ФИЗИКЕ Задание N 1. |
Твердое
тело начинает вращаться вокруг оси
z. Зависимость углового ускорения |
Решение:
Угловое
ускорение характеризует быстроту
изменения угловой скорости тела ![]() .
При неизменной оси вращения векторы
.
При неизменной оси вращения векторы
![]() и
и ![]() совпадают
по направлению, если
совпадают
по направлению, если ![]() (угловая
скорость возрастает) и направлены
противоположно, если
(угловая
скорость возрастает) и направлены
противоположно, если ![]() (скорость
вращения уменьшается).
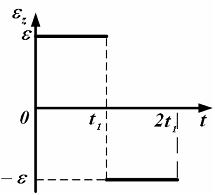
По условию
задания в интервале времени от 0
до
(скорость
вращения уменьшается).
По условию
задания в интервале времени от 0
до ![]() твердое
тело начинает вращаться вокруг оси
твердое
тело начинает вращаться вокруг оси ![]() с
постоянным угловым ускорением
с
постоянным угловым ускорением ![]() ,
следовательно, в этом интервале времени
угловая скорость
,
следовательно, в этом интервале времени
угловая скорость ![]() линейно
возрастает от 0 до значения
линейно
возрастает от 0 до значения ![]() (см.
рис.). В интервале времени от
до
(см.
рис.). В интервале времени от
до
![]() проекция
углового ускорения меняет знак,
проекция
углового ускорения меняет знак, ![]() ,
значит, угловая скорость в этом интервале
будет линейно убывать от значения
,
значит, угловая скорость в этом интервале
будет линейно убывать от значения ![]() до
0 (см. рис.).
до
0 (см. рис.).

Вернуться к ответам.
Задание N 2. |
|
Решение:
Согласно
второму закону Ньютона, ![]() .
В проекции на ось координат
.
В проекции на ось координат ![]() .
Следовательно,
.
Следовательно,  .
По геометрическому смыслу определенного
интеграла он равен площади под графиком
функции. Площадь под графиком функции
в интервале времени от 0 до 3 с равна
.
По геометрическому смыслу определенного
интеграла он равен площади под графиком
функции. Площадь под графиком функции
в интервале времени от 0 до 3 с равна ![]() ,
следовательно, импульс тела изменится
на
,
следовательно, импульс тела изменится
на ![]() .
.
Вернуться к ответам.
Тонкостенная
трубка и кольцо, имеющие одинаковые
массы и радиусы, вращаются с одинаковой
угловой скоростью. Отношение величины
момента импульса трубки к величине
момента импульса кольца равно …

Решение:
Величина
момента импульса тела, вращающегося
вокруг неподвижной оси, определяется
по формуле ![]() ,
где
,
где ![]() момент
инерции тела относительно заданной
оси,
момент
инерции тела относительно заданной
оси, ![]() угловая
скорость. Момент инерции тонкостенной
трубки равен
угловая
скорость. Момент инерции тонкостенной
трубки равен ![]() ;
момент инерции кольца, имеющего такую
же массу и радиус, равен моменту инерции
трубки, то есть
;
момент инерции кольца, имеющего такую
же массу и радиус, равен моменту инерции
трубки, то есть ![]() .
Отношение величин моментов импульсов
трубки и кольца равно:
.
Отношение величин моментов импульсов
трубки и кольца равно: 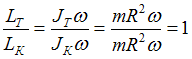 .
.
Вернуться к ответам.
Задание N 4. |
Кинетическая энергия тела (спутника), движущегося по круговой орбите вокруг Земли, меньше его гравитационной потенциальной энергии, взятой по модулю, в_____ раза. |
Уравнение
движения по круговой орбите вокруг
Земли:  .
Отсюда следует:
.
Отсюда следует:  .
Потенциальная энергия тела в гравитационном
поле Земли
.
Потенциальная энергия тела в гравитационном
поле Земли ![]() ,
т.е. кинетическая энергия в 2 раза меньше
гравитационной потенциальной энергии,
взятой по модулю.
,
т.е. кинетическая энергия в 2 раза меньше
гравитационной потенциальной энергии,
взятой по модулю.
Задание N 5. |
Экспериментатор,
стоящий на неподвижной скамье
Жуковского, получает от помощника
колесо, вращающееся вокруг вертикальной
оси с угловой скоростью |
Воспользуемся
законом сохранения момента импульса: ![]() .
Векторы момента импульса системы
.
Векторы момента импульса системы
![]() и
и ![]() до
поворота и после поворота оси вращения
колеса равны:
до
поворота и после поворота оси вращения
колеса равны: ![]() и
и
![]() ,
где
,
где ![]() и
и ![]() ,
, ![]() и
и ![]() –
моменты инерции и векторы угловых
скоростей человека со скамьей и колеса
соответственно. Следовательно,
–
моменты инерции и векторы угловых
скоростей человека со скамьей и колеса
соответственно. Следовательно, ![]() ,
а в проекциях на вертикальную ось:
,
а в проекциях на вертикальную ось: ![]() .
Знак минус показывает изменение
направления момента импульса колеса
при повороте его оси вращения на угол
.
Знак минус показывает изменение
направления момента импульса колеса
при повороте его оси вращения на угол ![]() .
Из последнего уравнения находим отношение
момента инерции тела человека вместе
со скамьей к моменту инерции колеса:
.
Из последнего уравнения находим отношение
момента инерции тела человека вместе
со скамьей к моменту инерции колеса:
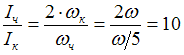
Задание N 6.
На
борту космического корабля нанесена
эмблема в виде геометрической
фигуры:
 Если
корабль движется в направлении, указанном
на рисунке стрелкой, со скоростью,
сравнимой со скоростью света, то в
неподвижной системе отсчета эмблема
примет форму, указанную на рисунке …
Если
корабль движется в направлении, указанном
на рисунке стрелкой, со скоростью,
сравнимой со скоростью света, то в
неподвижной системе отсчета эмблема
примет форму, указанную на рисунке …

 Соответствующая
зависимость угловой скорости
Соответствующая
зависимость угловой скорости  За
первые 3 секунды импульс тела изменится
на …
За
первые 3 секунды импульс тела изменится
на … 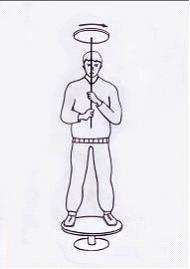
 Отношение
момента инерции экспериментатора со
скамьей к моменту инерции колеса равно
…
Отношение
момента инерции экспериментатора со
скамьей к моменту инерции колеса равно
…