Анализ систем

Пакет Control предоставляет широкий набор процедур, осуществляющих анализ САУ с самых различных точек зрения и, прежде всего, определение откликов системы на внешние воздействия, как во временной, так и в частотной областях.

Для нахождения временных откликов системы на внешние воздействия некоторых видов предусмотрены функции:

impulse – Нахождение отклика системы на импульсное входное воздействие;

step – Нахождение реакции системы на единичный скачок входного воздействия;

initial – Определение собственного движения системы при произвольных начальных условиях;

lsim – Определение реакции системы на заданное входное воздействие.

Воспользуемся данными процедурами для моделирования системы управления торпедой созданной в предыдущем разделе:

>> step(sys)

Используя эту команду можно получить ступенчатую переходную характеристику представленную на рис. 9. импульсную переходную характеристику (см. рис. 10) можно получить при помощи команды:

>> impulse(sys)

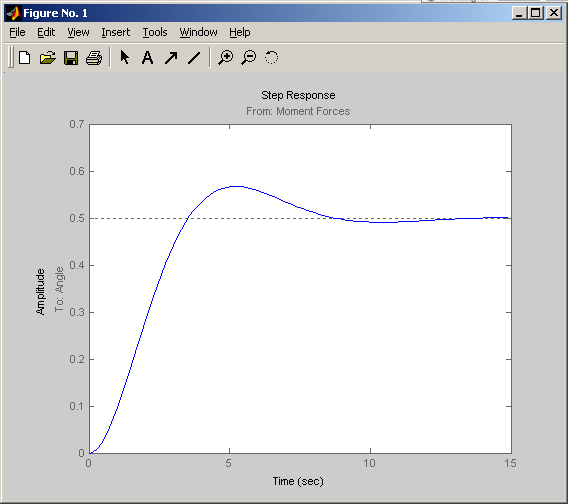
Рис. 9 Ступенчатая переходная характеристика

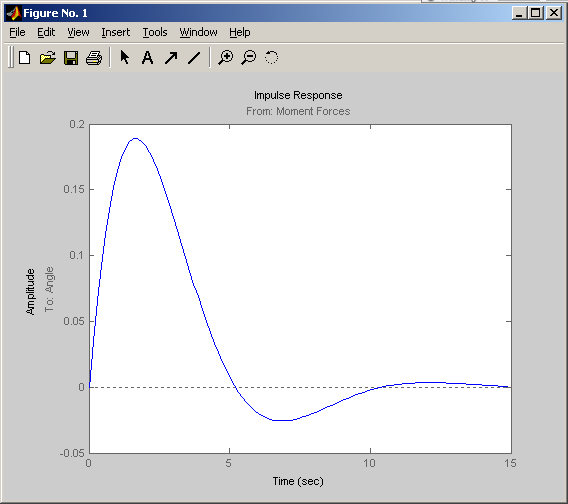
Рис.10 Импульсная переходная характеристика

Для моделирования системы при произвольном входном воздействии применяется процедура Lsim. Данная процедура применяется в виде Lsim(sys,u,t) где sys – имя модулируемой системы, u – вектор входного воздействия, t – вектор времени. Например моделирование ранее созданной системы управления торпедой при входном воздействии

где

шаг изменения времени равен 0,001 будет осуществляться при помощи следующего набора команд:

>> t=0:0.001:10;

>> u=sin(2*t.^2+t);

>> lsim(sys,u,t);

Результат моделирования показан на рис.11.

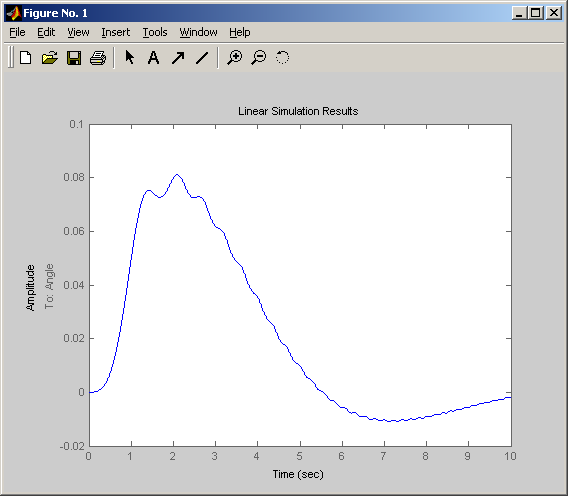
Рис. 11 Моделирование при произвольном входном воздействии

Для построения отклика в частотной области применяются следующие процедуры:

bode – Строит амплитудночатотную и фазочастотную характеристики (диаграмму Боде) указанной системы;

nyquist – строит в комплексной плоскости график амплитудно-фазовой характеристики (АФХ) системы в полярных координатах;

nichols – строит карту Николса системы, т. е. график АФХ разомкнутой системы в декартовых координатах;

sigma – строит графики зависимости частоты сингулярных значений системы; обычно совпадает с АЧХ системы.

Воспользуемся данными процедурами для исследования ранее созданной системы:

>> bode(sys)

>> nyquist(sys)

>> nichols(sys)

>> sigma(sys)

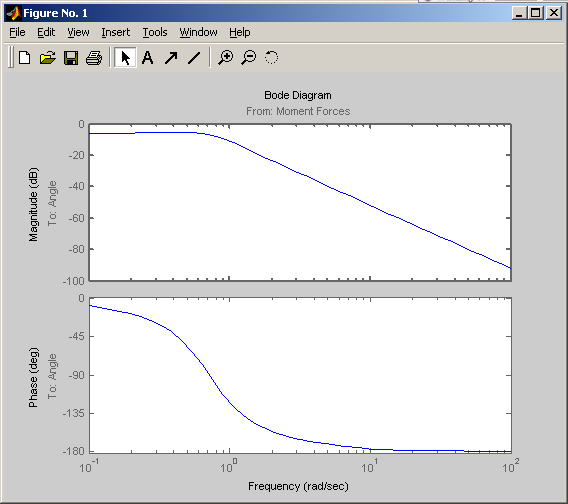
Рис. 12 Диаграмма Боде

Рис. 13 Диаграмма Найквиста

Рис. 14 Диаграмма Николса

Рис.15 График зависимости частоты сингулярных значений системы

Теперь рассмотрим процедуры, вычисляющие отдельные характеристики и графически показывающие расположение полюсов и нулей системы:

pole – расчет полюсов системы;

zpkdata – расчет полюсов, нулей и коэффициентов передачи системы;

gram – вычисление граммианнов системы;

pzmap – построение на комплексной плоскости нулей и полюсов системы;

damp – вычисление собственных значений системы;

rlocus – расчет и вывод в виде графиков и графическое окно траектории движения на комплексной плоскости корней полинома:

где - знаменатель передаточной функции; - числитель, при изменении положительного числа от 0 до бесконечности.

Для удобства использования средств control в состав пакта был включен специальный интерактивный обозреватель, который можно вызвать командой ltiview, окно которого представлено на рис 16. При помощи команды File Export можно экспортировать систему в обозреватель. При помощи команды Edit Plot Configuration можно выбирать характеристики для построения.

Рис. 16 Интерактивный обозреватель Ltiview