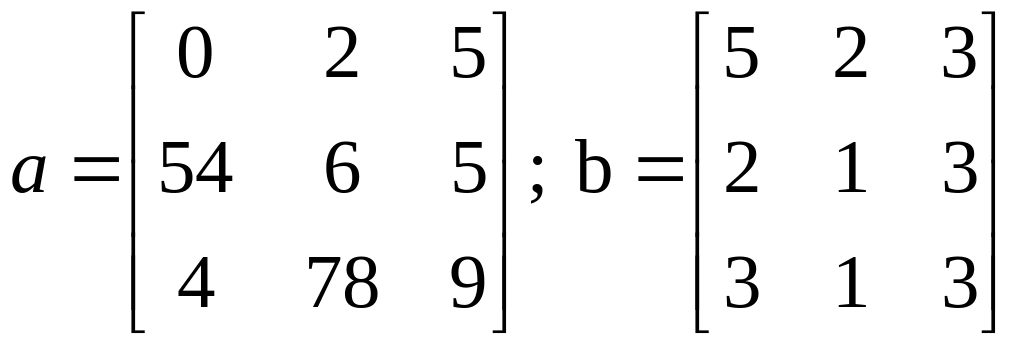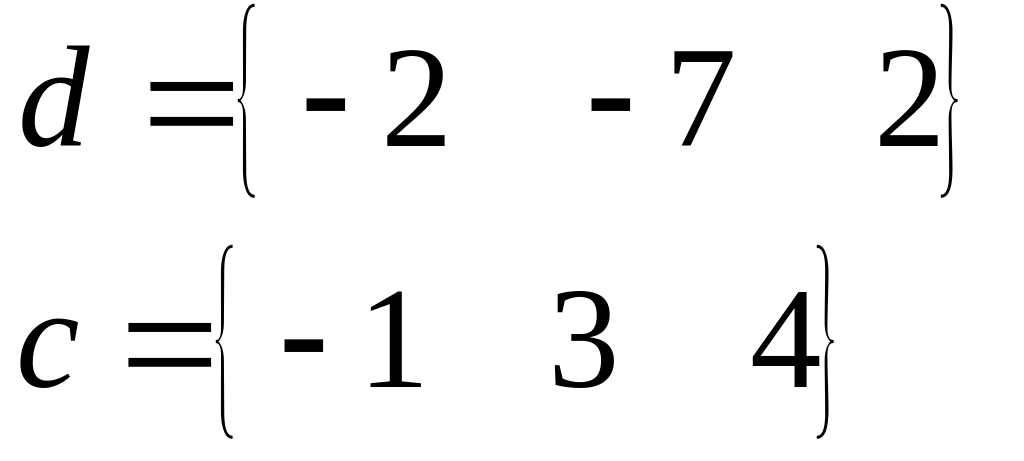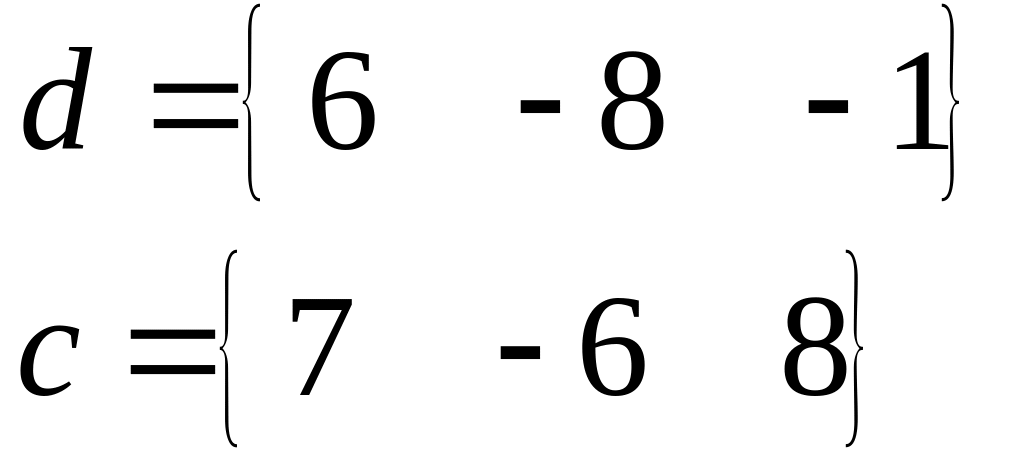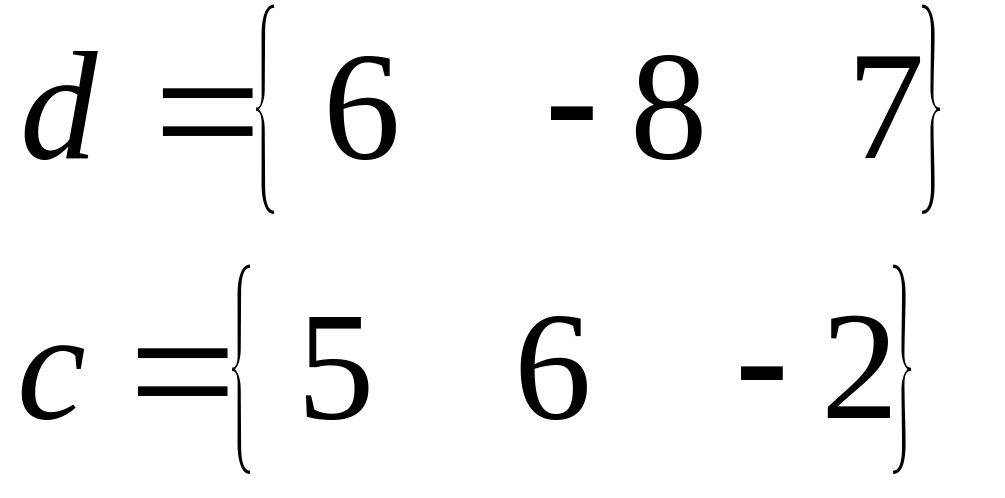Лабораторная работа №1 2
Основные операции и функции языка matlab 2
Лабораторная работа №2 17
Массивы и матрицы в языке Matlab. 17
Лабораторная работа №3 28
Средства графической визуализации matlab 28
Лабораторная работа №4 35
Программирование в matlab 35
Лабораторная работа № 5 43
Применение пакета matlab для исследования объектов управления. Использование пакета Control. 43
Лабораторная работа №1 Основные операции и функции языка matlab
Цель работы: Изучить основные операции и функции языка Matlab. Освоить программный интерфейс. Изучить принципы и приемы работы с системой математического моделирования matlab.
Рекомендации к выполнению лабораторной работы №1.
Система matlab является математической системой ориентированной на работу с матрицами, т.е. основным объектом системы matlab является прямоугольный числовой массив, который допускает комплексные переменные и ввод матриц без явного указания их размеров.
Выполнять вычисления в системе можно в двух основных режимах – режиме непосредственных вычислений и режиме программирования.
Для работы в режиме непосредственных вычислений используется командное окно matlab, которое появляется после запуска программы (см. рис. 1)
Командное окно служит для запуска встроенных программных модулей системы matlab, подачи команд операционной системе, вода и редактирования данных, подачи команд обработки данных, запуска приложений и произведения вычислений.
На командном окне расположены основные органы управления: строка меню 1, верхнее пиктографическое меню 2-6, 8-12. В командном окне отображается команда и результат ее выполнения, печать команды производится в командной строке 7, отмеченной символом >>.
рис. 1 Командное окно matlab.
Верхнее пиктографическое меню содержит следующие средства: 2 – создание нового файла, 3 – открытие документа, 4 – вырезать, 5 – копировать, 6 – вставить, 8 – отменить, 9 – вернуть, 10 – запуск системы simulink, 11, 12 – установка текущей директории.
Работа в режиме непосредственных вычислений производится при помощи набора команд в командной строке 7. Ввод чисел с клавиатуры производится по правилам, принятым для языков программирования высокого уровня:
Для отделения дробной части числа используется точка;
Десятичный порядок числа записывается в виде целого числа после символа е
Например:
>> 1.2035e -17
Символ ; используется для подавления вывода результатов вычисления. Нажатие клавиши Enter производит выполнение команды. В случае если строка получается длинной, используется символ переноса команды троеточие «…». Каждая введенная переменная по умолчанию считается прямоугольным числовым массивом, размер которого определяется в соответствии с введенными данными при этом, автоматически производится выделение памяти под него в связи, с чем отпадает необходимость в описании переменных.
Сохранение результатов. Работа с редактором отладчиком.
В ряде случаев появляется необходимость сохранения результатов работы. Система математического моделирования Matlab позволяет сохранять числовые данные, историю сессии (команды, введенные в командное окно) и текст программы. Для сохранения данных, полученных в результате работы, служит команда сохранения рабочего пространства. Под рабочим пространством понимаются все числовые данные, полученные в результате работы. Для сохранения рабочего пространства достаточно выбрать команду Save workspace as из меню File, при этом появляется окно сохранения файла, в котором необходимо указать размещение и имя файла содержащего данные из рабочего пространства. В ряде случаев возникает необходимость удалять лишние переменные и матрицы из рабочего пространства перед сохранением, для этого используется команда clear, после команды через пробел указывается имя переменной, например:
>>clear a;
в случае если имя переменной указано не было, происходит удаление всех переменных из рабочего пространства. Для просмотра списка переменных применяется команда whos. После удаления одной или нескольких матриц из рабочего пространства рекомендуется произвести дефрагментацию последнего, для чего служит команда pack, это уменьшает объем оперативной памяти занимаемый данными и увеличивает скорость вычислений. Также для работы с рабочим пространством можно использовать браузер вызываемый командой workspace (доступен только в версии 6.0 и выше), представленный на рис 6.
Рис 6. Браузер рабочего пространства.
Для сохранения сессии командного окна (под сессией понимается история введенных команд о результаты их выполнения) используется команда diary on (включить режим дневника), после этого в текущей директории создается текстовый файл, в который происходит запись сессии, для отключения режима дневника применяется команда diary off (режим дневника выключен).
В некоторых случаях
Для создания программ используется специальный редактор отладчик, окно которого представлено на рис 7., которое можно вызвать при помощи кнопки создания нового файла 2 см. рис. 1.
Рис 7. Окно редактора отладчика.
Основными средствами редактора отладчика являются: создание новой программы 1, открытие текста программы 2, сохранение программы 3, запуск программы 4, и закладки перехода от одного открытого окна к другому 5.
При составлении программ можно использовать все средства работы с командным окном. Результаты выполнения программы и сообщения об ошибках отображаются в командном окне.
Синтаксис языка: В качестве оператора присваивания используется символ =. В арифметических выражениях применяются следующие знаки:
+ сложение;
- вычитание;
* умножение;
/ деление;
^ возведение в степень;
\ деление в обратном порядке.
Основные математические функции языка:
sin(x) – синус;
asin(x) – арксинус;
cos(x) – косинус;
acos(x) – арккосинус;
tan(x) – тангенс;
atan(x) –арктангенс;
exp(x) – экспонента;
log(x) – натуральный логарифм;
log10(x) – десятичный логарифм;
abs(x) – модуль;
round(x) – округление;
floor(x) – выделение целой части числа;
rem(x) – остаток от деления.
sum(x) – сумма элементов вектора х.
Ввод формул производится аналогично языкам программирования высокого уровня.
Например: d=b^2-4*a*c.
Основные правила ввода матриц:
Матрица вводится в квадратных скобках;
Элементы строки отделяются друг от друга пробелами;
Строки отделяются друг от друга точкой с запятой.
Например:
>> a=[1 2 3; 4 5 6; 7 8 9]
a =
1 2 3
4 5 6
7 8 9
Основные действия с матрицами:
det(A) – вычисление определителя;
inv(A) – нахождение обратной матрицы;
A’ – транспонирование;
* – умножение матриц;
.* – поэлементное умножение матриц одинакового размера;
./ – поэлементное деление матриц одинакового размера;
+ – поэлементное сложение матриц одинакового размера;
- – поэлементное вычитание матриц одинакового размера;
\ – обратное умножение матриц, (причем от матрицы находящейся слева от знака вычисляется обратная матрица).
Например: Умножение матриц.
>> a=[1 2 3; 4 5 6; 7 8 9]
a =
1 2 3
4 5 6
7 8 9
>> b=[2; 5; 8]
b =
2
5
8
>> c=a*b
c =
36
81
126
Поэлементное умножение матриц и применение оператора .* приводит к следующему результату:
>> a=[1 2 3; 4 5 6; 7 8 9]
a =
1 2 3
4 5 6
7 8 9
>> a=[1 2 3]
a =
1 2 3
>> b=[2 5 8]
b =
2 5 8
>> c=a.*b
c =
2 10 24
следует отметить, что матричные операции поддерживают практически все функции Matlab.
Например:
>> a=[1 2 3; 4 5 6; 7 8 9]
a =
1 2 3
4 5 6
7 8 9
>> c=sin(a)
c =
0.8415 0.9093 0.1411
-0.7568 -0.9589 -0.2794
0.6570 0.9894 0.4121
в случае если в математическом выражении отсутствует оператор присваивания, то результат присваивается переменной ans.
Например:
>> 2/3
ans =
0.6667
Работа с векторами:
Посторенние таблицы значений функции
Пусть требуется построить таблицу значений функции
в точках 0.2, 0.3, 0.5, 0.8, 1.0, 1.2. Задача решается в два этапа:
Задается вектор значений аргумента х.
Вычисляются значения функции у.
>> x=[0.2 0.3 0.5 0.8 1.0 1.2]
x =
0.2000 0.3000 0.5000 0.8000 1.0000 1.2000
>> y=2.*x+(x.^2.*sin(x))./log(x)
Warning: Divide by zero.
y =
0.3951 0.5779 0.8271 -0.4575 Inf 9.7614
обратите внимание на применение знаков .* и ./, а также .^ в этом случае происходит поэлементное умножение, деление и возведение в степень элементов вектора. Данный пример также хорошо иллюстрирует особенности вычислений системы matlab: при значении аргумента равному единице возникает ошибка – в выражении знаменатель становится равным нулю. При этом matlab не останавливает вычислений, ограничиваясь предупреждением о делении на ноль (Warning: Divide by zero), результатом вычислений в этом случае будет inf, что означает равенство результата бесконечно большой величине.
В ряде случаев при математических вычислениях возникает необходимость задать алгебраический вектор в виде числовой последовательности с заданным шагом. Например, необходимо задать вектор значений аргумента х, при изменении х от 0 до 5 с шагом 0,2. Это достигается применением символа «:».
>> x=0:0.2:5;
причем на первое место ставится начальное значение, на второе шаг, на третье конечное значение. В этом случае желательно подавить вывод результата в командное окно, поставив в конце строки точку с запятой. В случае если шаг не указывается, то он принимается равным единице.
Задание на лабораторную работу №1
В соответствии с приведенными выше рекомендациями и вариантом задания необходимо при помощи системы Matlab произвести следующие вычисления:
Умножение и поэлементное умножение заданным матриц;
Транспонирование и нахождение обратной матрицы;
Вычислить скалярное и векторное произведение векторов.
Отчет по лабораторной работе должен содержать: введенные команды и полученные при этом результаты вычислений.
Варианты заданий:
Варианты матриц и находятся в таблице 1, а варианты функций и векторов в таблице 2.
Таблица 1
№ |
Матрицы |
1 |
|
2 |
|
3 |
|
4 |
|
5 |
|
6 |
|
7 |
|
8 |
|
9 |
|
10 |
|
11 |
|
12 |
|
13 |
|
14 |
|
15 |
|
16 |
|
17 |
|
18 |
|
19 |
|
20 |
|
21 |
|
22 |
|
23 |
|
24 |
|
25 |
|
26 |
|
27 |
|
28 |
|
29 |
|
30 |
|
Таблица 2
№ |
Функция |
Векторы |
1 |
|
|
2 |
|
|
3 |
|
|
4 |
|
|
5 |
|
|
6 |
|
|
7 |
|
|
8 |
|
|
9 |
|
|
10 |
|
|
11 |
|
|
12 |
|
|
13 |
|
|
14 |
|
|
15 |
|
|
16 |
|
|
17 |
|
|
18 |
|
|
19 |
|
|
20 |
|
|
21 |
|
|
22 |
|
|
23 |
|
|
24 |
|
|
25 |
|
|
26 |
|
|
27 |
|
|
28 |
|
|
29 |
|
|
30 |
|
|
