Модель процесса выбытия (дожития) старших возрастов у женщин.

Процесс моделирования дожития старших возрастов для женщин строится точно так же, как и процесс моделирования дожития старших возрастов для мужчин, только параметры двухпараметрического гамма-распределения, определяющего функцию дожития у женщин, другие, а именно

_w = 15 ,  _w = 0,34 sdvig _w = 24 .

Рабочая формула расчета f_w(x) с параметрами _w = 15,  _w = 0,34 примет вид:

f_w(x) = А_w ехр(_w lnx -  _w x) . (25)

Для функции fw(X) воспроизводятся все процедуры получения функций (13 – 16) w(z) w(z) с параметрами для когорты женщин и вычисляется функция w(z):

_w(z) = 0,5(_w(z) + _w(z)) . (26)

Функция _w(z), вычисленная таким образом, представляет собой коэффициент дожития для женщин. z  [25,100].

Для прогнозных целей параметры _w ,  _w , sdvig _w уточняются для каждого года прогноза. Функции дожития _w(z) и _m(z) представлены на рис. П3.3.

Теперь, когда известны модели и алгоритмы всех отдельных компонентов модели демографических процессов, рассмотрим целиком систему пошаговых прогнозных вычислений распределения по возрастным группам для когорты женщин.

Модель расчетов демографических процессов для когорты женщин.

Вычисления прогнозного распределения когорты женщин по возрастам производятся точно так же, как и для когорты мужчин, но с параметрами, соответствующими когорте женщин.

1. Вводится возрастная структура женского населения текущего года lMi(z) -«елочка»

2. Устанавливаются параметры прогнозных расчетов на заданное число лет и происходит запуск расчета.

В процессе расчета:

3. Производится передвижка возрастов - сдвиг «елочки» на один шаг, освобождая первый год и вытесняя последний:

LW_i+1(z) = LW_i(z+1) z  [1,100] . (27)

4. Первый элемент определяется через функцию рождаемости, коэффициент младенческой смертности и долю девочек, среди родившихся (5):

LW_i+1(1) = RW_i+1 . (28)

5. Добавляется миграция женской части населения, распределенная по возрастам:

LWM_i+1(z) = LW_i+1(z) + MW_i+1(z) . (29)

6. Учитывается смертность средних возрастов:

LWMM_i+1(z) = LWM_i+1(z) m_w(z) . (30)

7. Учитывается функция дожития. Значения «елочки» умножаются на коэффициент дожития для женщин: FLW_i+1(z) = LWMM_i+1(z) _w(z) . (31)

8. И новые значения «елочки» размещаются в новой обойме следующего прогнозного года: FLW_i+1(z)  LW_i(z) . (32)

9. Далее процесс (пункты 3-8) повторяется на заданное число лет прогноза.

Данные по общей численности населения, распределенной по возрастам, получаются суммированием прогнозных распределений мужчин и женщин:

LS_i+1(z) = LW_i+1(z) + LM_i+1(z) . (33)

Все этапы расчетов в системе моделей прогнозирования демографических показателей объединены в единый программно-технологический комплекс (ПТК).

Процессы миграции и смертности средних возрастов в настоящее время имеют компенсационный характер. Включение их в модель предусмотрено и является только предметом соглашения о сценарных параметрах этих процессов. В СМПДП и ПТК предусмотрена возможность управления параметрами расчетов для каждого года прогноза, а именно:

• параметрами рождаемости:

(4 параметра:  = 0,868;  = 0,466;  = 1,733; А = 0,042493);

• поправочным коэффициентом C, учитывающим родившихся младенцев в неизвестных возрастах матерей;

• параметрами дожития мужчин: (3 параметра: _m =10;  _m = 0,25; sdvig _m = 10);

• параметрами дожития женщин: (3 параметра: _w =15;  _w = 0,34; sdvig _w = 24);

• долей рождающихся девочек (0,4880,002);

• коэффициентом детской смертности (0,017).

Результаты прогнозных расчетов для когорт мужчин, женщин и всего населения на 2030 и 2060 годы представлены на рис. П3.4, П3.5, П3.6 соответственно.

Выводы:

1. Предложенные методы практически оказались достаточно простыми, очень гибкими, высокоточными, легко реализуемыми и легко настраиваемыми. Такие преимущества достигнуты за счет использования только аналитических функций.

2. Созданная система моделей прогноза демографических показателей (СМПДП) прозрачна и сценарно-управляема.

3. Разработанные инструментальные средства - программно-технологический комплекс (ПТК) - отличается простотой эксплуатации, высокой скоростью расчетов и достаточно развитыми средствами управления, настройки и визуального контроля сценарных и демографических процессов. (Время полного демографического прогнозного расчета одного варианта на 70 лет не превышает минуты).

Справочные сведения

Двухпараметрическое гамма-распределение. Плотность вероятности распределения случайной величина  для двухпараметрического гамма-распределения с параметрами  > -1,  > 0 имеет вид [51 с 121]

f(x) = x^v (34)

Сходимость функции распределения для (34) обеспечивается при всех  > -1, так как при х показательная функция e^x растет быстрее любой степенной функции и так как интеграл с нижним пределом 0 от x^a при а < 1 сходится.

Математическое ожидание и дисперсия : М = ( +1)/, D = ( +1)/².

Мода: x_mod = /,  0 . (35)

Коэффициент асимметрии: J1 = 2/(+1)^(1/2).

Коэффициент эксцесса: J2 = 6/(+1).

Установим связь параметров гамма-распределения с формой кривой распределения. Значение f(x) в точке x_mod равно

f_max(x_mod) = x^v_mod =

Автором установлено, что при фиксированных  и , ширина распределения x на уровне 0,5f_max(x_mod) выражается формулой:

х = x_mod = (36)

Из (35) и (36) имеем:

 = 2 x²_mod /x² (37)

 = 2 x_mod /x² (38)

С помощью этих соотношений можно в формуле (34) для гамма-распределения исключить  и  и ввести имеющие явный геометрический смысл параметры x_mod и x.

Гамма-распределение является непрерывным аналогом отрицательного биномиального распределения. При  = 0 гамма-распределение совпадает с показательным (экспоненциальным) распределением; при  = n/2-1,  = 1/2 с ² - (хи-квадрат) распределением с n степенями свободы. …При  = m и  = 1 гамма-распределение называют показательно-степенным распределением с параметром m.

Трехпараметрическое гамма-распределение. Плотность вероятности распределения случайной величина  для трехпараметрического гамма-распределения с параметрами  > -1,  > 0 и  имеет вид

f_r(x) = А_rx^v exp(-x^ ) (39)

Если интеграл f_r(x) x  (0, ) нормировать к 1, то А_r определяется формулой:

А_r = (40)

Мода x_mod = (/())'(1/),   0.

Частными случаями трехпараметрического гамма-распределения являются нормальное распределение, распределение Вейбулла-Гнеденко, ² - (хи-квадрат) распределение,  - (хи) - распределение [51 с.121-135]. При двух степенях свободы  - (хи) - распределение называется распределением Релея-Райса, при трех степенях свободы называется распределением Максвелла и др.

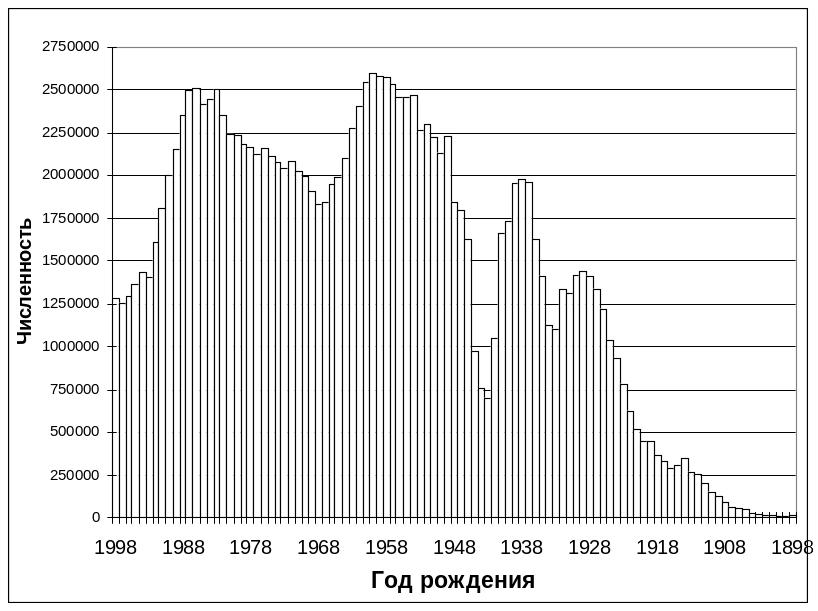
Рис. П3.1. Возрастная структура всего населения РФ на 1.01.1999 года.

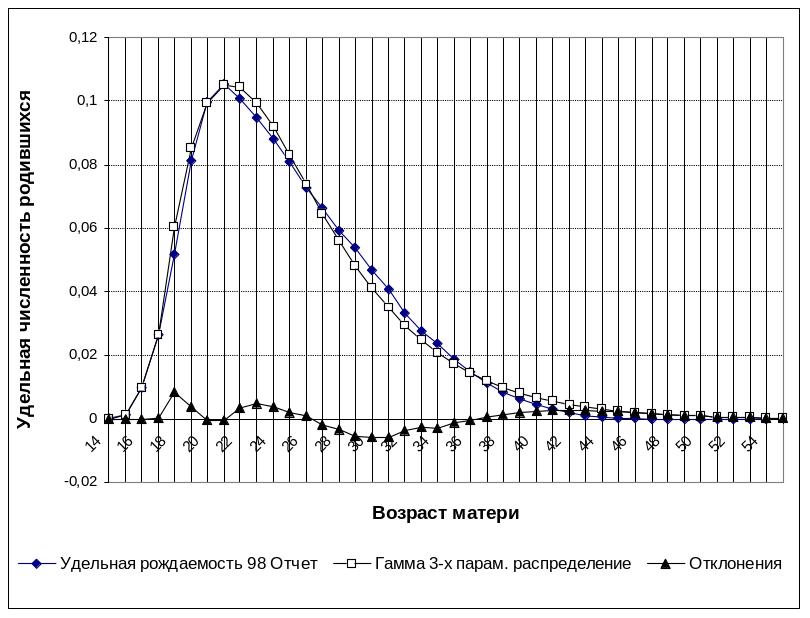
Рис. П3.2. Фактическая (отчет 1998 года) и теоретическая удельная рождаемость.

Рис. П3.3. Доли дожития старших возрастов (мужчин и женщин соответственно)

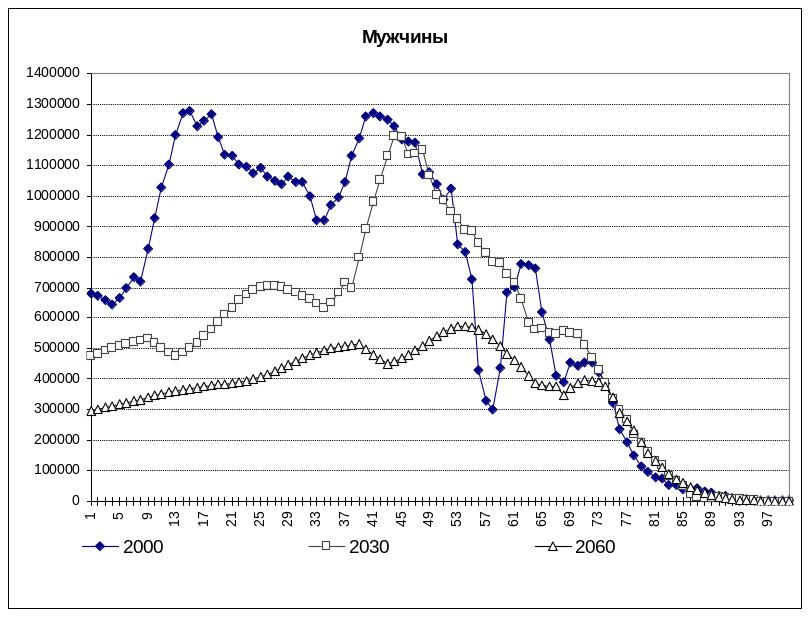
Рис. П3.4. Прогнозные распределения возрастной структуры мужчин.

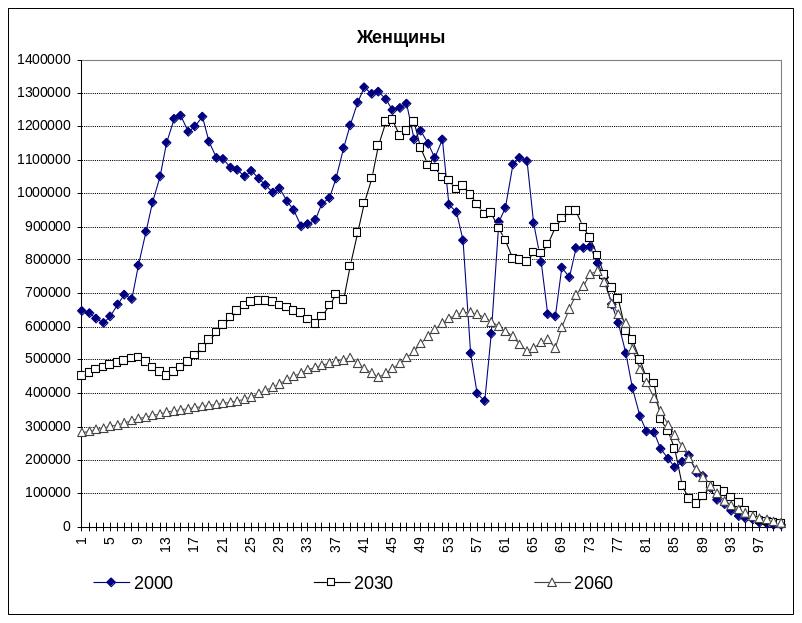
Рис. П3.5. Прогнозные распределения возрастной структуры женщин.

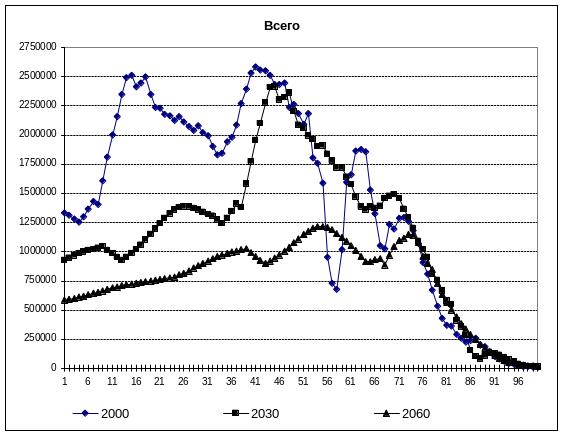
Рис. П3.6. Прогнозные распределения возрастной структуры всего населения.

Литература (к приложению 3)

1. Система знаний о народонаселении: Учеб. пособие для экон. вузов/ Д.И. Валентей, Н.В. Зверева, В.М. Медков и др.; под ред. Валентея Д.И. –/М.: Высш. школа, 1991. - 255 с. (Глава 10. Математические методы. Баркалов Н.Б.)

2. Ястремский Б.С. Связь между показателями воспроизводства населения. Избранные труды. М., 1964.

3. Венецкий И.Г. Статистические методы в демографии – /М : «Статистика», 1977 208 с. (Гомперц – Мекгейм, кривая смертности с. 191)

4. Венецкий И.Г. Математические методы в демографии – /М : «Статистика», 1975 208 с

5. Баркалов Н.Б. Моделирование демографического перехода. М., 1984.

6. Курс демографии./Под ред. А. Я. Боярского. М, 1985.

7. Валентей Д.И., Кваша А.Я. Основы демографии. М., 1989.

8. Демографическое прогнозирование// Демография: современное состояние и перспективы развития./ Под. Ред. Проф. Д.И. Валентея. М.: 1997.

9. Keyfitz N., Applied Mathematical Demography. 1985 Ch 3 (Гиперболическая модель смертности Ж. Буржуа-Пиша)

10. Heligman L., Polard J.H., The age pattern of mortality. The Journal of the Institute of Actuaries 1980, Vol. 107, part 1, № 434.

11. Mort Pak – Life. The United Nations software package for morality measement N.Y. United Nations, 1986.

12. Rogers A., Castro L. Model migration schedules Luxemburg: ПАСА, 1981

13. Zhai Zhenwu Marteal fertility models. Population Research (China). 1987. Vol 4(1). (модифицированная модель рождаемости Коула Э. Трасселла с. 171) (Коул Э. Мак-Нейл Д. Модель рождаемости с. 167)

14. Брасс У. Об одном методе выражения закономерности смертности.- В кн. Изучение продолжительности жизни. М. 1977 с.30-93 (Brass W. Coale A.Y. The Demography of Tropical Africa. Prinseton, N.Y. 1968 Ch 3. United Nation. 1983).

15. Медков В. М. Демография. Учебник. – М.: ИНФРА-М, 2004. 576 с. – (Классический университетский учебник).

16. Шахотько Л.П., Привалова Н.Н. Демографическая безопасность: сущность, задачи, система показателей и механизм реализации./ М.: Вопросы статистики, №7 2001. с. 16-21