Модуль 2. Статистические методы изучения связей и зависимостей

Тема 5. Средние величины и показатели вариации.

1. Сущность средних в статистике.

2. Средняя арифметическая, ее свойства и техника исчисления.

3. Средняя гармоническая.

4. Мода и медиана.

5. Показатели вариации.

1. Сущность средних в статистике.

Средние величины играют особую роль в статистическом исследовании. Это определяется задачей статистики – выявлением закономерностей массовых явлений. Закономерности можно выявить, лишь обобщая однородные явления и давая обобщенную характеристику единицам явлений.

Средней величиной в статистке называется обобщающая характеристика совокупности однотипных явлений по какому-либо варьирующему признаку, которая показывает уровень признака, отнесенный к единице совокупности.

Основополагающим условием применения средних величин является массовость изучаемого явления. Только при этом условии они покажут общую тенденцию, лежащую в основе процесса в целом, и покажут ее типичный для данного периода уровень проявления.

К прочим условиям верного и экономически грамотного использования средних величин относятся:

• использование средней только в том случае, когда признак изменяется, варьирует у отдельных единиц совокупности;

• средние величины могут рассчитываться только в качественно однородных совокупностях.

Средние величины, будучи обобщающими показателями, для совокупности в целом затушевывают количественные различия изучаемого признака у отдельных единиц. Поэтому даже в пределах качественно однородной совокупности нередко нужно общие средние дополнять исчислением групповых средних, так как общие средние величины могут не раскрыть подлинных закономерностей изучаемых процессов.

Введем следующие условные обозначения:

Х	Варианта признака – значение, величина признака отдельных единиц;
F	Частота – величина, которая показывает сколько раз встречается признак с такой величиной в совокупности;
	Среднее значение признака в совокупности.

Наиболее часто в практике встречаются средние арифметические и средние гармонические.

2. Средняя арифметическая, ее свойства и техника исчисления.

Средняя арифметическая используется в вариационном ряду распределения, где имеются частоты и варианты признака. Средняя арифметическая рассчитывается как:

1. Средняя арифметическая простая. Применяется когда частоты вариант равны между собой или равны единице.

=

- среднее значение признака в совокупности;

- сумма вариант признака;

n - количество частот.

Пример: определить среднюю цену на сахар за год, если средняя цена в первом квартале составила 2,50; во втором – 2,45; в третьем – 2,70; в четвертом – 2,60. Так как частоты равны единице, то используется средняя арифметическая простая:

грн.

2. Средняя арифметическая взвешенная. Используется, в случае, когда варианты совокупности имеют различную частоту.

=

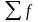- сумма всех частот в совокупности;

- общий объем значений частот варианты в совокупности.

Частоты отдельных вариант могут быть выражены не только абсолютными величинами, но и относительными значениями – частностями (w).

=

Пример: определить среднюю заработную плату работников магазина, если 1 человек получает 500 грн.; 3 – 450; 7 – 350; 2 – 250; 1 – 200. Так как варианты имеют различную частоту, то необходимо использование средней арифметической взвешенной:

грн.

В случае, когда варианты и частоты в интервальном вариационном ряду имеют большое численное значение, расчет среднего значения требует существенных усилий. Для сокращения трудоемкости расчетов использует некоторые особенности средней арифметической, позволяющие оптимизировать процесс расчета среднего значения и имеющие название способ моментов.

При расчете средней арифметической способом моментов необходимо:

1. Перейти от интервального ряда к дискретному путем нахождения среднего значения каждого интервала.

2. Вычесть из всех вариант постоянное число (лучше для этого использовать значение серединной варианты или варианты с наибольшей частотой) – A.

3. Разделить варианты на постоянное число, а именно величину интервала – i.

4. Рассчитать среднюю арифметическую из новых вариант или так называемый момент первого порядка.

M₁ =

5. Для определения величины средней арифметической нужно величину момента первого порядка умножить на величину того интервала, на который делили все варианты, и прибавить к полученному произведению величину варианты, которую вычитали.

= i x M + A

Пример: на основании приведенных данных о результатах анализа жирности молока определить среднее значение.

Жирность молока, %	Количество	Жирность молока, %	х – А (А = 3)	Х1 = (х – А)/i (i – 1)
0,5 – 1,5	12	1	- 2	- 2
1,5 – 2,5	25	2	- 1	- 1
2,5 – 3,5	38	3	0	0
3,5 – 4,5	5	4	1	1

М₁ =

%

Для проверки, произведем расчет среднего процента жирности молока, используя среднюю арифметическую взвешенную: