Задание к работе

1. Измерить разницу между высотами 1 и 2 импульсов при различных временах задержки. Если на осциллографе не виден первый импульс, то измерять , где  – высота импульса в момент, когда она перестанет меняться с увеличением времени задержки (т.е. станет равной ).

2. То же самое проделать при нагреве до 50 °С.

3. Построить график ln( ) в зависимости от времени задержки и по котангенсу угла наклона определить время жизни при комнатной температуре и при 50 °С (рис. 5).

Рис. 5. График зависимости ln( )от времени задержки импульса

4. По формуле (3) рассчитать диффузионную длину.

5. Результаты измерений занести в таблицу.

Температура T1, T2	Время задержки, мкс	U1, В	U2, В	ΔU = U1 – U2, В	ln ΔU

Контрольные вопросы

1. Физическая сущность метода модуляции проводимости.

2. Определение неосновных неравновесных носителей, их времени жизни и диффузионной длины.

3. Зависимость времени жизни от температуры.

4. Каким образом связаны τ и L?

5. Почему в полупроводниковых приборах определяющими являются параметры неосновных носителей?

Лабораторная работа № 7

ОПРЕДЕЛЕНИЕ ОБЪЕМНОЙ ДЛИНЫ ДИФФУЗИИ НЕОСНОВНЫХ НОСИТЕЛЕЙ ЗАРЯДА МЕТОДОМ ФОТОГАЛЬВАНОМАГНИТНОГО ЭФФЕКТА

Цель и содержание работы

Определение объемной длины диффузии неосновных носителей заряда методом фотогальваномагнитного эффекта.

Теоретическое введение

Пусть однородный полупроводник с проводимостью, близкой к собственной, облучается светом, как показано на рис 1.

Error: Reference source not found

Рис. 1. Схема диффузии электронно-дырочных пар при освещении

При световой генерации носителей в приповерхностном слое образуется одинаковое число электронов и дырок. Так как коэффициент диффузии у электронов больше, чем у дырок, то электроны будут быстрее диффундировать к неосвещенной грани образца. Нижняя, неосвещенная сторона образца, зарядится отрицательно, а верхняя, освещенная, – положительно. Возникшая фотоэдс (эдс Дембера) ускоряет движение дырок и замедляет движение электронов к неосвещенной стороне образца. Уравнение, описывающее движение электронно-дырочных связанных пар имеет вид

, (1)

где – коэффициент диффузии дырок; – коэффициент диффузии электронов; – подвижность электронов и дырок; – напряженность поля в направлении ; – концентрации электронов и дырок.

. (2)

Так как при световой генерации пар , можно считать, что

(3)

и

. (4)

Подставив полученное значение (4) в выражение для потока дырок, получим

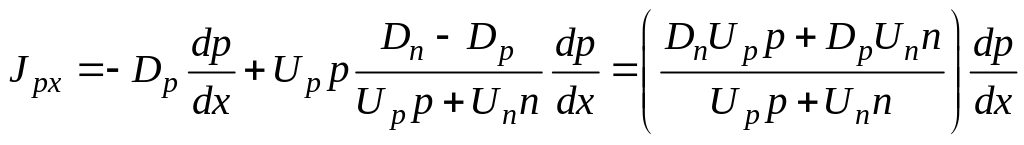      . (5)

Выражение в скобках имеет размерность и смысл коэффициента диффузии. Оно легко приводится к виду

. (6)

Коэффициент D называется коэффициентом амбиполярной диффузии.

С помощью этого коэффициента выражение для электронного диффузионного тока будет записано как

, (7)

где g – заряд электрона; – концентрация неосновных носителей.

В этой записи эдс Дембера уже неявно учтена коэффициентом .

В сильнолегированных полупроводниках коэффициент амбиполярной диффузии превращается в коэффициент диффузии неосновных носителей заряда. Действительно, если в формуле (1) , то . С другой стороны, если уровень инжекции очень высок, то даже в легированном материале процессы описываются амбиполярным коэффициентом диффузии. Если в темноте , но , то поэтому и . и подобно собственному полупроводнику

.

Для определения объемной длины диффузии используется фотогальваномагнитный эффект, суть которого состоит в следующем.

Если освещенный с одной стороны образец поместить в магнитное поле, то возникает поперечный эффект, обусловленный отклонением диффундирующих носителей магнитным полем. Этот эффект был впервые открыт в 1934 году П.К. Кикоиным и М.М. Носковым и носит название фотогальваномагнитного (ФГМ) эффекта. Обратимся к рис. 2. Так как при освещении образца на верхней освещенной грани генерируется больше пар, чем в объеме, то возникает градиент концентрации неравновесных носителей (рис. 2). Электроны и дырки диффундируют в глубь образца и отклоняются магнитным полем в направлении Y. Возникающую таким путем разность потенциалов можно рассматривать как эффект Холла на диффузионном токе.

Существенно, что в отличие от эффекта Холла электроны и дырки отклоняются магнитным полем в противоположные стороны. При этом возникает некоторый ток в направлении Y.

Error: Reference source not found

Рис. 2. Схема фотогальваномагнитного эффекта

Электронная и дырочная составляющие этого тока могут быть записаны в виде

, (8)

, (9)

где – магнитная индукция в направлении .

Суммарный ток в направлении равен .

. (10)

Плотность тока будет неодинаковой на освещенной и затемненной гранях. У верхней грани образца определяется суммой плотности тока, вызываемого полем , и тока, возникающего при отклонении диффузионных токов и магнитным полем. Эта вторая часть почти равна нулю у нижней грани образца, так как там очень мал диффузионный ток . У нижней грани ток соответствует полю Е_y. Распределение тока для режима холостого хода показано на рис. 3.

У верхней, освещённой грани образца, протекает магнитодиффузионный ток, т.е. ток, возникающий при отклонении в магнитном поле носителей, диффундирующих в направлении . Это составляющая в уравнении (10).

У нижней, неосвещённой грани, преобладает дрейфовый ток, созданный полем, – составляющая в уравнении (10). Из сказанного ясно, что . Более строго было показано, что в режиме холостого хода

и . (11)

Здесь – толщина образца.

Рис. 3. Распределение тока для режима холостого хода

Применяя эти условия к уравнению (10), получим

. (12)

Выражения для диффузионных токов возьмём в виде (7).

В этом случае

. (13)

С учётом того, что удельное сопротивление

,

выражение для напряжённости поля холостого поля примет вид

. (14)

Для определения объемного времени жизни применяется метод одновременного измерения ФГМ-эффекта и фотопроводимости (ФП), позволяющий исключить влияние поверхностной рекомбинации на освещенной поверхности и не требующий измерения освещенности образца. Для этого через образец при наличии света и магнитного поля пропускается еще постоянный ток J такого направления, чтобы напряжение, обусловленное фотопроводимостью, было противоположно по знаку напряжению ФГМ-эффекта, и подбирается при атом такая величина этого тока J, чтобы напряжение ФГМ было скомпенсировано напряжением ФП.

Напряжение ФГМ эффекта равно

, (15)

здесь – длина освещённой части образца.

Напряжение фотопроводимости , где – изменение сопротивления, вызванное освещением образца. Очевидно, что всегда выполняется соотношение

,

где – темновое сопротивление освещённой части образца. Изменение проводимости при освещении вычисляется стандартным образом:

.

Темновая проводимость образца равна

.

Таким образом,

и ,

где S – поперечное сечение образца.

На основании сказанного, напряжение фотопроводимости U_фп можно записать:

. (16)

Для определения объёмного времени жизни создаются условия, при которых распределение избыточной концентрации носителей в объёме полупроводника имеет вид

. (17)

Здесь – концентрация неравновесных носителей на освещённой грани; L – диффузионная длина.

Это выражение справедливо при соблюдении следующих условий.

1. Генерация пар происходит только на поверхности образца.

Выполнение этого условия обеспечивается водяным фильтром. Слой воды толщиной около 1 см поглощает почти все инфракрасное излучение длиннее 1 мк; прошедшее коротковолновое излучение генерирует носители в очень тонком приповерхностном слое Ge, много меньшем диффузионной длины.

2. Толщина образца должна в 2–3 раза превышать диффузионную длину. Только в этом случае распределение неравновесных носителей не будет зависеть от скорости поверхностной рекомбинации на неосвещенной стороне образца.

При равенстве напряжений ФП и ФГМ . Учитывая формулы (14), (15), (16), (17), можно получить:

. (18)

После сокращения имеем: , и окончательно получим:

. (19)

При измерениях необходимо следить за тем, чтобы световое пятно было на расстоянии 5–4 диффузионных длин от торцевых контактов, которые должны быть невыпрямляющими. При несоблюдении этого условия возможны ошибки из-за фотоэдс, возникающих в контактах металл–полупроводник.