2.3 Осевые реакции

При установке вала на двух радиальных шариковых подшипниках осевая сила z₁ или z_2, нагружающая подшипник, равна внешней осевой силе , действующей на вал. Силу воспринимает тот подшипник, который ограничивает осевое перемещение вала под действи­ем этой силы. На рисунке 3,а силу воспринимает подшипник в опоре 1, на рисунке 2 (а, б) — фиксирующая опора.

В случае установки вала на двух однорядных радиально-упорных подшипниках при приложении радиальной нагрузки R появляется осевая составляющая , возникающая в подшипнике из-за наклона контактной линии:. .

для шарикоподшипников (5)

для роликоподшипников (6)

где е и е' — соответственно коэффициенты осевого нагружения и минимальной осевой нагрузки.

Для шарикоподшипников коэффициент е' зависит от угла контакта:

при (7)

при (8)

где - статическая грузоподъёмность подшипника (прил. 1.9).

При и определяется по табл. 1. Учитывая, что для радиально-упорных роликоподшипников выражение (6) можно представить в следующем виде:

(9)

Осевая нагрузка z₁ и z₂, на радиально-упорные однорядные подшипники при их парной установке на валу определяется исходя из внешней осевой нагрузки , возникающей в зацеплении зубчатых колес, и осевых составляющих и радиальных нагрузок R₁ и R₂ в опорах 1 и 2.

Таблица 1

Коэффициенты радиальной и осевой динамических нагрузок

Подшипник	Угол контакта	Относительная нагрузка,					е
			X	Y	X	Y
Шариковый радиальный одно и двухрядный	0	0,014 0,028 0,056 0,084 0,11 0,17 0,28 0,42 0,56	1	0		2,30/2,30 1,99/1.99 1,71/1,71 1,55/1,55 1,45/1,45 1,3/1,31 1,15/1,15 1,04/1,04 1,00/1,00	0,19 0,22 0,26 0,28 0,30 0,34 0,38 0,42 0,44
Шариковый радиально-упорный	12	0,014 0,029 0,057 0,086 0,11 0,17 0,29 0,43 0,57	1	2,08/0 1,84/0 1,69/0 1,52/0 1,39/0 1,3/0 1,2/0 1,16/0 1,16/0	0,74/0,46	2,94/1,81 2,63/1,62 2,37/1,46 2,18/1,34 1,98/1,22 1,84/1,13 1,69/1,04 1,64/1,01 1,62/1	0,3 0,34 0,37 0,41 0,45 0,48 0,52 0,54 0,54
Роликовый конический	-	-	1	0,45	0,67/0,4	0,67/0,4	1,5
Шариковый упорно-радиальный	45 60 75	- - -	1,18 1,90 3,89	0,59 0,54 0,52	0,66/0,66 0,92/0,92 1,66/1,66	1/1 1/1 1/1	1,25 2,17 4,67
Роликовый радиально-упорный	-	-	1,5	0,67		1,1	1,5

Примечание. В числителе приведены значения X и Y для двухрядных подшипников, а в знаменателе — для однорядных.

Для нормальной работы радиально-упорных подшипников необходимо, чтобы в каждой опоре осевая сила, нагружающая подшипник, была не меньше минимальной:

и (10)

Кроме того, должно быть выполнено условие равновесия вала — равенство нулю суммы всех осевых сил, действующих на вал. Например, для схемы на рисунке 5 имеем:

(11)

В представленной на рисунке 5 расчетной схеме обозначены: и - внешняя осевая и радиальная нагрузки, действующие на вал; R₁ и R₂ - радиальные реакции опор; z₁ и z₂, — осевые реакции опор.

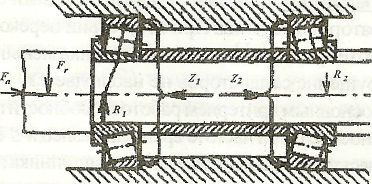
Рис. 5 Одна из схем иагружения вала и опор с радиально-упорными регулируемыми подшипниками

Для нахождения осевых реакций применяют метод попыток, предварительно осевую силу в одной из опор принимая равной минимальной.

Попытка 1: пусть, например, . Тогда из условия равновесия вала имеем

Проверяем выполнение условия для второй опоры. Если при этом , то осевые силы найдены правильно. Если (что недопустимо), то нужно предпринять вторую попытку.

Попытка 2: примем . Тогда из условия равновесия вала имеем

При этом условие обязательно выполняется.