Тема: нелінійна парна регресія
Лабораторна робота № 3
ЗАВДАННЯ:
На основі статистичних даних побудувати графік. Визначити, до якого виду належить регресійна залежність.
Звести нелінійну парну регресію до лінійної парної регресії.
Визначити індекс кореляції та коефіцієнт детермінації.
Використовуючи критерій Фішера, з надійністю
оцінити адекватність прийнятої
економічної моделі статистичним даним.Якщо модель адекватна статистичним даним, то знайти:
з надійністю надійні зони базисних даних;
точкову оцінку прогнозу;
з надійністю інтервальну оцінку прогнозу;
оцінки коефіцієнтів еластичності для базисних даних і прогнозу;
Побудувати графіки статистичних даних, лінії регресії і її довірчої зони, коефіцієнта еластичності.
На основі одержаної економетричної моделі зробити висновки.
Методичні вказівки до виконання роботи
Визначити вигляд емпіричної формули для таблиці
X |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
Y |
12 |
35 |
75 |
125 |
210 |
315 |
445 |
600 |
800 |
Будуємо графік
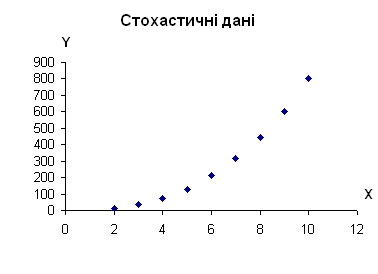
По
вигляду ця функція належить до степеневих
.
Проведемо лінеаризацію регресії.
Введемо наступні заміни:
,
,
.
Отримаємо
лінійну функцію
.
За
допомогою статистичної функції LINEST
(ЛИНЕЙН) визначимо
показники лінійної регресії
;
.
Проводимо зворотну заміну:
;
.
Отримаємо
степеневу залежність
.
Вводиться гіпотеза, що між фактором х та показником y існує стохастична залежність
Визначимо
індекс кореляції
:
=0,9999.
Коефіцієнт (індекс) детермінації визначається по формулі:
=0,988.
Для оцінки адекватності прийнятої економетричної моделі експериментальним даним використовуємо критерій Фішера. Перевіримо гіпотезу про статистичну незначність рівняння регресії..
5,59
(де
,
,
).
Розрахуємо надійні зони базисних даних для кожного показника y:
середня стандартна помилка ,
де
;
гранична помилка
;надійний інтервал
.
Точкова
оцінка прогнозу для
.
Середня
стандартна помилка
=
4,7.
Гранична
помилка
=11,12.
Надійний
інтервал
.
Розрахуємо коефіцієнт еластичності:
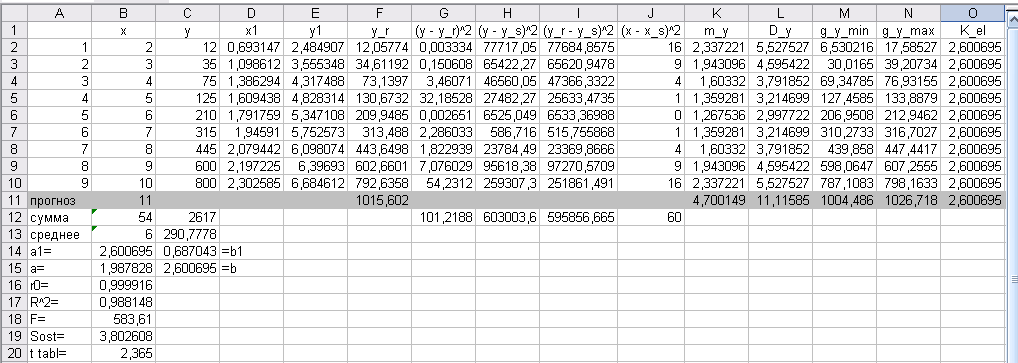
Для наочного уявлення одержаних розрахунків на окремому листі будуємо графіки фактичних даних (y), лінії регресії для базисних даних та прогнозу (y_r), довірчу зону для базисних даних і прогнозу (g_y_min, g_y_max), коефіцієнта еластичності (К_еl).
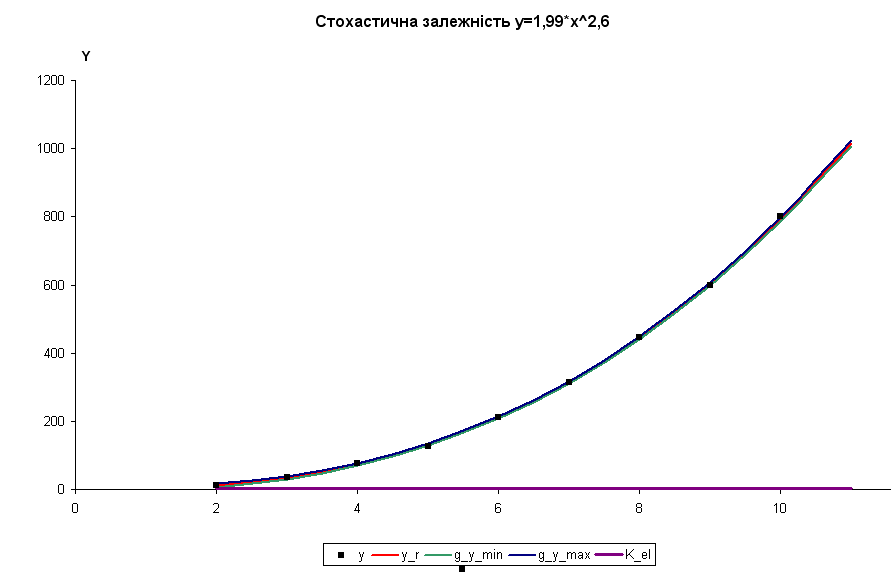
Далі на окремому листі по кожному пункту роботи треба зробити аналіз та економічні висновки.
Варіанти для самостійного виконання
Значення фактора, показнику і прогнозу показнику
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
||||||||
X |
Y |
X |
Y |
X |
Y |
X |
Y |
X |
Y |
X |
Y |
X |
Y |
X |
Y |
1,01 |
12,0 |
1,02 |
3,02 |
1,10 |
1,84 |
1,08 |
4,37 |
1,10 |
2,72 |
5,12 |
6,50 |
9,35 |
8,68 |
0,21 |
0,19 |
1,51 |
8,84 |
1,59 |
2,94 |
1,55 |
2,22 |
1,53 |
4,01 |
1,33 |
2,91 |
10,6 |
7,17 |
15,3 |
9,86 |
0,69 |
0,47 |
2,02 |
6,99 |
2,12 |
2,71 |
2,09 |
3,54 |
2,05 |
3,29 |
1,58 |
3,18 |
15,1 |
7,39 |
20,7 |
10,7 |
1,03 |
0,67 |
2,51 |
6,03 |
2,61 |
3,32 |
2,52 |
3,50 |
2,58 |
3,10 |
1,81 |
3,50 |
21,4 |
7,85 |
26,5 |
11,2 |
1,38 |
0,66 |
3,01 |
5,55 |
3,05 |
2,69 |
3,07 |
5,30 |
3,02 |
3,22 |
2,09 |
3,71 |
27,3 |
8,01 |
33,1 |
11,9 |
1,71 |
0,92 |
3,49 |
5,12 |
3,56 |
2,99 |
3,57 |
5,42 |
3,58 |
2,99 |
2,32 |
3,88 |
32,8 |
8,20 |
39,4 |
12,3 |
2,07 |
1,00 |
3,98 |
4,63 |
4,00 |
3,22 |
4,05 |
7,12 |
4,06 |
2,90 |
2,59 |
4,06 |
37,1 |
8,23 |
44,5 |
12,6 |
2,47 |
1,15 |
4,48 |
4,41 |
4,50 |
3,42 |
4,56 |
8,27 |
4,56 |
2,37 |
2,85 |
4,18 |
45,2 |
8,49 |
50,7 |
12,9 |
2,92 |
1,39 |
4,99 |
4,01 |
5,03 |
4,00 |
5,06 |
8,71 |
5,01 |
1,87 |
3,14 |
4,39 |
49,3 |
8,57 |
56,0 |
13,2 |
3,38 |
1,48 |
5,49 |
3,96 |
5,56 |
3,43 |
5,53 |
10,1 |
5,51 |
1,82 |
3,43 |
4,44 |
55,1 |
8,53 |
63,0 |
13,4 |
3,87 |
1,72 |
5,97 |
3,70 |
6,04 |
4,49 |
6,06 |
11,3 |
6,06 |
1,89 |
3,69 |
4,55 |
60,2 |
8,65 |
68,8 |
13,7 |
4,23 |
1,85 |
6,47 |
3,75 |
6,50 |
4,44 |
6,50 |
12,4 |
6,52 |
2,28 |
3,90 |
4,63 |
67,2 |
8,67 |
75,0 |
13,9 |
4,64 |
1,94 |
6,98 |
3,72 |
7,01 |
4,83 |
7,00 |
13,2 |
7,02 |
1,46 |
4,20 |
4,61 |
75,4 |
8,84 |
81,4 |
14,1 |
5,00 |
2,11 |
7,51 |
3,53 |
7,58 |
4,62 |
7,54 |
14,7 |
7,53 |
1,56 |
4,42 |
4,66 |
82,2 |
8,83 |
87,9 |
14,2 |
5,50 |
2,32 |
7,99 |
3,25 |
8,04 |
5,01 |
8,00 |
15,5 |
8,05 |
1,73 |
4,72 |
4,66 |
89,2 |
9,01 |
93,9 |
14,4 |
5,98 |
2,45 |
8,45 |
|
8,52 |
|
8,53 |
|
8,48 |
|
4,99 |
|
94,4 |
|
100 |
|
6,32 |
|
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
||||||||
X |
Y |
X |
Y |
X |
Y |
X |
Y |
X |
Y |
X |
Y |
X |
Y |
X |
Y |
0,32 |
2,44 |
0,32 |
45,7 |
0,38 |
48,3 |
0,11 |
1,78 |
1,03 |
1,27 |
1,15 |
5,44 |
1,01 |
5,02 |
9,33 |
9,67 |
0,93 |
3,62 |
0,93 |
5,97 |
0,93 |
7,97 |
0,39 |
2,22 |
1,63 |
1,42 |
1,64 |
7,01 |
1,35 |
5,51 |
15,7 |
11,8 |
1,59 |
4,98 |
1,59 |
3,82 |
1,61 |
4,60 |
0,66 |
4,30 |
2,16 |
1,93 |
2,28 |
10,6 |
1,71 |
6,52 |
20,9 |
13,8 |
2,29 |
5,43 |
2,29 |
3,27 |
2,35 |
4,02 |
0,89 |
5,49 |
2,71 |
2,35 |
2,77 |
13,4 |
2,09 |
7,92 |
26,7 |
13,5 |
2,92 |
5,59 |
2,92 |
3,06 |
3,02 |
3,75 |
1,15 |
6,57 |
3,26 |
2,73 |
3,42 |
17,4 |
2,49 |
9,64 |
32,0 |
15,0 |
3,62 |
5,94 |
3,62 |
2,86 |
3,63 |
3,72 |
1,43 |
7,15 |
3,77 |
3,93 |
3,78 |
21,7 |
2,85 |
10,1 |
38,0 |
16,7 |
4,30 |
6,67 |
4,30 |
2,79 |
4,35 |
3,33 |
1,67 |
10,5 |
4,35 |
5,12 |
4,49 |
28,6 |
3,28 |
14,1 |
44,6 |
16,4 |
4,99 |
9,62 |
4,99 |
2,63 |
5,02 |
3,27 |
1,95 |
12,5 |
4,91 |
6,55 |
5,08 |
35,7 |
3,64 |
19,2 |
51,3 |
17,9 |
5,63 |
11,4 |
5,63 |
2,54 |
5,72 |
2,67 |
2,23 |
17,5 |
5,50 |
9,05 |
5,63 |
41,4 |
4,04 |
25,6 |
58,2 |
19,9 |
6,25 |
12,6 |
6,25 |
2,60 |
6,25 |
3,26 |
2,45 |
24,2 |
6,01 |
12,2 |
6,11 |
49,5 |
4,47 |
32,6 |
64,6 |
20,5 |
6,90 |
14,0 |
6,90 |
2,41 |
6,99 |
2,55 |
2,72 |
32,0 |
6,60 |
17,3 |
6,79 |
60,0 |
4,83 |
37,0 |
71,3 |
20,0 |
7,56 |
17,8 |
7,56 |
2,47 |
7,59 |
2,89 |
2,93 |
41,7 |
7,20 |
25,3 |
7,39 |
68,9 |
5,20 |
48,0 |
77,5 |
22,3 |
8,21 |
21,3 |
8,21 |
2,41 |
8,30 |
2,44 |
3,13 |
52,0 |
7,78 |
36,2 |
7,84 |
76,8 |
5,70 |
61,1 |
84,4 |
22,3 |
8,91 |
25,8 |
8,91 |
2,50 |
9,00 |
2,92 |
3,41 |
73,8 |
8,35 |
52,8 |
8,48 |
89,8 |
6,02 |
70,6 |
90,9 |
23,3 |
9,57 |
30,3 |
9,57 |
2,45 |
9,64 |
2,89 |
3,63 |
95,5 |
8,90 |
76,2 |
8,57 |
92,5 |
6,52 |
88,6 |
96,3 |
22,7 |
10,2 |
|
10,2 |
|
10,2 |
|
3,85 |
|
9,42 |
|
9,46 |
|
6,90 |
|
103 |
|
Форма стохастичної залежності
1 |
|
2 |
|
3 |
|
4 |
|
5 |
|
6 |
|
7 |
|
8 |
|
9 |
|
10 |
|
11 |
|
12 |
|
13 |
|
14 |
|
15 |
|
16 |
|
