Электрон и его свойства

Электрон, открытый Дж. Дж. Томсоном (1897), является одной из основных атомных частиц материального мира. Электроны входят в состав всех атомов, образуя их электронные оболочки.

Состояние электрона, входящего в состав одной из разрешённых для данного атома оболочек, называют связанным. Связанный электрон, хотя и находится в непрестанном, хаотичном движении теплового характера, но покинуть свой атом не может, т.к. ему не хватает собственной энергии для преодоления сил притяжения к ядру. Такие электроны не могут перемещаться направленно, поскольку связаны со своим атомом, поэтому вещества со связанными электронами в обычных условиях не могут проводить электрический ток, и являются диэлектриками (изоляторами).

Вместе с тем, многие вещества, находясь в обычных условиях, могут проводить электрический ток, и потому их называют проводниками. Электроны таких веществ, - а это валентные электроны, электроны внешней электронной оболочки, испытывают настолько слабое притяжение к ядру, в силу своей удалённости от него, что даже при температуре абсолютного нуля имеют собственную – т. н. начальную энергию, достаточную для ухода от своего атома. Такие электроны называют свободными – свободными от атома, но не от вещества. Концентрация свободных электронов в медном проводнике даже при температуре абсолютного нуля не меньше концентрации атомов – 10²⁸м^-3 и, как известно, растет с ростом температуры.

Промежуточное положение по величине проводимости занимают полупроводники. У них электроны связаны с ядром значительно слабее, чем у диэлектриков, но существенно сильнее, чем у проводников. По этой причине при температуре абсолютного нуля полупроводники ведут себя как диэлектрики, т.е. электрический ток в них при наложении электрического поля отсутствует, но в обычных условиях они обретают свойство проводить электрический ток, хотя это свойство гораздо менее выражено, чем у проводников. Например, в обычных условиях концентрация свободных электронов у германия составляет 10¹⁹м^-3. Следовательно, число свободных электронов в германии по отношению к числу атомов составляет 10 ^-7%, в то время как у меди число свободных электронов (электронов проводимости) не меньше числа атомов, т.е. минимум 100%.

Совокупность таких (свободных) электронов часто называют электронным газом, поскольку электроны ведут себя как атомы и молекулы газа, находясь в непрестанном движении.

Как известно, в проводниках при любой температуре все атомы ионизованы, т.е. их валентные электроны потеряли свою связь с атомами. С точки зрения зонной теории это объясняется тем, что зона проводимости и валентная зона в энергетической диаграмме вещества смыкаются и даже перекрывают друг друга. Поэтому, даже при температуре абсолютного нуля электроны имеют настолько большую энергию, что покидают свои атомы и становятся свободными от них, разрывая парноэлектронные (ковалентные) связи между атомами. Количество таких свободных (от атомов) электронов не менее количества атомов в рассматриваемом объеме вещества. Поведение этих электронов напоминает поведение газа, т.е. их движение носит хаотичный характер, интенсивность которого тем выше, чем выше температура вещества. В такой ситуации в узлах решетки располагаются только ионы, говорят – ионная решетка «плавает» в электронном «газе». Вещество при этом в целом сохраняет свою электрическую нейтральность, поскольку количество положительных зарядов (ионов) равно количеству делокализованных (от лат. локус – место) электронов, т.е. электронов, потерявших свое «место» в парноэлектронных связях.

Скорость хаотичного движения свободных электронов достаточно велика: при комнатной температуре она имеет величину порядка 10⁴м/с. Можно предположить, что какой-то электрон, находящийся вблизи поверхности, будет иметь вектор мгновенной скорости, ориентированный в направлении «из вещества», и станет у даляться от него. Данная ситуация представлена на рис.1.1а, на котором изображен разрез части вещества проводника, ограниченного ломаной линией, с плоской эмитирующей поверхностью (вертикальная прямая). Кружками со знаком «минус» обозначены делокализованные электроны, а кружками со знаком «плюс» - ионы.

Однако, как только электрон покинет вещество, нейтральность того микрообъема вещества, в котором электрон находился (на рисунке заштрихован), будет нарушена, и данный микрообъем приобретет положительный заряд. В соответствии с законом Кулона электрон будет испытывать притяжение к указанному микрообъему, его кинетическая энергия начнет уменьшаться, и он вернется обратно, удалившись от вещества на одно-два межатомных расстояния. При этом электрическая нейтральность микрообъёма будет восстановлена, что создаст условия для выхода за пределы вещества следующего электрона. Похожая ситуация имеет место в случае с камнем, брошенным вертикально вверх. Двигаясь вверх в гравитационном поле, камень будет замедлять своё движение, его кинетическая энергия будет уменьшаться, а потенциальная – расти. И как только его кинетическая энергия движения вверх станет равной нулю, камень начнёт возвращаться на землю.

Отсюда следует, что в обычных условиях, под которыми понимают отсутствие энергетических воздействий на вещество и отсутствие внешнего – по отношению к веществу – силового поля (ракета покидает Землю, если тяга двигателей превышает силу тяжести), покинувшие вещество электроны вновь возвращаются в него. Поскольку таких, временно покинувших вещество, электронов достаточно много, то вблизи поверхности эмиттера образуется электронная как бы «оболочка» со своим объёмным или пространственным зарядом (рис.1.1б). Она неоднородна: поскольку электроны в веществе распределены по энергиям в соответствии со статистикой Ферми, то те из них, которые имеют наибольшую энергию, удаляются от поверхности эмиттера на наибольшее же расстояние (d на рис. 1.1б) электроны же с минимальной энергией удаляются, соответственно, на минимальное расстояние. Поскольку и тех и других гораздо меньше, чем электронов со средними значениями энергий, то в середине «оболочки» концентрация электронов больше, чем на периферии.

Таким образом, по обе стороны поверхности вещества эмиттера имеет место двойной электрический слой, представленный совокупностями положительных (ионы) и отрицательных (электроны) зарядов. Следовательно, на данном промежутке возникает электрическое поле ε_б, силовые линии которого изображены на рис. 1б. При попадании в это поле, электроны испытывают на себе действие силы, стремящейся вернуть их в вещество. Как следствие, их кинетическая энергия уменьшается, а потенциальная растёт по некоторому закону U(x), Максимальное значение этой энергии, необходимое для удаления от поверхности вещества на расстояние, на котором уже не действуют возвращающие силы, называется вакуумным уровнем и обозначается как U₀.

Возвращающая сила F_в возникает уже тогда, когда частица начинает покидать «свой» микрообъём, двигаясь к поверхности вещества и входя в область двойного электрического слоя, - т.е. при . Затем она достигает максимума при и становится равной нулю при (рис.1.1). Если полагать, что ширина приповерхностной области вещества, занятой положительными ионами, составляет , то изменение потенциальной энергии частицы найдётся как

.

Примерный вид графика потенциальной функции изображён пунктирной линией на рис.1.2.

Для упрощения расчётов по оценке вероятности выхода электрона за пределы вещества будем полагать, что ( т.е. будем уменьшать ширину двойного электрического слоя так, чтобы

.

При этом получим скачкообразное изменение от нуля до в точке , т.е. будет иметь вид потенциальной ступени или потенциального порога (на рис.1.2 заштрихован).

В обычных условиях полная энергия электрона, находящегося в веществе – E<U₀. поэтому с точки зрения классической физики электрон, двигаясь к поверхности вещества, должен отразиться от потенциального порога. С точки зрения квантовой механики существует конечная вероятность того, что электрон, имеющий энергию меньшую «высоты» порога, может углубиться в него на некоторое расстояние х.

Т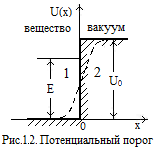 аким образом, потенциальная функция в упрощенном виде:

Подобное упрощение допустимо при условии, что ширина двойного электрического слоя много меньше длины волны де-Бройля.

Стационарное уравнение Шрёдингера для одномерного случая (рассматривается не зависящее от времени распределение плотности вероятности только по координате х) и для области 2 рис.1.2. имеет вид:

(1.1)

где = (x) – волновая функция, зависящая от координаты (пси малое), m – масса покоя электрона, - постоянная Планка, – «высота» потенциального порога (вакуумный уровень), E – полная энергия электрона в веществе.

Выражение (1.1) представляет собой однородное линейное дифференциальное уравнение второго порядка. Такие уравнения, как известно, решают с помощью подстановки:

(x)=exp(kx), (1.2)

где k– модуль волнового вектора.

Дифференцируя функцию (1.2), получим:

(x) , (x) . (1.3)

Подстановка выражений (1.2),(1.33) в уравнение (1.1) приводит (опуская промежуточные вычисления) к уравнению Шрёдингера для области 2 рис.1.2 (

(1.4)

где

Для области 1 рис.1.2, ( :

(1.5)

где

Решая уравнения (1.4), (1.5), находят волновые функции для указанных областей, после чего производят их «сшивание» (пси-функция должна быть гладкой и непрерывной), приравнивая сами функции и их первые производные в точке В итоге волновая функция для области 2:

(1.6)

а для области 1:

1.7)

где - амплитуда падающей (на потенциальный порог в направлении оси x) волны, - начальная фаза волны в области

Анализ (1.6) и (1.7) показывает, что слева от порога ( волновая функция представляет собой стоячую волну, а справа от него ( имеет место апериодический затухающий процесс. Кроме того, при

Полученные выражения позволяют оценить вероятность проникновения частицы за потенциальный порог, т.е. вероятность её локализации в области В указанной области координаты частицы распределены с плотностью:

(1.8)

Анализ выражения (8) показывает, что вероятность локализации частицы хотя и спадает в области по экспоненте, однако она отлична от нуля при любом значении x и обращается в нуль лишь при

Возьмём отношение функций распределения для областей 1 и 2 рис.1.2:

Если, например, , то для электронов

Оценим вероятность проникновения электрона в потенциальный порог на глубину :

Следовательно, вероятность обнаружения электрона на расстоянии 0,1нм от границы потенциальной ступени составляет 30% от вероятности его локализации на самой границе, т.е. из ста электронов, обладающих энергией E, тридцать из них удалятся от границы раздела на расстояние 0,1нм.

Таким образом, вопреки представлениям классической физики электрон можно обнаружить за пределами вещества. Однако, в итоге он всё равно вернётся обратно, не в силах преодолеть действие возвращающих сил. Что касается эмиссии электронов, то она возможна лишь при выполнении определённых условий: либо превращение потенциального порога в потенциальный барьер, при котором возможно туннелирование электронов, либо сообщение электронам дополнительной – к уже имеющейся у них – энергии, что позволит им совершить работу против сил, удерживающих электроны в веществе. Эту дополнительную энергию называют работой выхода. Работу выхода, измеряемую обычно в электронвольтах, определяют как разность между вакуумным уровнем и уровнем собственной энергии электрона в веществе и обозначают часто как еφ, где е – заряд электрона, а φ – так называемый потенциал выхода, В.

Надо полагать, что при оценке возможности эмиссии необходимо учитывать максимальную собственную энергию электрона. Как известно, максимальная энергия электрона при температуре абсолютного нуля называется энергией (или уровнем) Ферми и обозначается как Е_F. Следовательно, минимальная энергия, необходимая для удаления самого «быстрого» электрона равна U₀ E_F. При Т ˃ 0 в металле появляются электроны на уровнях, которые выше уровня Ферми, но и в этом случае работу выхода отсчитывают от уровня Е_F, т.к. последний мало меняется в широком диапазоне температур. Например, работа выхода вольфрама при 3000К составляет 4,5эВ, а при температуре абсолютного нуля – 4,52эВ. Следовательно, уровень Ферми является характеристическим параметром вещества. Таким образом, работа выхода

(1.9)

также является параметром вещества, величина которого меняется в небольших пределах в зависимости от температуры, состояния поверхности вещества и др. факторов.

В зависимости от того, какого вида энергия сообщается веществу эмиттера, различают фотоэлектронную, термоэлектронную, вторичную, взрывную и др. электронные эмиссии. Существует также автоэлектронная эмиссия, которая имеет место без сообщения электронам дополнительной энергии и поэтому является специфическим видом эмиссии, основанном на квантовомеханическом явлении – туннельном эффекте и связанным с ним эффекте Шоттки.

Возникает вопрос – что будет происходить с электроном после осуществления эмиссии? Приведенные ранее примеры практического применения вакуумных приборов предполагают возможность управления электронными потоками. Но, если исходить из принципа неопределенности (соотношения неопределенностей) Гейзенберга (СНГ), то мы не можем говорить о каком-то определенном поведении электрона и о его траектории. Согласно данному принципу, неопределенность (иначе говоря – ошибка) в определении координаты х электрона при одномерном его движении в направлении оси х – и неопределенность его импульса могут быть найдены из следующего выражения:

(1.10)

где ,– неопределенность импульса электрона в направлении х (проекция неопределенности p на ось х), - постоянная Планка. Из приведенного выражения следует, что получить одновременно точные значения координаты и импульса электрона невозможно, т.к. рост точности определения импульса неминуемо влечет за собой уменьшение точности определения координаты (h - константа) и наоборот.

Однако поведение электронов в вакуумном межэлектродном промежутке электровакуумных приборов существенно отличается от поведения их в веществе, и ограничениями, накладываемыми соотношением неопределенностей (1.10), можно пренебречь.

Данное положение наиболее наглядно можно проиллюстрировать, рассматривая движение электронов в таком вакуумном люминесцентном приборе как электронно-лучевая трубка (ЭЛТ). Этот прибор предназначен для преобразования электрических сигналов в видимое изображение, которое формируется на экране – тонком слое вещества – люминофора, светящегося при бомбардировке его пучком электронов, который называют лучом (откуда и название прибора). Светящаяся точка на экране трубки является элементом отображения (ЭО), часто её называют «пикселем». Изображение формируется в результате периодических возвратно-поступательных перемещений ЭО по экрану. Диаметр ЭО является важным параметром прибора – чем он меньше, тем более детальным будет изображение. В свою очередь, диаметр ЭО определяется диаметром пучка электронов. Оценим возможность использования для электронов понятия траектории, используя схему, приведенную на рис.1.3.

Обозначим символом ℓ расстояние от источника электронов до экрана, а символом δ радиус ЭО. Если для реальных условий работы окажется много меньше δ, то расчет траектории электронов можно осуществлять на основе классической физики, используя законы Ньютона. Источником электронов является так называемый электронный прожектор (ЭП), испускающий разогнанный в электрическом поле анода пучок электронов, полученных в процессе термоэлектронной эмиссии, перпендикулярно плоскости экрана в центр ЭО. В результате электроны приобретают импульс р₀ , который при отсутствии неопределенности был бы ориентирован аналогично. Вследствие наличия неопределенности реальное значение импульса - находится как векторная сумма (на рисунке). Будем полагать, что «разброс» импульса по плоскости экрана равновероятен, поэтому можно рассматривать одномерный случай, используя только ось x. На практике у ЭЛТ радиус ЭО δ 10^-5м, длина ℓ 10^-1м. Разгоняющее электроны анодное напряжение имеет величину порядка 10⁴В. Направим ось x вертикально в плоскости экрана. Из подобия прямоугольных треугольников с катетами и δ следует: ≈ δ/ℓ ≈ 10^-4, где p – импульс электрона, который он получил при своем движении к экрану. В соответствии с законом сохранения энергии:

где m_e – масса покоя электрона, – напряжение на участке анод – эмиттер, v – скорость электрона. Отсюда . С учетом приведенного значения разгоняющей разности потенциалов:

p м/c.

Следовательно, ≈ р м c, и согласно (1.10) / м/c) Таким образом, поскольку то электрон является управляемым объектом. Для него существует понятие координаты и траектории, и его движение можно рассчитывать по законам классической механики, а значит, и создавать потоки электронов (пучки) различной конфигурации и менять их направление, воздействуя на электроны электрическим и (или) магнитным полями. Например, в тех же ЭЛТ или электронных микроскопах электронные пучки сжимают до размеров почти геометрической точки.

1.3. Автоэлектронная и взрывная эмиссии. Эффект Шоттки

Поскольку, как было установлено, электроны могут удаляться от вещества, в котором они находятся, на некоторое расстояние, то, создавая в области их локализации внешнее электрическое поле, можно этим полем удалить их от вещества и получить, тем самым, эффект электронной эмиссии.

Такое поле можно создать с помощью внешнего – по отношению к веществу эмиттера – электрода. На этот электрод, называемый анодом, необходимо подавать относительно вещества эмиттера напряжение такой полярности, чтобы электрическое поле между ними действовало встречно полю Ɛ_б, образованному двойным электрическим слоем (рис.1.1). Его ширина, при этом, уменьшится за счёт наиболее энергичных электронов, находящихся на большем расстоянии от эмиттера и увлекаемых анодным полем ε_а в направлении к аноду. Таким образом, произошло уменьшение высоты потенциального порога и создались условия для преобразования его в потенциальный барьер, через который, как известно, электроны могут «туннелировать», т.е. преодолевать его, несмотря на то, что высота барьера по-прежнему остаётся больше энергии электронов.

Подобная эмиссия носит название «автоэлектронной». Тер-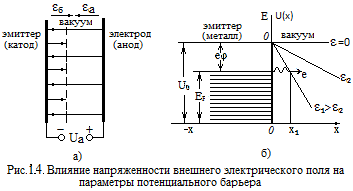

мин «автоэлектронная эмиссия» означает, что выход электронов за пределы эмиттера происходит самопроизвольно, без затраты дополнительной внешней энергии, и электроны, преодолевшие барьер, приобретают энергию в вакуумном промежутке эмиттер-анод от электрического поля Ɛ_а.

Чем больше напряжённость внешнего электрического поля Ɛ_а, тем в большей степени с изменением расстояния x происходит увеличение потенциальной энергии электрона в этом поле. Тем уже потенциальный барьер (рис.1.4б), а следовательно, большее количество электронов со всё меньшими уровнями собственной энергии уходят на анод, увеличивая плотность тока эмиссии, а значит, и анодного тока (тока на анод).

Явление трансформации потенциального порога в барьер и уменьшения высоты барьера, что приводит к росту автоэмиссионного тока, носит название эффекта Шоттки.

Для получения значительных эмиссионных токов необходима напряжённость анодного поля порядка 10⁷-10⁹ В/м. Существенные токи автоэмиссии можно получить при небольших анодных напряжениях, создавая неоднородные анодные поля. Такое поле имеет место, например, если катод имеет форму иглы. При этом на острие велика концентрация силовых линий анодного поля, что предопределяет высокую напряжённость поля на нём.

Электрическое поле у поверхности твёрдого тела может быть образовано не только за счёт внешней разности потенциалов, ускоряющей электроны от катода к аноду, но также за счёт поля положительных ионов, находящихся у поверхности катода. Такой слой ионов, к примеру, может появиться за счёт испарения части вещества автоэмиссионного катода при его нагреве собственным автоэмиссионным током. Ионизация испарившихся атомов приводит к созданию у поверхности катода слоя плотной неравновесной газоразрядной плазмы. Сильное электрическое поле в пограничной области эмиттер-плазма вызывает дополнительное усиление автоэлектронной эмиссии, приводящее к аномально высоким плотностям эмиссионного тока. Этот процесс носит резкий, взрывной характер и, как правило, заканчивается вакуумным пробоем (дугой), зачастую приводящей к разрушению электродов. Процесс перехода от нормальной автоэлектронной эмиссии к вакуумной дуге получил название взрывной эмиссии.