6. Алгебра высказываний (Алгебра Буля). Таблицы истинности.

Основным математическим аппаратом, используемым при анализе и синтезе дискретных элементов и устройств является алгебра логики (булева алгебра, алгебра Буля). В алгебре логики широко используется понятие “высказывание”.будем называть простое повествовательное положение, о котором можно сказать, что оно ложно или истинно, но не то и другое одновременно. Любое высказывание можно обозначить символом X и считать, что X=1, если высказывание истинно, а X=0, если высказывание ложно. Логическая (булева) переменная – такая переменная X, которая может принимать только два значения: X={0,1}. Из двух простых высказываний X1 и X2 можно образовать более сложные высказывания, используя операции “И”, “ИЛИ”, “НЕ”. Сложные высказывания также принимают значения “истинно” или “ложно”, т.е. 1 или 0. Смысл логических операций над простыми высказываниями X1 и X2 и значениями сложных высказываний можно представить в виде таблиц истинности: “ИЛИ”, “И”, “НЕ” соответственно.

Алгебра логики — это раздел математики, изучающий высказывания, рассматриваемые со стороны их логических значений (истинности или ложности) и логических операций над ними.

Алгебра логики возникла в середине ХIХ века в трудах английского математика Джорджа Буля. Ее создание представляло собой попытку решать традиционные логические задачи алгебраическими методами.

Логическое высказывание — это любое повествовательное пpедлoжение, в oтнoшениикoтopoгo можно oднoзначнo сказать, истинно oнo или лoжнo.

Предложения типа "в городе A более миллиона жителей", "у него голубые глаза" не являются высказываниями, так как для выяснения их истинности или ложности нужны дополнительные сведения: о каком конкретно городе или человеке идет речь. Такие предложения называются высказывательными формами.

Высказывательная форма — это повествовательное предложение, которое прямо или косвенно содержит хотя бы одну переменную и становится высказыванием, когда все переменные замещаются своими значениями.

Алгебра логики рассматривает любое высказывание только с одной точки зрения — является ли оно истинным или ложным.

Употребляемые в обычной речи слова и словосочетания "не",   "и",   "или",  "если... , то",   "тогда и только тогда" и другие позволяют из уже заданных высказываний строить новые высказывания. Такие слова и словосочетания называются   логическими связками.

Высказывания, образованные из других высказываний с помощью логических связок, называются   составными. Высказывания, не являющиеся составными, называются   элементарными.

Так, например, из элементарных высказываний "Петров — врач", "Петров — шахматист" при помощи связки "и" можно получить составное высказывание "Петров — врач и шахматист".

При помощи связки "или" из этих же высказываний можно получить составное высказывание "Петров — врач или шахматист", понимаемое в алгебре логики как "Петров или врач, или шахматист, или и врач и шахматист одновременно".

Истинность или ложность получаемых таким образом составных высказываний зависит от истинности или ложности элементарных высказываний.

Алгебра высказываний

В алгебре высказываний суждениям (высказываниям) ставятся в соответствие логические переменные (заглавные буквы латинского алфавита). Рассмотрим два простых высказывания:

А - «Два умножить на два равно четырем».

В - «Два умножить на два равно десяти».

Высказывания, как уже говорилось ранее, могут быть истинными или ложными. Истинному высказыванию соответствует 1, ложному 0, в нашем случае первое высказывание истинно (А = 1), а второе ложно (В=0).

В алгебре высказываний над высказываниями можно производить определенные логические операции, в результате которых получаются новые, составные высказывания. Истинность полученных составных высказываний зависит от истинности входящих в него простых высказываний и использованных при преобразовании логических операциях.

Для образования новых высказываний наиболее часто используются логические операции, выражаемые словами «и», «или», «не».

Логическое умножение (конъюнкция)

Объединение двух (или нескольких) высказываний в одно с помощью союза «и» называется операцией логического умножения или конъюнкцией.

Составное высказывание, образованное в результате конъюнкции, истинно тогда и только тогда, когда истинны входящие в него простые высказывания.

Операцию логического умножения (конъюнкцию) принято обозначать либо значками «», «&», либо знаком умножения «*». Образуем составное высказывание С, которое получится в результате конъюнкции двух высказываний: С = А В.

Истинность такого высказывания задается специальной таблицей, таблицей истинности логического умножения:

А	В	АВ
0	0	0
0	1	0
1	0	0
1	1	1

Логическое сложение (дизъюнкция)

Объединение двух (или нескольких) высказываний с помощью союза «или» называется операцией логического сложения или дизъюнкцией.

Составное высказывание, образованное в результате дизъюнкции, ложно тогда, когда одновременно ложны входящие в него простые высказывания.

Операцию логического сложения (дизъюнкцию) принято обозначать либо значком «», либо знаком сложения «+». Образуем составное высказывание С, которое получится в результате дизъюнкции двух простых высказываний: С =AВ

Истинность такого высказывания задается специальной таблицей, таблицей истинности логического сложения:

А	В	АВ
0	0	0
0	1	1
1	0	1
1	1	1

Логическое отрицание (инверсия)

Присоединение частицы «не» к высказыванию называется операцией логического отрицания или инверсией.

Инверсия делает истинное высказывание ложным и наоборот.

Операцию логического отрицания (инверсию) над логическим высказыванием А принято обозначать . Образуем высказывание С, являющееся логическим отрицанием .

С =

Истинность такого высказывания задается специальной таблицей, таблицей истинности логического отрицания:

А
0	1
1	0

При преобразовании логических выражений определено следующее старшинство логических операций: инверсия, конъюнкция, дизъюнкция (для изменения указанного порядка могут использоваться скобки).

Построим таблицу истинности для логического выражения /\ :

А	В			/\
0	0	1	1	1
0	1	1	0	0
1	0	0	1	0
1	1	0	0	0

Построим теперь таблицу истинности для логического выражения :

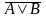А	В	АВ
0	0	0	1
0	1	1	0
1	0	1	0
1	1	1	0

Таблицы истинности совпадают, следовательно, логические выражения равносильны: /\ =

Логические элементы компьютера оперируют с сигналами, представляющими собой электрические импульсы. Есть импульс - логическое значение сигнала 1, нет импульса - значение 0.

Пример:

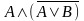
А	В
И	И	И	Л	Л
И	Л	И	Л	Л
Л	И	И	Л	Л
Л	Л	Л	И	Л

Самой «сильной» логической связкой является отрицание, затем идут связки конъюнкция, дизъюнкция, а самыми «слабыми» являются связки импликации и эквиваленции.

Таким образом, простые высказывания являются переменными, а более сложные высказывания – функциями. Причем как переменные, так и функции могут принимать только значения 0 или 1. Алгебра логики может быть определена как алгебра, содержащая 3 операции “И” (конъюнкция), “ИЛИ” (дизъюнкция), “НЕ”(отрицание) над множеством элементов, каждый из которых принимает два значения 0 или 1. Результаты выполнения операций над множеством элементов также принимают два значения 0 или 1. Рассмотрим следующий пример. Допустим, принимается некоторое решение коллективом из 3-х лиц, которые обозначим a, b, c. Решение считается принятым, если “за” не менее 2-х человек. Процесс принятия решений может быть представлен следующей таблицей истинности.

Таблица истинности

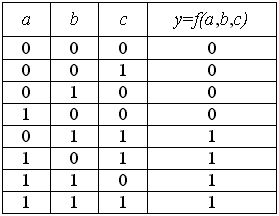Исходя из таблицы истинности, получим следующие функцию алгебры логики (ФАЛ), которая является сложным высказыванием и является математической моделью принятия решения:

Алгебра логики содержит ряд аксиом и правил. Среди них основными являются следующие:

Таблица основных логических равенств

1. закон двойного отрицания

2. 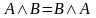коммутативность конъюнкции

3. 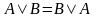коммутативность дизъюнкции

4. ассоциативность конъюнкции

5. 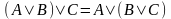ассоциативность дизъюнкции

6. 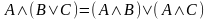закон дистрибутивности

7. закон дистрибутивности

8. 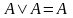закон идемпотентности

9. закон идемпотентности

10.

11.

12.

13.

14.

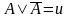
15.

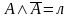
16 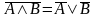закон де Моргана

17. 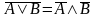закон де Моргана

18.

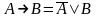
19.

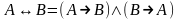
20.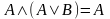 закон поглощения

21. закон поглощения