3.3.2 Пример №2

Для уравнения уточнить значение корня методом хорд.

Производная равна:

Решим квадратное уравнение:

Корни этого квадратного уравнения: x₁=0; x₂= -4; x₃= 1.

-∞	-4	0	1	∞
+	-	-	-	+

Сузим интервалы:

-6	-4	1	4
+	-	-	+

Интервалы будут следующими: [-6;-4] и [1,4]. Подставим данные в программу:

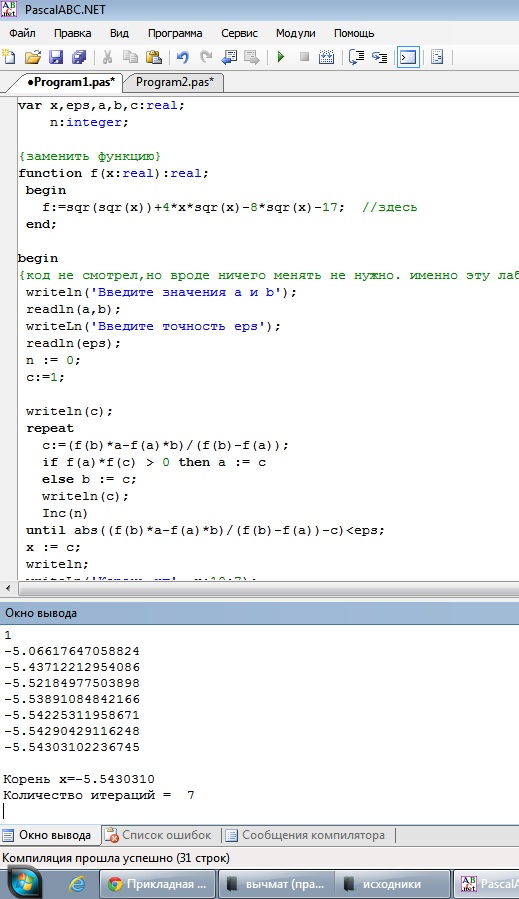
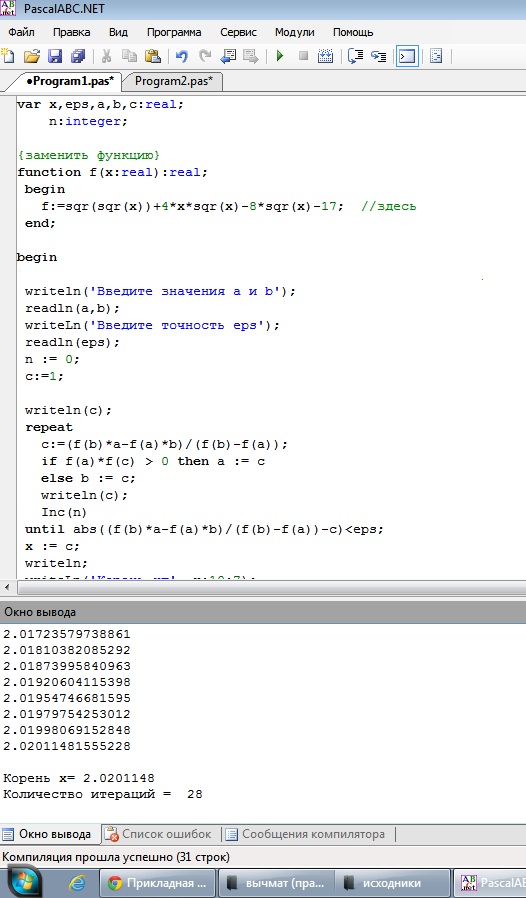
Рис. 2. Скриншоты решения примера №2

Ответ: на полученных интевалах для уравнения содержится 2 корня:

3.4 Уточнение корней с заданной точностью объединенным методом

3.4.1 Пример №1

Решить уравнение объединенным методом

Рис. 1. Графики функций 0.5^x-3 = (х+2)²

Интервал для нахождения корней: [-2;1]. Подставим полученные значения в программу:

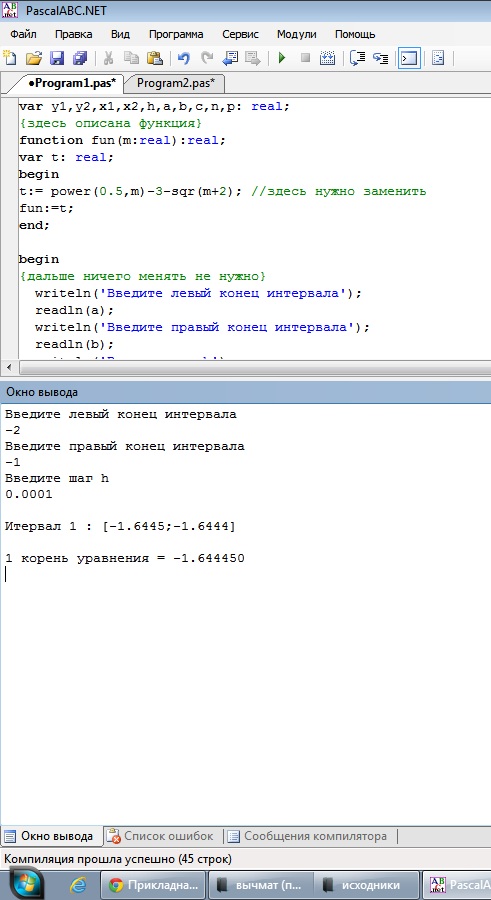
Рис. 2. Скриншот решения примера №1

Ответ: на интервале [-2;1] уравнение имеет корень х₁ = -1.644

3.4.2 Пример №2

Решить уравнение объединенным методом

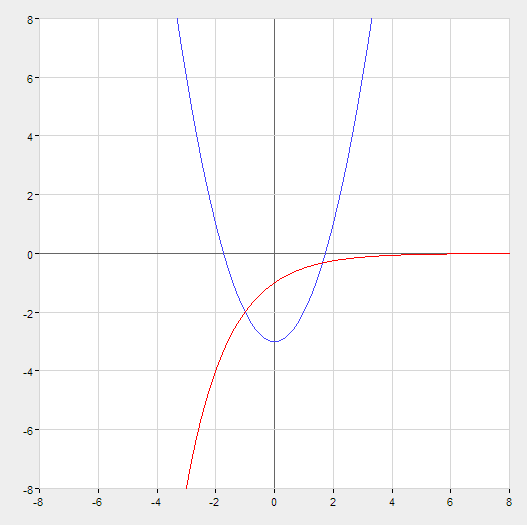
Рис. 3 Графики функций x²– 3 и -0.5^x

Выделим 2 интервала, содержащих корни: [-2;0] и [0;2]. Подставим полученные значения в программу:

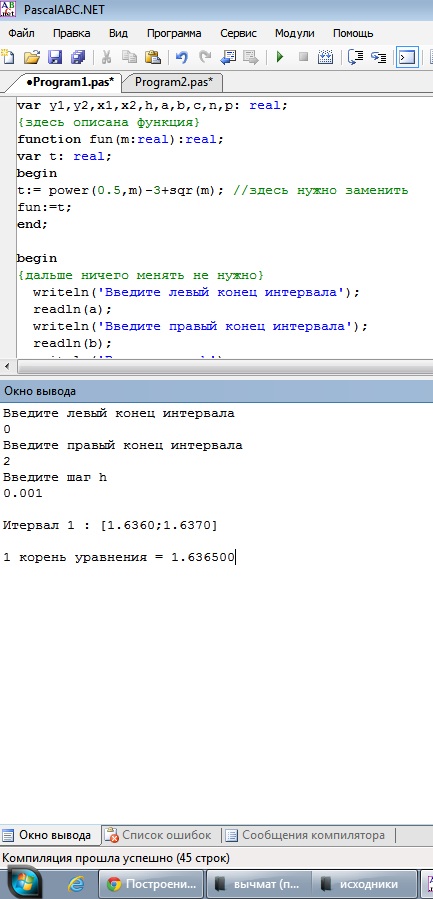
Рис. 4. Скриншот решения примера №2

Ответ: на интервале [-2;0] уравнение имеет корень х₁ = -0.999; интервале [0;2] уравнение имеет корень х₂ = 1.637

3.5 Уточнение значения изолированного корня методом касательных

3.5.1 Пример №1

Для уравнения уточнить значение корня методом касательных.

Производная равна:

Решим квадратное уравнение:

Корни этого квадратного уравнения: x₁=0; x₂= -4; x₃= 1.

-∞	-4	0	1	∞
+	-	-	-	+

Сузим интервалы:

-6	-4	1	4
+	-	-	+

Интервалы будут следующими: [-6;-4] и [1,4]. Подставим данные в программу:

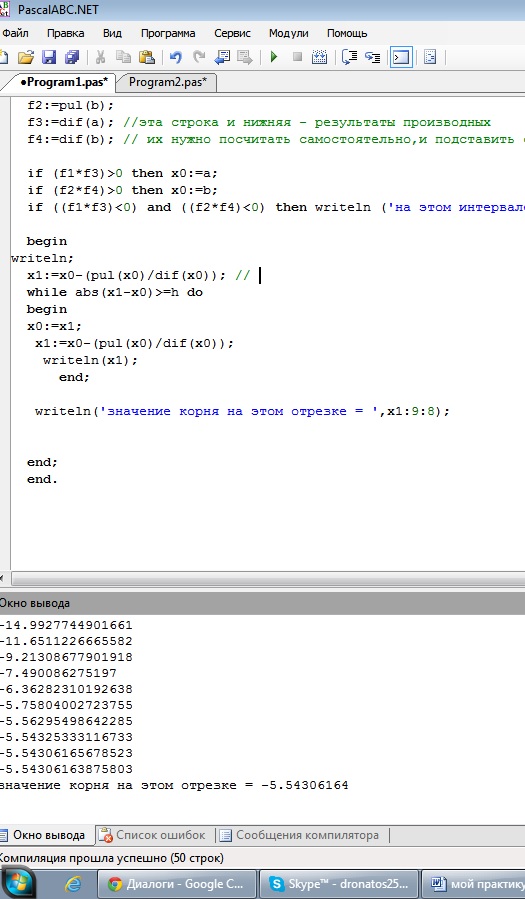
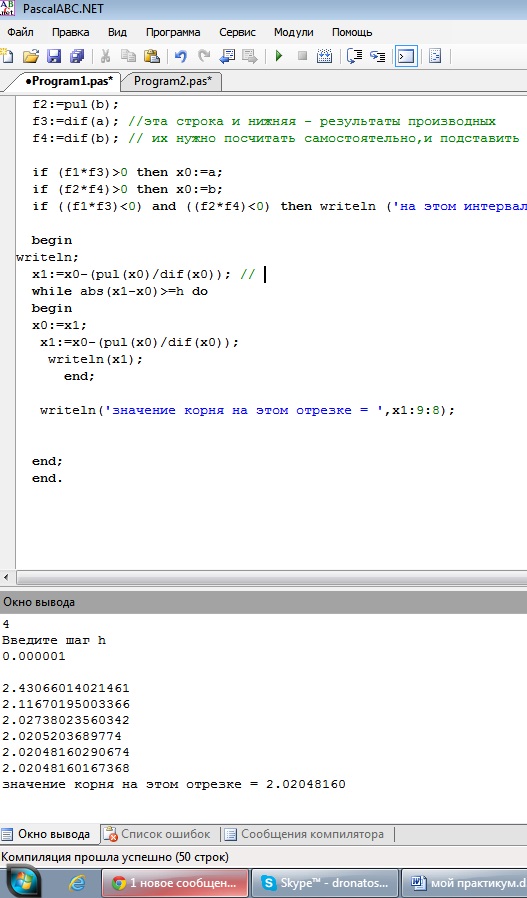
Рис. 1. Скриншоты решения примера №1

Ответ: на полученных интевалах для уравнения содержится 2 корня:

3.5.2 Пример №2

Для уравнения уточнить значение корня методом касательных.

Производная равна:

Решим квадратное уравнение:

Корни уравнения: x₁=0; x₂= -0.5; x₃= 0.5;

-∞	-0.5	0	0.5	∞
+	-	-	-	+

Сузим интервалы:

-2	-0.5	0.5	2
+	-	-	+

Интервалы будут следующими: [-2;-0,5] и [0,5;2]. Подставим данные в программу:

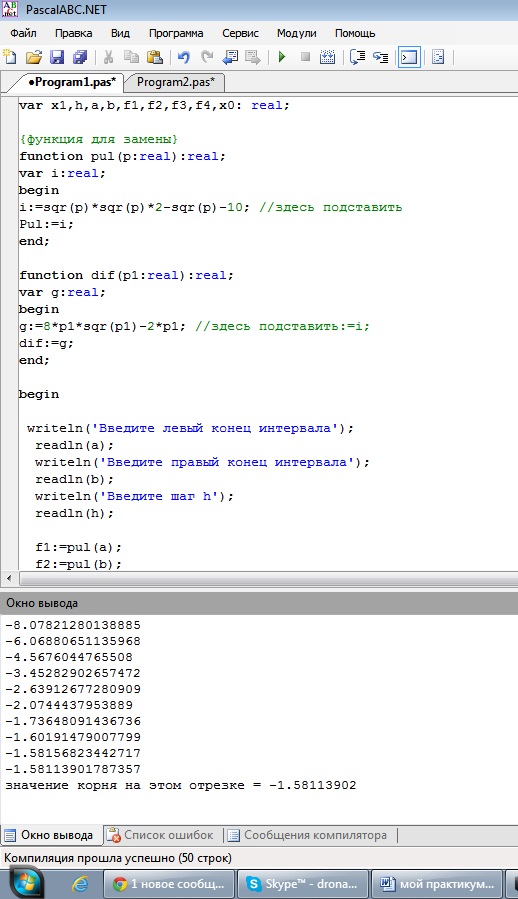
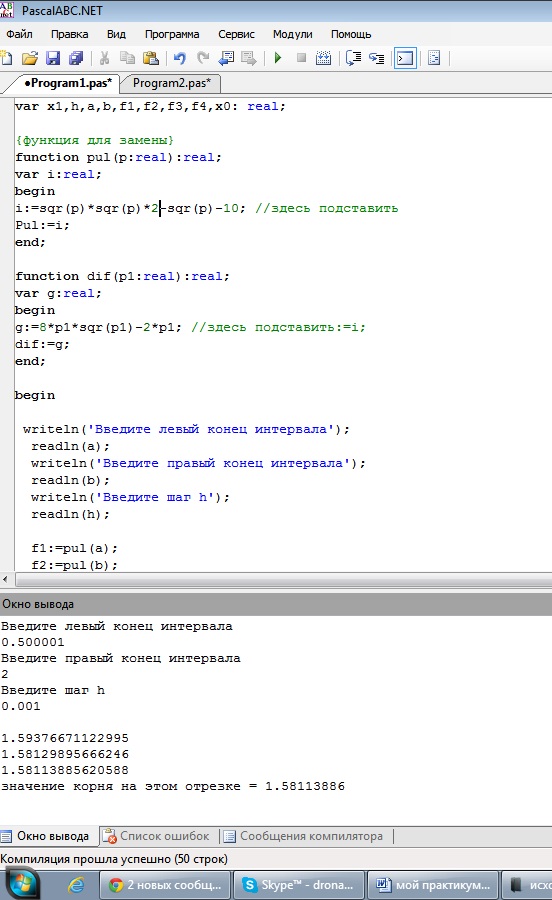
Рис. 2. Скриншоты решения примера №2

Ответ: на полученных интевалах для уравнения содержится 2 корня:

3.6 Уточнение значения изолированного корня методом простых итераций

3.6.1 Пример №1

Решить следующее уравнение методом простых итераций:

Построим графики функций и отделим интервалы с корнями:

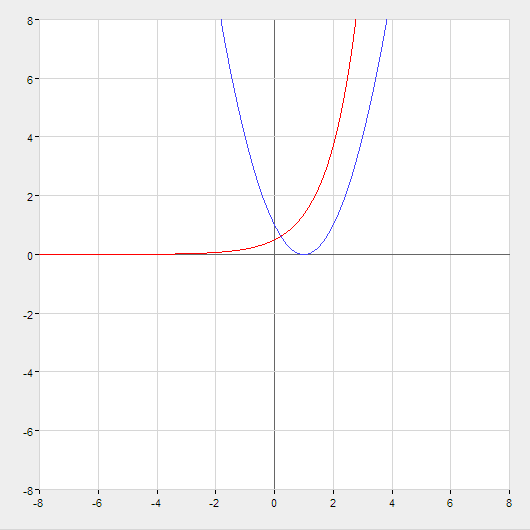
Рис. 1. Графики функций (х-1)² и е^х/2

Как видно из графиков, интервал, содержащий корень, только один: [0;2]. Подставим полученные данные в программу:

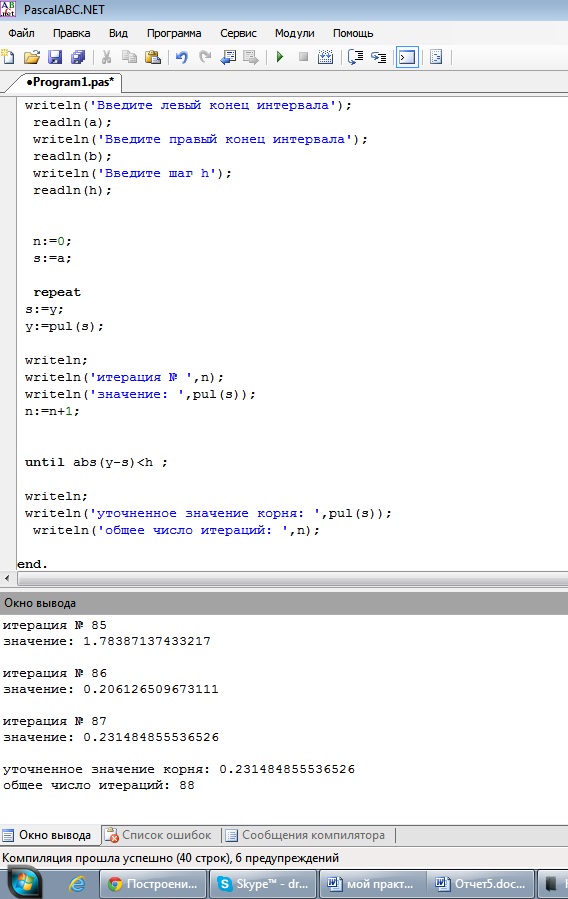
Рис. 2. Скриншот решения примера №1

Ответ: на интервале [0;2] уравнение имеет корень х = 0.231;