Министерство образования и науки Российской Федерации

ФГБОУ ВПО УРАЛЬСКИЙ ГОСУДАРСТВЕННЫЙ ЭКОНОСИЧЕСКИЙ УНИВЕРСИТЕТ

Кафедра статистики, эконометрики и информатики

Курсовая работа на тему «Нахождение значения многочлена по схеме Горнера»

Исполнитель

Студент группы ЭМА-10 Каргаполов А.В.

Руководитель Миронова Л.И.

Екатеринбург

2013

1.1 Теоретическое описание схемы Горнера 4

1.5 Скриншот решения контрольного примера 8

1.6 Описание примера №2 9

1.7 Скриншот примера №2 9

2. Презентационные материалы по методу «Схема Горнера» 10

3. Вычислительный практикум 14

3.1 Отделение изолированных корней уравнения с помощью компьютерной программы 14

3.1.1 Пример №1 14

3.1.2 Пример №2 15

3.2 Уточнение корней с заданной точностью методом дихотомии 16

3.2.1 Пример №1 16

3.2.2 Пример №2 17

3.3 Уточнение корней с заданной точностью методом хорд 19

3.3.1 Пример №1 19

3.3.2 Пример №2 20

3.4 Уточнение корней с заданной точностью объединенным методом 22

3.4.1 Пример №1 22

3.4.2 Пример №2 23

3.5 Уточнение значения изолированного корня методом касательных 25

3.5.1 Пример №1 25

3.5.2 Пример №2 26

3.6 Уточнение значения изолированного корня методом простых итераций 28

3.6.1 Пример №1 28

3.6.2 Пример №2 29

3.7 Решение систем линейных уравнений методом Гаусса 31

3.7.1 Пример №1 31

3.8 Обращение матриц методом Гаусса 32

3.8.1 Пример №1 32

3.8.2 Пример №2 33

3.9 Решение систем линейных уравнений методом простых итераций 34

3.9.1 Пример №1 34

3.9.2 Пример №2 35

3.10 Интерполирование функций 36

3.10.1 Пример №1 36

3.11 Численное интегрирование 37

3.11.1 Формула левых прямоугольников 37

Пример №1 37

3.11.2 Формула правых прямоугольников 38

Пример №1 38

3.11.3 Формула средних прямоугольников 39

Пример №1 39

3.11.4 Формула трапеций 40

Пример №1 40

Заключение 41

Список использованных источников 42

Введение

1. Схема Горнера

1.1 Теоретическое описание схемы Горнера

Схема Горнера (или правило Горнера, метод Горнера) — алгоритм вычисления значения многочлена, записанного в виде суммы мономов (одночленов), при заданном значении переменной. Метод Горнера позволяет найти корни многочлена, а также вычислить производные полинома в заданной точке. Схема Горнера также является простым алгоритмом для деления многочлена на бином вида  . Метод назван в честь Уильяма Джорджа Горнера.

Пусть задан многочлен:

.

Пусть требуется вычислить значение данного многочлена при фиксированном значении  . Представим многочлен   в следующем виде:

.

Определим следующую последовательность:

…

…

Искомое значение Р(x₀)=b₀ . Покажем, что это так.

В полученную форму записи  Р(x₀) подставим х=x₀ и будем вычислять значение выражения, начиная со внутренних скобок. Для этого будем заменять подвыражения через  :

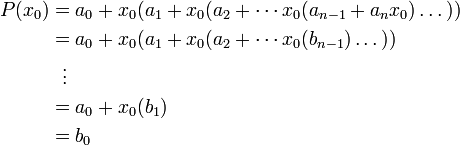
Использование схемы Горнера для деления многочлена на бином

При делении многочлена   на   получается многочлен   с остатком  ,

при этом коэффициенты результирующего многочлена удовлетворяют рекуррентным соотношениям:

,  .

При вычислениях применяют таблицу:

Таким же образом можно определить кратность корней (использовать схему Горнера для нового полинома). Так же схему можно использовать для нахождения коэффициентов при разложении полинома по степеням х-с: