Ответы и решения

1. Единицы измерения физических величин

1.14. Скорость движения 5 м/с означает, что тело каждую секунду перемещается на 5 м. Так как в одном километре 1000 м, а в часе - 3600 с, то надо скорость, выраженную в метрах в секунду разделить на 1000 и умножить на 3600:

1.15.

1.16. Давлению 101325 Па соответствует значение 760 мм.рт.ст.

Следовательно: 101325 Па ― 760 мм.рт.ст.

2·10⁵ Па ―р.

1.22. а) р₁  р₂; б) р₁= р₂; в) р₁ р₂; г) р₁  р₂.

1.23. а) V₁ = V₂ ; б) V₁  V₂; в) V₁ V₂; г) V₁ = V₂.

1.24. а) Т₁  Т₂; б) Т₁ Т₂; в) Т₁= Т₂; г) Т₁ Т₂.

1.25. а) V₁  V₂ ; б) V₁  V₂; в) V₁= V₂; г) V₁  V₂.

2. Механика

2.1. Для сложения векторов и необходимо сделать их плоскопараллельный перенос таким образом, чтобы начало обоих векторов находилось в одной точке. Затем из конца вектора провести прямую, параллельную вектору , а из конца вектора – параллельную .

В полученном параллелограмме проводится диагональ из точки начала векторов. Длина диагонали соответствует сумме + :

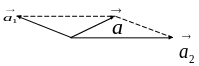
Другой вариант сложения векторов заключается в плоскопараллельном переносе начала одного вектора в конце другого. Например, начала вектора в конец вектора .

З атем из начала вектора в конец вектора проводится вектор являющийся суммой и :

2.4. Одновременное сложение трех и более векторов проводится плоскопараллельным переносом начала каждого последующего вектора в конец предыдущего (см. решение 2.1).

Затем из начала первого вектора в конец последнего проводится результирующий вектор

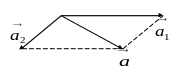
2.6. Для разложения вектора на составляющие надо из конца вектора провести прямые, параллельные указанным направления и построить параллелограмм, стороны которого будут составляющими вектора .

2.23. Примем первый поезд, в котором находится наблюдатель, в качестве неподвижной системы отсчета. Тогда скорость второго, встречного поезда относительно первого будет равна

где: V – скорость второго поезда относительно первого; V₁ и V₂ – скорости первого и второго поездов, соответственно, относительно земли.

Следовательно

где: l – начальное расстояние между поездами, τ – время движения поездов до их встречи,

где: 16,67 – скорость первого поезда относительно земли, выраженная в метрах в секунду.

Принимая, по прежнему, в качестве неподвижной системы первый поезд, получим, что второй от момента встречи локомотивов до расхождения последних вагонов должен пройти расстояние L = 2·l (см. рисунок):

Таким образом,

.

2.24.

2.25. км/ч.

2.26. км/ч.

2.27. мин = 45 с.

2.28. м/с; м/с.

Направление вектора скорости студента относительно и трамвая, и маршрутки противоположное по отношению к направлению его скорости относительно земли.

2.29. V_ст.1 = 242 м/с = 871,2 км/ч;

V_ст.2 = 238 м/с = 856,8 км/ч.

2.30. τ = 40 с; V ≈ 2,24 м/с; S = 40 м; α = 63°.

2.31. V ≈ 4,27 м/с; α ≈ 28 °.

2.32. S = 8,4 м; l = 6,8 м; V₁ = 5 см/с; V_ср ≈ 3,1 см/с.

2.33. V ≈ 30,4 м/с; α ≈ 9,5°.

2.34. h = 2,57 м; τ ≈ 2,47 с; l = 32,14 м; β ≈ 168 °.

2.35. V₀ = 15 м/с; а = 0,2 м/с².

2.36. а = 24,5 м/с²; τ ≈ 0,4 с.

2.37. h = 81,6 м; τ ≈ 4,1 с.

2.38. а = 4 м/с².

2.39. V_A = 20 м/с; τ = 20 с.

2.40. Первое тело покоится; второе – движется равномерно; пятое – движется ускоренно с монотонно изменяющимся ускорением из точки О, без начальной скорости и без начального ускорения.

2.41. V_Гал = с; V_Лор = 0,8 с.

2.42. m₁ ≈ 2002 т; m₂ ≈ 5571 т.

2.44. а = 0, так как геометрическая сумма всех действующих на тело сил равна 0.

2.49.

2.53. m ≈ 33,3 кг.

2.54. Под действием силы F₁ оба тела получают одинаковое ускорение

Нить тянет тело m₂, следовательно, сила, приложенная от нити к телу m₂, равна F₂ = m₂·a = 0,800·5 = 4 H.

По третьему закону Ньютона тело m₂ действует на нить (натягивает нить) с такой же по абсолютному значению, но противоположно направленной силой

2.55. При ускорении, направленном вверх (против ускорения свободного падения) Н.

При ускорении, направленном вниз (по ускорению свободного падения)

2.56. F_C = 3,4 H.

2.57. P_{(подъем)} = 3136 Н ≈ 3,14 кН; Р_(спуск) ≈ 3920 Н ≈ 3,92 кН.

2.58. Рис. 1. График 1 – покой; график 2 – равномерное движение из точки начала отсчета; график 4 – равномерное движение из точки, удаленной от начала отсчета на расстояние S₀; график 8 – ускоренное движение; график 9 – замедленное движение.

Рис. 2. График 1 – покой (V₀ = 0); график 4 – равноускоренное движение с начальной скоростью; график 9 – ускоренное движение с уменьшающимся ускорением, переходящее (после точки перегиба графика) в замедленное.

Рис. 3. График 1 – равноускоренное движение (а = const); график 5 – равнозамедленное движение (а = const < 0); график 6 – равномерное движение или покой.

2.59. Находясь на пятиметровой вышке, пловец обладает относительно поверхности воды потенциальной энергией За счет этой энергии он, преодолевая сопротивление воды, погружается в нее на глубину h₂ = 2м. При этом силой сопротивления совершается работа

По закону сохранения энергии U = A, или – m·g·h₁ = F_C · h₂. Тогда и откуда

2.60. А = 1475 Дж.

2.61.

2.62. V₀ = 10 м/с; F_Г ≈ 3,3 кН.

2.63. Т = 18 МДж.

2.64. m = 10 кг; h ≈ 5,1 м.

2.65.

2.66. V_б = 450 м/с. Направление движения осколка такое же, как направление движения снаряда до его разрыва.

2.67. V ≈ 1,73 м/с.

2.68. Δр₁ = m·V – 0 = 0,5 кг·м/с;

Δр₂ = m·V – (– m·V) = 1,0 кг·м/с;