Тема 10.Коническая прямозубая передача

1. Конические зубчатые колёса применяют в передачах, у которых оси валов пересека­ются под некоторым углом. Наиболее распространены передачи с углом 90 градусов. Ко­нические передачи сложнее цилиндрических в изготовлении и монтаже. Выполнить коническое зацепление с той же точностью, что и цилин­дрическое значительно труднее, пересечение осей валов затрудняет размещение опор. Од­но из конических колес, как правило, располагают консольно. При этом увеличивается не­равномерность распределения нагрузки по длине зуба. В коническом зацеплении действу­ют осевые силы, которые усложняют конструкцию опор. По опытным данным нагрузочная способность конической передачи составляет около 0,85 цилиндрической.

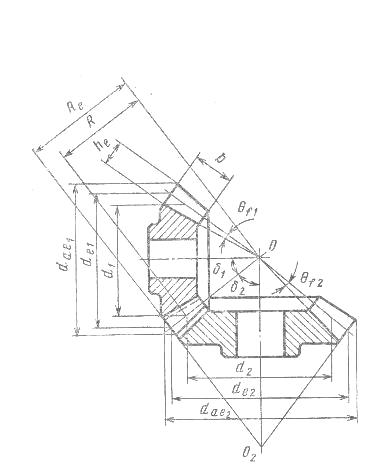
Рис.1 Коническая передача

Аналогами начальных и делительных цилиндров цилиндрических передач в кониче­ских являются начальные и делительные конусы. Конусы, образующие которых перпенди­кулярны образующим делительных конусов называют дополнительными. Сечение зубьев дополнительным конусом, называют торцевым сечением. Различают внешние, внутренние и средние торцевые сечения. Размеры, относящиеся к внешнему торцевому сечению со­провождают индексом «е». Размеры в среднем сечении - индексом «m». Ширина зубчатого венца «b». Размеры по внешнему торцу удобнее для измерения, их указывают на чертежах. Размеры в среднем сечении используют при силовых расчетах. Зависимость размеров в среднем и торцевом сечениях:

Re = R_m + 0,5b; de = d_m*Re*Rm ; m_te = m_ne * Re/Rm;

Для прямозубых конических передач торцовое «t» и нормальное «n» сечения совпада­ют. При этом m_te = m_ne округляют до стандартного. Для выполнения силовых расчетов ис­пользуют приведение прямозубого конического колеса к эквивалентному прямозубому ци­линдрическому. Форма зуба конического колеса в нормальном сечении дополнительным конусом такая же как у цилиндрического прямозубого колеса. Эквивалентное цилиндриче­ское колесо получается как развертка дополнительного конуса.

2. Геометрические параметры конической прямозубой передачи

Z₁ и Z₂ - Число зубьев шестерни и колеса

∑ = 90⁰ - Межосевой угол передачи

Z_c= √ (Z₁²+Z₂²) - Число зубьев плоского колеса

R_e=0,5m_{e *} Z_c - Внешнее конусное расстояние

m_e= h_e / 2,2 - Внешний окружной модуль

h_e=h_ae+ h_f = 2,2m_e - Внешняя высота зуба

h_ae = m_e - Внешняя высота головки зуба

R_m = R_e - 0,5b - Среднее конусное расстояние

b - Ширина зубчатого венца , b ≤ 0,3 _* R_e ; b≤10m_e

m_m = m_{e *} R_m/R_e Средний окружной модуль

d_m1 = m_{m *} Z₁ ; d_m2 = m_{m *} Z₂ - Средний делительный диаметр

δ₁ , δ₂ - Угол делительного конуса

tgδ₁ = Z₁ / Z₂; δ₂ = 90⁰ – δ₁; sinδ₁ = cosδ₂;

u = Z₂ / Z₁ - Передаточное число

S_e = 0,5_*π_*m_e - Внешняя окружная толщина зуба

θ_f - Угол ножки зуба

tgθ_f = h_f / R_e

θ_a - Угол головки зуба

θ_a = θ_f

δ_a - Угол конуса вершин

δ_a1 = δ₁ + θ_{a ,} δ_a2 = δ₂ - θ_a

δ_f - Угол конуса впадин

δ_f1 = δ₁ + θ_f , δ_f2 = δ₂ – θ_f

d_e - Внешний делительный диаметр

d_e1 = m_e*Z₁ , d_e2 = m_e*Z₂

d_ae - Внешний диаметр вершин зубьев

d_ae1 = d_e1 + 2h_ae* cosδ₁

d_ae2 = d_e2 + 2h_ae* cosδ₂