
- •Электромагнитный расчет и основные характеристики синхронных машин
- •1. Устройство синхронных машин общего назначения
- •2. Выбор электромагнитных нагрузок и определение главных размеров синхронной машины
- •3. Сердечник и обмотка статора
- •4. Воздушный зазор синхронной явнополюсной машины
- •5. Расчет полюсов ротора и пусковой обмотки
- •6. Расчет магнитной цепи
- •7. Расчет мдс якоря по продольной и поперечной осям
- •8. Расчет параметров обмотки статора
- •9. Расчет мдс обмотки возбуждения при нагрузке
- •10. Расчет обмотки возбуждения
- •11. Потери и кпд
- •12. Основные параметры синхронных машин
- •13. Основные параметры синхронных машин
- •14. Пример расчета трехфазного синхронного двигателя
7. Расчет мдс якоря по продольной и поперечной осям
Известно, что реакция якоря в синхронной машине вызывает изменение магнитного поля, которое должно быть учтено при определении МДС обмотки возбуждения, необходимой при работе машины в режиме нагрузки. При расчете этой МДС используют метод «двух реакций», сущность которого состоит в том, что МДС статора разлагают на две составляющие:
продольную, направленную по оси полюсов, А,
![]() ,
(8.69)
,
(8.69)
и поперечную, направленную по оси, проходящей через середину межполюсного пространства, А,
![]() .
(8.70)
.
(8.70)
В этих
выражениях ![]() - угол сдвига фаз между векторами тока
статора и ЭДС, наведенной результирующим
магнитным потоком по продольной оси
(см. рис. 8.21);
- угол сдвига фаз между векторами тока
статора и ЭДС, наведенной результирующим
магнитным потоком по продольной оси
(см. рис. 8.21); ![]() – МДС обмотки статора (якоря) на пару
полюсов:
– МДС обмотки статора (якоря) на пару
полюсов:
![]() .
(8.71)
.
(8.71)
При рассмотрении вопроса о влиянии реакции якоря на основное поле синхронной машины пользуются понятиями приведенных МДС реакции якоря по продольной оси
![]() (8.72)
(8.72)
и по поперечной оси
![]() .
(8.73)
.
(8.73)
где ![]() – коэффициент приведения МДС реакции
якоря по продольной оси к МДС обмотки
возбуждения и
– коэффициент приведения МДС реакции
якоря по продольной оси к МДС обмотки
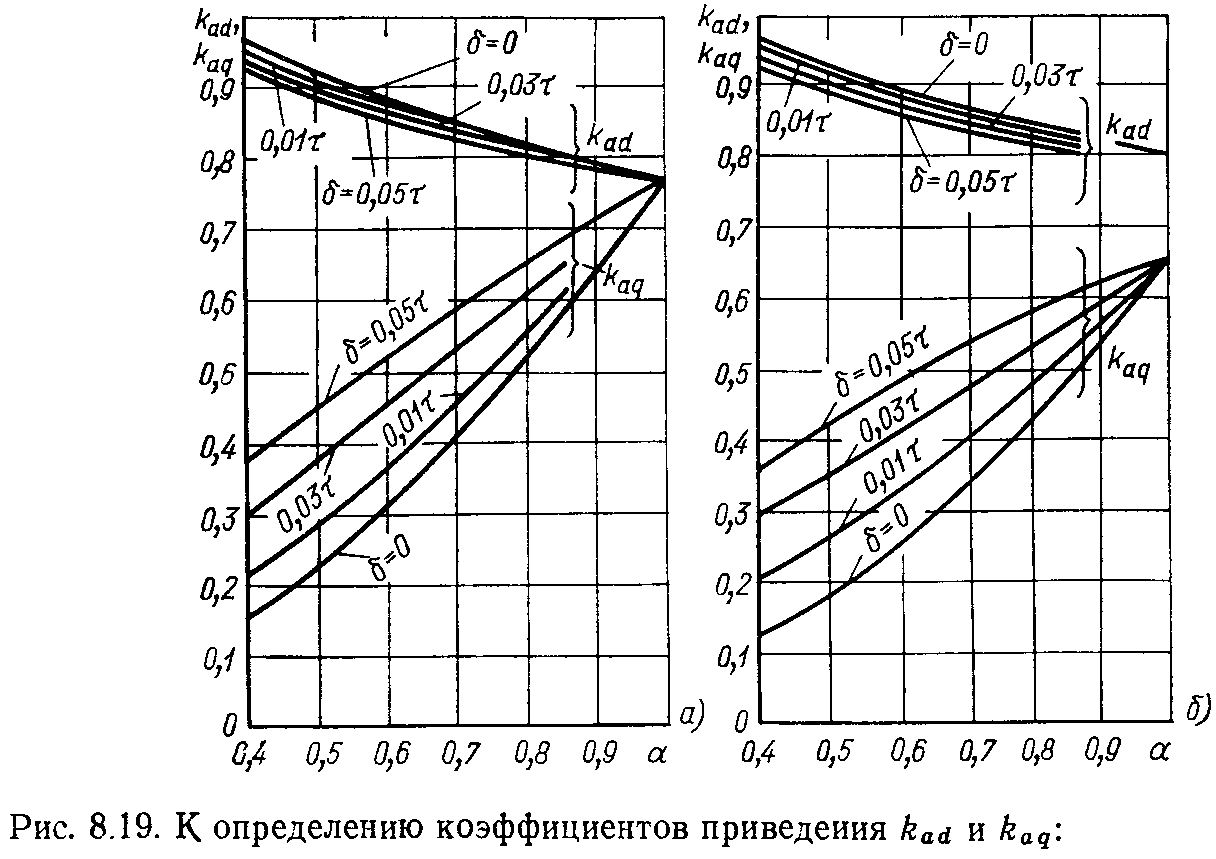
возбуждения и ![]() – коэффициент приведения МДС реакции
якоря по поперечной оси к МДС обмотки
возбуждения. Значения этих коэффициентов
определяют по рис. 8.19.
– коэффициент приведения МДС реакции
якоря по поперечной оси к МДС обмотки
возбуждения. Значения этих коэффициентов
определяют по рис. 8.19.
Е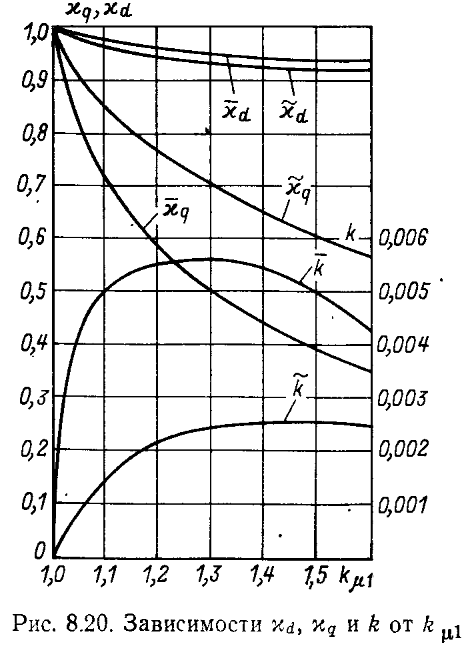 сли
магнитная цепь машины не насыщена, то
продольное и поперечное магнитные поля
не оказывают взаимного влияния, т.е.
действуют независимо. Но обычно магнитные
цепи синхронных машин насыщены и взаимное
влияние продольного и поперечного
магнитных полей в нагруженной машине
необходимо учитывать. Это достигается
умножением МДС
сли
магнитная цепь машины не насыщена, то
продольное и поперечное магнитные поля
не оказывают взаимного влияния, т.е.
действуют независимо. Но обычно магнитные
цепи синхронных машин насыщены и взаимное
влияние продольного и поперечного
магнитных полей в нагруженной машине
необходимо учитывать. Это достигается
умножением МДС ![]() и
и ![]() соотвественно на коэффициенты
соотвественно на коэффициенты ![]() и
и ![]() :
:
![]() ;
;
![]() .
(8.74)
.
(8.74)
Коэффициенты
и
определяют по рис. 8.20 в зависимости от
коэффициента магнитного насыщения
сердечника статора ![]() (8.59), причем коэффициенты
(8.59), причем коэффициенты ![]() и
и ![]() относятся к машинам с равномерным
воздушным зазором (
относятся к машинам с равномерным
воздушным зазором (![]() а коэффициенты
а коэффициенты ![]() и
и ![]() – к машинам с неравномерным зазором
(
– к машинам с неравномерным зазором
(![]()
Поперечная
реакция якоря в машинах с насыщенной
магнитной цепью оказывает размагничивающее
действие, для компенсации которого
необходимо увеличение МДС обмотки
возбуждения на значение ![]() ,
А, равное:
,
А, равное:
при равномерном зазоре
![]() ;
(8.75)
;
(8.75)
при неравномерном зазоре
![]() (8.76)
(8.76)
Значения
коэффициентов ![]() (при равномерном зазоре) и
(при равномерном зазоре) и ![]() (при неравномерном зазоре) определяют
по рис. 8.20.
(при неравномерном зазоре) определяют
по рис. 8.20.
8. Расчет параметров обмотки статора
Статор синхронной машины не отличается от статора асинхронного двигателя. Поэтому для расчета некоторых параметров обмотки статора синхронной машины следует воспользоваться выражениями, приведенными в § 5.4.
Активное сопротивление
фазы обмотки статора, приведенное к
рабочей температуре r1
рассчитывают по (5.67), а его относительное
значение ![]() – по (5.68). При этом расчет средней длины
лобовой части жестких катушек для
высоковольтных машин (6 или 10 кВ) выполняют
по (5.65), а затем увеличивают ее на 40 мм.
– по (5.68). При этом расчет средней длины
лобовой части жестких катушек для
высоковольтных машин (6 или 10 кВ) выполняют
по (5.65), а затем увеличивают ее на 40 мм.
Индуктивное сопротивление рассеяния обмотки статора x1 определяют по (5.79), предварительно определив коэффициент магнитной проводимости дифференциального рассеяния приближенно определяют по формуле
![]() (8.77)
(8.77)
Индуктивное
сопротивление рассеяния фазы обмотки
статора ![]() определяют по (5.80).
определяют по (5.80).
Индуктивное сопротивление взаимной индукции по продольной оси в относительных единицах
![]() ,
(8.78)
,
(8.78)
где ![]() – МДС обмотки статора (якоря), А,
соотвествующая номинальному току
– МДС обмотки статора (якоря), А,
соотвествующая номинальному току ![]() (8.12);
(8.12); ![]() – магнитной напряжение воздушного
зазора при ЭДС
;
– магнитной напряжение воздушного
зазора при ЭДС
;
![]() – коэффициент, учитывающий влияение
магнитных напряжений стали и зазора
между полюсом ротора и статором и зазора
между полюсом и ободом; определяют из
расчета магнитной цепи при магнитном
потоке, соотвествующем ЭДС
– коэффициент, учитывающий влияение
магнитных напряжений стали и зазора
между полюсом ротора и статором и зазора
между полюсом и ободом; определяют из
расчета магнитной цепи при магнитном
потоке, соотвествующем ЭДС ![]() :
:
![]() (8.79)
(8.79)
здесь
![]() – МДС обмотки возбуждения в режиме
холостого хода при ЭДС статора
,
А;
– МДС обмотки возбуждения в режиме
холостого хода при ЭДС статора
,
А; ![]() и
и ![]() – магнитные напряжения воздушного
зазора и стыка между полюсом и ободом
при ЭДС
,
А.
– магнитные напряжения воздушного
зазора и стыка между полюсом и ободом
при ЭДС
,
А.
Индуктивное сопротивление взаимной индукции по поперечной оси в относительных единицах
![]() (8.80)
(8.80)
Синхронное индуктивное сопротивление обмотки статора по продольной оси в относительных единицах
![]() (8.81)
(8.81)
Синхронное индуктивное сопротивление обмотки статора по поперечной оси в относительных
![]() (8.82)
(8.82)
