Теорема о циркуляции вектора

Циркуляция вектора

(

— элемент длины контура, направленный вдоль обхода контура, В₁ = Вcos — составляющая вектора в направлении касательной к контуру (с учетом выбранного направления обхода); — угол между векторами и ).

Теорема о циркуляции вектора

(закон полного тока

для магнитного поля в вакууме)

Циркуляция вектора по произвольному замкнутому контуру равна произведению магнитной постоянной ₀ на алгебраическую сумму токов, охватываемых этим контуром:

г

де п — число проводников с токами, охватываемых контуром L произвольной формы.

Э та теорема справедлива только для поля в вакууме, поскольку для поля в веществе надо учитывать молекулярные токи.

Каждый ток учитывается столько раз, сколько раз он охватывается контуром. Положительным считается ток, направление которого связано с направлением обхода по контуру правилом правого винта; ток противоположного направления считается отрицательным.

М

агнитное поле прямого тока

Расчет произведем на основе теоремы о циркуляции вектора . Замкнутый контур представим в виде окружности радиуса r.В каждой точке этого контура вектор по модулю одинаков и направлен по касательной к окружности

(совпадает с формулой на с. 133).

Поля: потенциальное и вихревое

Циркуляция вектора электростатического поля всегда равна нулю, т. е. электростатическое поле является потенциальным. Циркуляция вектора магнитного поля не равна нулю. Такое поле называется вихревым.

Магнитное поле

соленоида и тороид

Соленоид

Свернутый в спираль изолированный проводник, по которому течет электрический ток.

М агнитное поле соленоида

В

ыберем замкнутый прямоугольный контур ABCDA, как показано на рисунке. Тогда по теореме о циркуляции

(1)

Н

а участках АВ и CD B₁ = 0 и вне соленоида В = 0. Тогда (1) сведется к

(внутри соленоида поле однородно и В₁ = В). Магнитная индукция поля (в вакууме)

Тороид

Кольцевая катушка с витками, намотанными на сердечник, имеющий форму тора, по которой течет ток.

М агнитное поле тороида

И

з опыта известно, что магнитное поле сосредоточено внутри тороида (оно однородно), вне его поле отсутствует.

Линии вектора — окружности с центрами на оси тороида. В качестве контура — окружность радиуса r. По теореме о циркуляции

B = 2r = ₀NI

т. е. магнитная индукция внутри тороида (в вакууме),

(N—число витков тороида).

Поток вектора магнитной индукции.

Теорема Гаусса для поля

Поток вектора магнитной индукции (магнитный поток) сквозь площадку dS

Скалярная физическая величина

где В_п= Bcos — проекция вектора на направление нормали к площадке dS (—угол между векторами и ), - вектор, модуль которого равен dS, а направление совпадает с направлением нормали к площадке.

З нак потока зависит от cos. Поток вектора связывают с контуром, по которому течет ток. А тогда положительное направление нормали определено (оно связывается с током правилом правого винта). Магнитный поток, создаваемый контуром через поверхность, ограниченную им самим, всегда положителен.

Магнитный поток

сквозь произвольную поверхность S

П оле однородно, поверхность плоская и перпендикулярна вектору

Ф_В = BS.

Единица  Вб

1 Вб (вебер) - магнитный поток, проходящий через плоскую поверхность площадью 1 м², расположенную перпендикулярно однородному магнитному полю, индукция которого равна 1 Тл.

1 Вб=1 Тл·м².

Теорема Гаусса для поля

Поток вектора магнитной индукции сквозь произвольную замкнутую поверхность равен нулю:

Э та теорема отражает факт отсутствия магнитных зарядов, вследствие чего линии магнитной индукции не имеют ни начала, ни конца и являются замкнутыми

Работа по перемещению проводника

и контура с током в магнитном поле

Работа по перемещению проводника с током

П

роводник длиной l (он может свободно перемещаться) с током I находится в однородном магнитном поле (см. рисунок). Сила Ампера F = IBI. Под ее действием проводник переместился на dx из положения 1 в 2. Работа, совершаемая магнитным полем,

dA = Fdx = Ibldx = IbdS = IdФ

(учтено, что dS = ldx — площадь, пересекаемая проводником при его перемещении в магнитном поле; BdS = dФ - поток вектора магнитной индукции, пронизывающий эту площадь),

dA = IdФ (1)

Р абота по перемещению проводника с током в магнитном поле равна произведению силы тока на магнитный поток, пересеченный движущимся проводником.

Работа по перемещению контура с током

Р

абота dA сил Ампера при рассматриваемом перемещении контура (см. рисунок) равна сумме работ по перемещению проводников ABC (dA₁) и CDA (dA₂), т. е. dA = dA₁ + dA₂. Согласно (1),

dA₂ = I(dФ₀ + dФ₂)

(dФ₀ - поток, пересекаемый проводником CDА при движении сквозь заштрихованную поверхность, dФ₂ - поток, пронизывающий контур в конечном положении).

dA = - I(dФ₀ + dФ₁)

(знак минус – силы образуют с направлением перемещения тупые углы).

dA = I(dФ₂ - dФ₁).

Р абота по перемещению замкнутого контура с током в магнитном поле равна произведению силы тока в контуре на изменение магнитного потока, сцепленного с контуром.

Глава 15 Электромагнитная индукция

Опыты Фарадея и следствия из них

О

пыт I (рис. а). Если в замкнутый на гальванометр соленоид вдвигать или выдвигать постоянный магнит, то в моменты его вдвигания или выдвигания наблюдается отклонение стрелки гальванометра (возникает индукционный ток); направления отклонения стрелки при вдвигании и выдвигании магнита противоположны. Отклонение стрелки гальванометра тем больше, чем больше скорость движения магнита относительно катушки. При изменении полюсов магнита направление отклонения стрелки изменится. Для получения индукционного тока магнит можно оставлять неподвижным, тогда нужно относительно магнита передвигать соленоид.

О

пыт II. Концы одной из катушек, вставленных одна в другую, присоединяются к гальванометру, а через другую катушку пропускается ток. Отклонение стрелки гальванометра наблюдается в моменты включения или выключения тока, в моменты его увеличения или уменьшения или при перемещении катушек друг относительно друга, (рис. б). Направления отклонений стрелки гальванометра также противоположны при включении и выключении тока, его увеличении и уменьшении, сближении и удалении катушек.

В ыводы

1. Индукционный ток возникает всегда, когда происходит изменение сцепленного с контуром потока магнитной индукции.

2. Сила индукционного тока совершенно не зависит от способа изменения потока магнитной индукции, а определяется лишь скоростью его изменения.

Электромагнитная индукция

Явление, заключающееся в том, что в замкнутом проводящем контуре при изменении потока магнитной индукции, охватываемого этим контуром, возникает электрический ток, получивший название индукционного.

Закон Фарадея (закон электромагнитной индукции)

ЭДС электромагнитной индукции

Обобщая результаты опытов, Фарадей показал, что всякий раз, когда происходит изменение сцепленного с контуром потока магнитной индукции, в контуре возникает индукционный ток; возникновение индукционного тока указывает на наличие в цепи электродвижущей силы, называемой электродвижущей силой электромагнитной индукции.

З акон Фарадея

ЭДС ε_i электромагнитной индукции в контуре численно равна и противоположна по знаку скорости изменения магнитного потока сквозь поверхность, ограниченную этим контуром:

Э тот закон является универсальным: ЭДС ε₁ не зависит от способа изменения магнитного потока.

Вывод закона Фарадея

из закона сохранения энергии

Пусть проводник с током I, помещенный в однородное магнитное поле, перпендикулярное плоскости контура, может свободно перемещаться (см. рисунок на с. 141). Согласно закону сохранения энергии, работа источника тока за время dt складывается из работы на джоулеву теплоту и работы по перемещению проводника в магнитном поле:

где и есть закон Фарадея.

Размерность

.

Правило Ленца. ЭДС индукции

в неподвижных проводниках

В законе Фарадея знак минус показывает, что увеличение потока

вызывает < 0 (поле индукционного тока направлено навстречу потоку); уменьшение потока вызывает > 0 (направления потока и поля индукционного тока совпадают). Знак минус в законе Фарадея - математическое выражение правила Ленца - общего правила для нахождения направления индукционного тока.

П равило Ленца

Индукционный ток в контуре имеет всегда такое направление, что создаваемое им магнитное поле препятствует изменению магнитного потока, вызвавшему этот индукционный ток.

П

ри приближении к замкнутому проводнику

 0

- магнитная индукция поля индукционного тока I_i, причем направление и направление индукционного тока подчиняются правилу правого винта.

ЭДС индукции в неподвижных проводниках

Согласно закону Фарадея, возникновение ЭДС электромагнитной индукции возможно и в случае неподвижного контура, находящегося в переменном магнитном поле. Однако сила Лоренца на неподвижные заряды не действует, поэтому в данном случае ею нельзя объяснить возникновение ЭДС индукции.

Максвелл для объяснения ЭДС индукции в неподвижных проводниках предположил, что всякое переменное магнитное поле возбуждает в окружающем пространстве электрическое поле, которое и является причиной возникновения индукционного тока в проводнике. Циркуляция этого поля по любому неподвижному контуру L проводника представляет собой ЭДС электромагнитной индукции:

Вращение рамки в магнитном поле.

Вихревые токи

Вращение рамки в магнитном поле

Р

амка вращается в однородном магнитном поле (В = const) с угловой скоростью ω = const. Магнитный поток, сцепленный с рамкой площадью S, в любой момент времени t

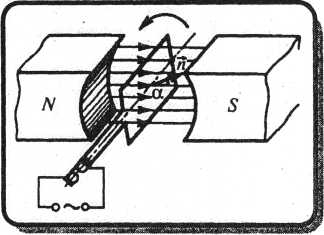
Ф= B_nS = BScos = BS cosωt,

где  = ωt —угол поворота рамки в момент времени t.

При вращении рамки в ней возникает переменная ЭДС индукции:

где ε_max = BSω определяет максимальные значения, достигаемые ε_i. Тогда

ε_i= ε_maxsinωt.

При равномерном вращении рамки в однородном магнитном поле в ней возникает переменная ЭДС, изменяющаяся по гармоническому закону.

В ращение плоской рамки в однородном магнитном поле раскрывает принцип действия генераторов, применяемых для преобразования механической энергии в энергию электрического тока.

Если вращать ряд витков, соединенных последовательно, тем самым увеличивается S. Переменное напряжение снимается с помощью щеток, изображенных на рисунке.

Вихревые токи (токи Фуко)

Индукционный ток возникает и в массивных сплошных проводниках, помещенных в переменное магнитное поле. Эти токи замкнуты в толще проводника и называются вихревыми токами (токами Фуко). Токи Фуко также подчиняются правилу Ленца: их магнитное поле направлено так, чтобы противодействовать изменению магнитного потока, индуцирующего вихревые токи. Например, если между полюсами не включенного электромагнита массивный медный маятник совершает практически незатухающие колебания, то при включении тока он сильно тормозится и быстро останавливается.

Индуктивность контура.

Самоиндукция

Индуктивность контура

Магнитная индукция В поля, создаваемого током, по закону Био-Савара-Лапласа, пропорциональна I. Поэтому сцепленный с контуром магнитный поток

Ф = LI, (1)

где коэффициент пропорциональности L называется индуктивностью контура.

И ндуктивность контура в общем случае зависит только от геометрической формы контура, его размеров и магнитной проницаемости той среды, в которой он находится.

Единица  Гн

1 Гн (генри) - индуктивность такого контура, магнитный поток самоиндукции которого при токе в 1 А равен 1 Вб:

1Гн=1Вб/А=1В·c/А.

Самоиндукция

Возникновение ЭДС индукции в проводящем контуре при изменении в нем силы тока.

П рименяя к самоиндукции закон Фарадея, запишем

Если контур не деформируется и магнитная проницаемость среды не изменяется, то L = const и

где знак минус, обусловленный правилом Ленца, показывает, что наличие индуктивности в контуре приводит к замедлению изменения тока в нем. Так, например, если ток возрастает, ε_s < 0, т. е. ток самоиндукции направлен навстречу току, обусловленному внешним источником, и тормозит его возрастание.

Индуктивность соленоида

Полный магнитный поток сквозь соленоид (потокосцепление)

Подставив эту формулу в (1), получим

(N - число витков соленоида, l - его длина, S - площадь,  -магнитная проницаемость сердечника, ₀ - магнитная постоянная).

Токи при размыкании и замыкании

цепи

Экстратоки самоиндукции

Дополнительные токи за счет возникновения ЭДС самоиндукции при всяком изменении силы тока в цепи. Они направлены противоположно току, создаваемому источником.

Р

азмыкание цепи

В цепи течет постоянный ток I₀ = /R ( - ЭДС источника тока, R - сопротивление). В момент времени t = 0 отключим источник тока, возникает ЭДС самоиндукции, препятствующая уменьшению тока. Ток в цепи определяется законом Ома I = _S/R, или

Разделив переменные и проинтегрировав, получим

I = I₀e^-t/ (1)

где  = L/R - время релаксации. Из (1) следует, что  - время, за которое сила тока уменьшается в е раз.

Из (1) следует, что сила тока при размыкании цепи убывает по экспоненциальному закону (кривая 1 на рисунке).

О ценка ε_S при размыкании цепи

П одставив в (1) I₀ = ε/R, получим

/ . ЭДС самоиндукции

т. е. при резком размыкании контура, содержащего индуктивность, R  R_o, ЭДС самоиндукции _S может во много раз превысить ε. Поэтому контур, содержащий индуктивность, нельзя резко размыкать.

Замыкание цепи

При замыкании цепи наряду с ε возникает ЭДС самоиндукции , ,

препятствующая возрастанию тока. По закону Ома, IR = ε+ε_S, или

Решение этого уравнения

I = I₀ (1-e^-t/) (2)

где I₀ = ε/R - установившийся ток (при t  ∞).

При замыкании цепи нарастание силы тока в цепи задается функцией (2) (кривая 2 на рисунке).

Взаимная индукция

Два контура 1 и 2 с токами I₁ и I₂ расположены близко друг к другу. При протекании в контуре 1 тока I₁ магнитный поток (его поле на рисунке изображено сплошными линиями) пронизывает второй контур:

Ф

₂ = LI₁,

Аналогично

Ф₁ = LI₁

(коэффициенты пропорциональности, называемые взаимной индуктивность контуров, оказались равными).

При изменении силы тока в одном из контуров, в другом индуцируется ЭДС, которая, согласно закону Фарадея,

Взаимная индукция

Явление возникновения ЭДС в одном из контуров при изменении силы тока в другом.

Взаимная индуктивность контуров зависит от геометрической формы, размеров, взаимного расположения контуров и от магнитной проницаемости окружающей контуры среды.

Взаимная индуктивность двух катушек,

намотанных на тороидальный сердечник

М

агнитный поток сквозь один виток второй катушки

Полный магнитный поток (потокосцепление) сквозь N₂ витков вторичной обмотки

Поток  создается током I₁ поэтому

Трансформаторы.

Энергия магнитного поля

Трансформатор

У стройство, применяемое для понижения или повышения напряжения переменного тока.

Р

абота трансформатора основана на явлении взаимной индукции. Переменный ток I₁ создает в первичной обмотке (число витков N₁) переменное магнитное поле, являющееся причиной взаимной индукции во вторичной обмотке (число витков N₂):

Коэффициент трансформации

Отношение N₁/N₂ показывающее, во сколько раз ЭДС во вторичной обмотке трансформатора больше (или меньше), чем в первичной (k >1 — повышающий трансформатор; k < 1 — понижающий).

Э

нергия магнитного поля

Энергия магнитного поля, сцепленного с контуром, Она локализована в пространстве.

Энергия магнитного поля соленоида

В формулу для энергии подставим выражение для получим

Так как I = Bl/(₀N) (с. 139)и B = ₀H, то

г де Sl = V’ – объем соленоида.

Объемная плотность энергии

Магнитное поле соленоида однородно и сосредоточено внутри него, поэтому энергия заключена в объеме соленоида и распределена с объемной плотностью