Вопрос 15 Центральная предельная теорема для независимых одинаково распределенных случайных величин.

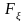Пусть задана последовательность случайных величин , задано некоторое распределение с функцией распределения и  – произвольная сл.величина, имеющая распределение .

Теорема: пусть даны независимые и одинаково распределенные случайные величины. Тогда закон распределения суммы этих случайных величин при n→∞ неограниченно приближенных к нормальному.

х_k – НСВ, m_x – мат.ожидание, 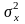- дисперсия

Утверждение: если характерная функция с.в. стремится к характерной функции нормального распределения, то закон распределения самой с.в. стремится к нормальному.

Локальная теорема Муавра-Лапласа: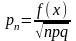

Интегрированная теорема Муавра-Лапласа (является следствием центральной предельной теоремы):

Вопрос 16 Основные понятия математической статистики и т.Д..

Множество случайным образом отобранных объектов называется случайной выборкой. Все множество объектов, из которого производится выборка, называется генеральной совокупностью. Число объектов в выборке называется объемом выборки. Выборки разделяются на повторные (с возвращением) и бесповторные (без возвращения).

Вариационный ряд: пусть для объектов генеральной совокупности определен некоторый признак или числовая характеристика, которую можно замерить. Эта характеристика – случайная величина , принимающая на каждом объекте определенное числовое значение. Из выборки объема n получаем значения этой случайной величины в виде ряда из n чисел: x₁, x₂,..., x_n.(*).

Эти числа называются значениями признака. Если значения признака упорядочить, по возрастанию или убыванию, написав каждое значение лишь один раз, а затем под каждым значением x_i признака написать число m_i, показывающее сколько раз данное значение встречается в ряду (*). то получится таблица, называемая дискретным вариационным рядом. Число m_i называется частотой i-го значения признака.

x1	x2	x3	...	xk
m1	m2	m3	...	mk

Точечные оценки параметров генеральной совокупности: во многих случаях мы располагаем информацией о виде закона распределения случайной величины (нормальный, бернуллиевский, равномерный и т. п.), но не знаем параметров этого распределения, таких как M, D. Для определения этих параметров применяется выборочный метод.

Пусть выборка объема n представлена в виде вариационного ряда. Назовем выборочной средней величину

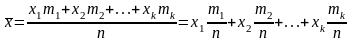
Если значения признака, полученные из выборки не группировать и не представлять в виде вариационного ряда, то для вычисления выборочной средней нужно пользоваться формулой

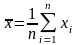
Естественно считать величину выборочной оценкой параметра M. Выборочная оценка параметра, представляющая собой число, называется точечной оценкой.

Выборочную дисперсию можно считать точечной оценкой дисперсии D генеральной совокупности.

Пусть выборочный параметр  рассматривается как выборочная оценка параметра  генеральной совокупности и при этом выполняется равенство M =. Такая выборочная оценка называется несмещенной.

Величина , называется исправленной выборочной дисперсией.

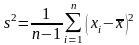
Пусть имеется ряд несмещенных точечных оценок одного и того же параметра генеральной совокупности. Та оценка, которая имеет наимень­шую дисперсию называется эффективной.

Полученная из выборки объема n точечная оценка _n параметра  генеральной совокупности называется состоятельной, если она сходится по вероятности к . Это означает, что для любых положительных чисел  и  найдется такое число n_ , что для всех чисел n, удовлетворяющих неравенству n > n_ выполняется условие .

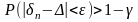и s² являются несмещёнными, состоятельными и эффективными оценками величин M и D.

Вопрос 17 Задача проверки статистических гипотез. Основная и альтернативная, простая и сложная гипотезы. Статистические критерии. Ошибки 1-го и 2-го родов при проверке гипотез. Функция мощности критерия.

Статистической гипотезой называется всякое непротиворечивое множество утверждений {Н₀, Н₁, … , H_k-1} относительно свойств распределения случайной величины. Любое из утверждений H_i называется альтернативой гипотезы. Простейшей гипотезой является двухальтернативная: {H₀, H₁}. В этом случае альтернативу H₀ называют нулевой гипотезой, а H₁ – конкурирующей гипотезой.

Простой гипотезой называют предположение, состоящее в том, что неизвестная функция F(t) отвечает некоторому совершенно конкретному вероятностному распределению

Сложной гипотезой называют предположение о том, что неизвестная функция F(t) принадлежит некоторому множеству распределений, состоящему из более чем одного элемента. 

Критерием называется случайная величина ,где x_i – значения выборки, которая позволяет принять или отклонить нулевую гипотезу H₀. Значения критерия, при которых гипотеза H₀ отвергается, образуют критическую область проверяемой гипотезы, а значения критерия, при которых гипотезу принимают, область принятия гипотезы (область допустимых значений). Критические точки отделяют критическую область от области принятия гипотезы.

Ошибка первого рода состоит в том, что будет отклонена гипотеза H₀, если она верна («пропуск цели»). Вероятность совершить ошибку первого рода обозначается α и называется уровнем значимости. Наиболее часто на практике принимают, что α = 0,05 или α = 0,01.

Ошибка второго рода заключается в том, что гипотеза H₀ принимается, если она неверна («ложное срабатывание»). Вероятность ошибки этого рода обозначается β. Вероятность не допустить ошибку второго рода (1-β) называют мощностью критерия. Для нахождения мощности критерия необходимо знать плотность вероятности критерия при альтернативной гипотезе. Простые критерии с заданным уровнем значимости контролируют лишь ошибки первого рода и не учитывают мощность критерия.

Обе эти характеристики вычисляются с помощью функции мощности критерия. В частности, вероятность ошибки первого рода есть функция мощности, вычисленная при нулевой гипотезе.

Функция мощности статистического критерия определяется, как вероятность отвергнуть нулевую гипотезу при заданном распределении наблюдений. Функция мощности является функцией от распределения наблюдаемых случайных величин.