Вопрос 11 Случайные величины, функции распределения, их свойства. Абсолютно непрерывные и дискретные распределения. Типовые распределения: биномиальное, пуассоновское, нормальное.

Случайной величиной x называется величина, значение которой х_i (i=1÷n) известны, но какое из них примет случайная величина – неизвестно. Переменная величина х, принимаемая в результате испытания одно из конечных значений или бесконечных последовательностей значений, называется дискретной случайно величиной если каждому х_i соответствует определенная вероятность р_i того, что х примет значение х_i. Функциональная зависимость р_i от х_i называется (ряд) закон распределения:

x=(x₁,x₂,…,x_n)

xi	x1	x2	…	xn
pi	p1	p2	…	pn

То, что случайная величина х принимает одно из значений последовательности x₁… x_n, есть событие достоверное, потому должно выполняться условие:

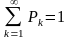
Непрерывная случайная величина х – величина, которая может принимать любые значения из некоторого интервала (a;b) возможных ее значений.

Закон распределения может быть задан не только аналитически: p_k=f(x_k), но и графически в виде многоугольника распределений вероятностей: строят точки с координатами (p_i;x_i) и соединяют их ломаной.

Функция f(x) называется функцией распределения случайной величины х, если в каждой точки х определена вероятность события {x<x_i}.

Свойства: 1 0<f(x)<1; 2 f(x) – монотонно возрастает; 3 f(x₁)<f(x₂), x₁<x₂; 4 f(–∞)=0, f(∞)=1, lim f(A),A→∞.

х – дискретная случайная величина; x=(x₁,…,x_n); f(x)=P(x<x_i), где i=1÷n

х – непрерывная случайная величина; x=(a;b); f(x)=P(x<x), где x€(a;b)

В общем виде: ,

Характеристики случайных величин:

х – дискретная случайная величина

Биномиальное распределение имеет дискретная случайная величина х, если она принимает значения 0,1,…,m,..,n со следующими вероятностями:

P_n(m)=P_n(X=m)=C_n^m p^m q^n-, где 0<p<1; q=1-p; m=0, 1,2,...,n.

Числовые характеристики биномиального распределения:

M_x =np, D_x =npq

Условия возникновения: проводится n одинаковых независимых, в каждом из которых событие А появляется с вероятностью р. Случайная величина х – число опытов, в которых произошло событие А

Распределение Пуассона имеет дискретная случайная величина х, если она принимает значения 0,1,…,∞ со следующими вероятностями:

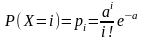
Закон Пуассона зависит от одного параметра : он является одновременно M_X и D_X случайной величины х, распределённой по закону Пуассона.

Условия возникновения:

1 распределение Пуассона является предельным случаем биномиального, когда число опытов n неограниченно увеличивается, а вероятность p события A в одном опыте стремится к 0, так что существует предел: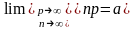

2 случайная величина х – число событий пуассоновского потока поступивших в течение интервала τ, причем параметр а=τλ, где λ – интенсивность потока.

Говорят, что случайная величина х распределена по нормальному закону (закону Гаусса) с параметрами m, , если

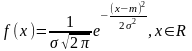
Условия возникновения: нормальное распределение возникает в тех случаях, когда складывается много независимых (либо слабо зависимых) случайных величин х₁,х₂,...,х_п