Вопрос 10 Вероятностное пространство. Аксиомы теории вероятностей. Классическое определение вероятности.

Случайная величина – это событие, которое при осуществлении некоторых условий может произойти или не произойти, т.е. событием можно назвать любой исход опыта. Оно может быть: достоверным – если оно обязательно произойдет в результате опыта; невозможным – если в результате опыта оно произойти не сможет.

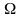- множество элементарных событий, 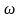- элемент события, 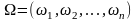- пространство событий.

Вероятность появления события – частота. Относительной частотой события А называют отношение числа m проявления данного события к числу n проведенных испытаний:

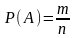, n – число всех исходов опыта, m – число благоприятных событий

При неограниченном увеличении числа опытов событие А сводится к вероятности появления этого события:

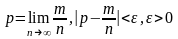
События могут быть совместными (происходят одновременно) или случайными (происходят в разное время). Случайные события образуют полную группу, если при каждом испытании может произойти любое из них и не может появиться какое-либо иное событие, несовместимое с ними. События такой группы называются благоприятствующими появлению события А, если появление этого случая влечет за собой появление события А.

Вероятностью события А называется отношение числа m благоприятствующих случаев к числу всех возможных случаев n, образующих полную группу равновозможных несовместимых событий: 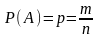. Из определения вероятности следует, что оно удовлетворяет соотношению: .

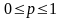Если какому-либо событию благоприятствуют все n случаев, образующих полную группу равновозможных событий, то такое событие называется достоверным (р=1); событие, которому не благоприятствует ни один из n случаев, образующих полную группу равновозможных событий, называется невозможным (р=0).

Суммой двух событий А и В называется событие С, состоящее в появлении хотя бы одного из этих событий: А+В=С (либо А, либо В).

Теорема сложения: пусть при данном испытании могут иметь место события А с Р(А) и событие В с Р(В), причем А и В – несовместные, тогда Р(А+В)=Р(А)+Р(В).

Два события называются противоположными, если они не совместимы и образуют полную группу. Пусть вероятность появления А есть p, а вероятность появления В – q, следовательно, на основании теоремы сложения: сумма вероятностей противоположных событий равна 1: p+q=1, т.е. q=1-p, p=1-q.

Следствие: если случайные события А₁,А₂,...,А_n образуют полную группу несовместимых событий, то. Р(А₁)+ Р(А₂)+…+ Р(А_n)=1.

Случайные события А и В называются совместимыми если при данном испытании могут произойти оба эти события, т.е. произойдет совмещение А и В.

Теорема: вероятность суммы совместимых событий вычисляется как: Р(А+В)=Р(А)+Р(В)–Р(АВ):

Событие А называется независимым от события В если вероятность появления события А не зависит от того, произошло событие В или нет.

Теорема умножения: Если случайные события А и В независимы, то вероятность совместных событий А и В равна произведению вероятностей появления событий А и В: Р(АВ)=Р(А)Р(В).

Событие А называется зависимым от события В если вероятность появления события А зависит от того, произошло или не произошло событие В.

Вероятность того, что произошло событие А при условии, что произошло событие В называется условной вероятностью события А при условии В: Р(А/В).

Теорема: вероятность совмещения 2 событий равняется произведению вероятности одного на условную вероятность второго, вычисленную при условии, что 1 событие произошло: Р(АВ)=Р(В)Р(А/В)=Р(А)Р(В/А). ,

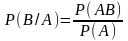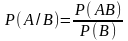
Теорема: пусть событие А может произойти лишь с одним из событий Н, образуя полную группу, тогда А можно вычислить, как: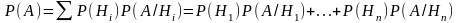 .