Вопрос 8 Евклидово (унитарное) пространство и его свойства. Ортогонализация системы векторов. Существование ортонормированного базиса. Ортогональное дополнение подпространства.

Евклидово пространство (Е) – линейное векторное пространство с определенным скалярным произведением.

||а|| – норма (n-мерный вектор),

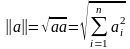
Линейное пространство R называется евклидовым, если имеется правило, которое позволит для каждых двух векторов x и y из R построить действительное число, называемое скалярным произведением векторов x и y и обозначаемое (x,y), причем это правило удовлетворяет следующим условиям:

1 (x,y)=(y,x); 2 (x,y+z)=(x,y)+(x,z); 3 (ax,y)=a(x,y), для любого действительного числа a; 4 (x,x)>0, если x  0.

Из этих условий следует, что: 1 (y+z,x)=(y,x)+(z,x); 2 (x,ay)=a(x,y); 3 (0,x)=0 для любого вектора x.

Скалярное произведение любого вектора xR на себя называется скалярным квадратом вектора x.

Длиной вектора x в евклидовом пространстве называется квадратный корень из скалярного квадрата этого вектора.

Если a – любое действительное число, а x – любой вектор евклидова пространства, то |ax|=|a| |x|.

Вектор, длина которого равна единице, называется нормированным. Если xR – ненулевой вектор, то нетрудно видеть, что (1/|x|) является нормированным вектором. Если x,y – ненулевые векторы, а угол между ними равен /2, то (x,y)=0 тогда говорят, что векторы x и y ортогональны и пишут xy.

Неравенство Каши-Буняковского: модуль скалярного произведения векторов не превосходит их норм.

Базис e₁,e₂,…,e_n евклидова пространства называется ортогональным, если (e_i,e_k)=0 при i  k.

Теорема: во всяком евклидовом пространстве имеется ортогональный базис.

Система векторов называется ортогональной, если: 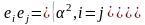. Если α=1, тогда система ортонормированная.

Если ортогональный базис состоит из нормированных векторов, то этот базис называется ортонормированным.

Если в n-мерном евклидовом пространстве известен какой-нибудь базис f₁,f₂,…,f_n, то в этом пространстве всегда можно найти и ортонормированный базис e₁,e₂,…,e_n.

Базис называется ортонормированным, если его векторы попарно ортогональны и по длине равны 1.

Теорема: если базис ортонормированный, то скалярное произведение векторов выражается через их компоненты по формуле:

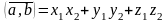
Теорема позволяет написать выражение длины вектора через его компоненты в ортонормированном базисе:

Вопрос 9 Кольца вычетов. Малая теорема Ферма. Сравнения первой степени. Китайская теорема об остатках.

Кольцо – множество с операциями, если: 1. группа по первой операции, т.е.: выполняется свойство ассоциативности: a+(b+c)=(a+b)+c. существует нейтральный элемент: a+0=a, существует обратный элемент: a+(–a)=a 2. выполняется свойство дистрибутивности: (a+b)c=ac+bc; c(a+b) =ca+cb

Вычет целого числа b по модулю m>0 – такое целое число a, что разность a–b делится на m, т.е. имеет место сравнение ba(mod m). Так 24 есть вычет числа 3 по модулю 7.

Если вместо чисел брать элементы кольца, то говорят о кольцах вычетов.

Пусть mN, тогда для любого целого числа aZ однозначно определен остаток от деления a на m, то есть a представимо в виде a=mq+r.

Два целых числа называются сравнимыми по модулю m, если a–b делится на m: ab(mod m).

Сравнимость чисел a и b по модулю m равносильна: равенству остатков от деления a и b на m.

Отношение сравнимости по произвольному модулю m есть отношение эквивалентности на множестве целых чисел. Это отношение эквивалентности индуцирует разбиение множества целых чисел на классы эквивалентных между собой элементов, т.е. в один класс объединяются числа, дающие при делении на m одинаковые остатки. Число классов эквивалентности в точности равно m.

Теорема Ферма: для простого числа p и любого целого числа n справедливо сравнение n^p n(mod p); пусть р – простое число, и а не делится на р, тогда: а^p-1 1(mod p).

Китайская теорема об остатках: для любых взаимно простых положительных n и m и для любых целых чисел a и b существует такое целое число x, что справедливы сравнения xa(mod n) и xb(mod m).

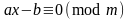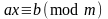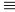(1) – сравнение первой степени, (2). Два сравнения называются равносильными, если их решения совпадают. За одно решение сравнения будем принимать целый класс чисел, сравнимых с данным решением по модулю m. Теорема: Пусть (a, m) = d. Сравнение ах b (mod т) невозможно, если b не делится на d. При b, кратном d, сравнение имеет d решений.