
- •Вопрос 1 Непрерывность действительных функций одного и многих действительных переменных. Свойства непрерывных функций.
- •Вопрос 2 Числовой ряд. Сходящиеся ряды и их простейшие свойства. Функциональные ряды. Равномерно сходящиеся ряды. Степенные ряды. Область и радиус сходимости степенного ряда.
- •Вопрос 4 Матрицы над кольцом и операции над ними. Определители матриц и их свойства. Ранг матрицы над полем. Обратная матрица и способы ее вычисления.
- •Вопрос 5 Векторные пространства над полем. Линейно зависимые и независимые системы векторов. Подпространства векторного пространства, операции над ними. Свойства конечномерных векторных пространств.
- •Вопрос 6 Кольцо многочленов над кольцом с единицей. Делимость многочленов с остатком. Значение многочлена, его корень.
- •Вопрос 8 Евклидово (унитарное) пространство и его свойства. Ортогонализация системы векторов. Существование ортонормированного базиса. Ортогональное дополнение подпространства.
- •Вопрос 9 Кольца вычетов. Малая теорема Ферма. Сравнения первой степени. Китайская теорема об остатках.
- •Вопрос 10 Вероятностное пространство. Аксиомы теории вероятностей. Классическое определение вероятности.
- •Вопрос 11 Случайные величины, функции распределения, их свойства. Абсолютно непрерывные и дискретные распределения. Типовые распределения: биномиальное, пуассоновское, нормальное.
- •Вопрос 12 Условные вероятности. Независимость событий. Формула полной вероятности. Формулы Байеса. Независимые случайные величины.
- •Вопрос 13 Математическое ожидание случайной величины и его свойства. Примеры. Дисперсия случайной величины и ее свойства. Вычисление математических ожиданий и дисперсий типовых распределений.
- •Вопрос 15 Центральная предельная теорема для независимых одинаково распределенных случайных величин.
- •Вопрос 16 Основные понятия математической статистики и т.Д..
- •Вопрос 18 Критерии согласия. Критерий согласия Пирсона (критерий 2).
- •Вопрос 19 Алгоритмы сортировки. Сортировки сравнениями: пузырьковая сортировка и сортировка вставками. Оценки трудоемкости.
- •Вопрос 21 Цифровая сортировка как пример сортировки подсчетом. Бинарный и интерполяционный поиск. Оценки трудоемкости.
- •Вопрос 22 Алгоритмы поиска в деревьях. Деревья двоичного поиска. Алгоритм вставки и удаления элемента в дерево двоичного поиска. Оценки трудоемкости.
- •Вопрос 24 Теорема Шеннона для канала без шума и ее практическое значение.
- •Вопрос 25. Теорема Шеннона для канала с шумом и ее практическое значение.
- •Вопрос 26 Классификация помехоустойчивых кодов и принципы их построения.
- •Вопрос 27 Угрозы безопасности информации. Классификация и модель угроз безопасности. Угрозы конфиденциальности, целостности, доступности, раскрытия параметров ас.
- •Вопрос 28 Понятие политики безопасности. Формирование и структура политики иб. Дискреционная политика безопасности. Мандатная политика безопасности.
- •Вопрос 29 Основные положения руководящих документов фстэк в области зи.
- •Вопрос 30 Определение и классификация нарушителя. Модель нарушителя. Модель нарушителя в соответствии с рд фстэк.
- •Вопрос 32 Стандарт по обеспечению информационной безопасности гост р исо/мэк 17799. Практические правила управления иб. Отправная точка для внедрения иб.
- •Вопрос 33 Стандарт по обеспечению информационной безопасности гост р исо/мэк 27001. Система менеджмента информационной безопасности.
- •Вопрос 34 Формальные модели безопасности. Модель Белла-Лападула как основа построения систем мандатного разграничения доступа. Основные положения модели.
- •Вопрос 35 Методы и средства ограничения и управления доступом. Пас управления доступом. Типовая структура и типовые функции пас управления доступом.
- •Вопрос 36 Методы и средства привязки программного обеспечения к аппаратному окружению и физическим носителям.
- •Вопрос 37. Защита программ от исследования. Методы и средства защиты.
- •Вопрос 38. Защита от разрушающих программных воздействий (рпв). Методы и средства защиты от разрушающих программных воздействий. Изолированная программная среда.
- •Вопрос 39 Информативные сигналы и их источники. Побочные электромагнитные излучения и наводки. Структура, классификация и основные характеристики технических каналов утечки информации.
- •Вопрос 40 Скрытие речевой информации в каналах связи. Энергетическое скрытие акустических информативных сигналов.
- •Вопрос 42 Криптосистемы с открытым ключом. Понятие сертификата. Криптосистема rsa. Выбор параметров.
- •Вопрос 43 Криптографические хэш-функции. Стандарт гост р 34.11.
- •8.3 Этап
- •Вопрос 44 Цифровая подпись. Схемы цифровой подписи. Стандарт гост р 34.10.
- •45 Блочные шифры. Режимы блочных шифров. Гост 28147.
- •46 Протоколы открытого ключевого обмена. Диффи-Хеллман
- •Вопрос 47. Классификация ключей по типам алгоритмов, их функциям, уровням и криптопериоду.
- •Вопрос 48 Основные механизмы безопасности операционных систем (ос): средства и методы аутентификации в ос, модели разграничения доступа, организация и использование средств протоколирования.
- •Вопрос 49. Администрирование ос: основные задачи и принципы сопровождения системного по, управления безопасности ос.
- •Вопрос 50 Классификация сетевых атак. Классификация средств сетевой защиты
- •Вопрос 51. Основные принципы обеспечения безопасности в Internet.
- •Вопрос 53 Защита информации ограниченного доступа: коммерческой тайны.
- •Вопрос 54 Защита государственной тайны.
- •Вопрос 55 Защита информации ограниченного доступа: персональных данных.
- •Вопрос 56 Лицензирование деятельности в области защиты информации.
- •Вопрос 57. Сертификация средств защиты информации.
- •Вопрос 58. Аттестация объектов информатизации.
Вопрос 6 Кольцо многочленов над кольцом с единицей. Делимость многочленов с остатком. Значение многочлена, его корень.
п
—
целое положительное число,
 ,
где а0
,a1,…,an
—
комплексные числа.
,
где а0
,a1,…,an
—
комплексные числа.
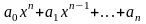 и называется многочленом n-й
степени от неизвестного х.
Пусть
Р
—
некоторое числовое поле. Элементы поля
Р
мы
будем обозначать начальными буквами
а,
b,
с, ... латинского
алфавита. Многочленом
от х над полем Р мы назовем выражение
вида:
и называется многочленом n-й
степени от неизвестного х.
Пусть
Р
—
некоторое числовое поле. Элементы поля
Р
мы
будем обозначать начальными буквами
а,
b,
с, ... латинского
алфавита. Многочленом
от х над полем Р мы назовем выражение
вида:
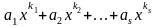 ,
,
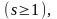 , где а1
,a2,…,as
— числа
из Р, k1
<
k2
<
... < ks
—
целые
неотрицательные числа.
Р[х] это
множество многочленов. Действия сложения
и умножения подчиняются основным
алгебраическим законам. Множество
многочленов Р
[х] называют
кольцом
многочленов от х над Р.
Степень
многочлена
наибольшую из степеней его членов, у
которых коэффициенты не равны нулю.
Теорема 1.
Для
любых двух многочленов f(x)
и g(x)
можно найти такие многочлены q(x)
и r(х),
что f(x)=g(x)q(x)
+ r(x),
причем
степень r(х)
меньше степени g(x)
или же r(x)
= 0. Многочлены q
(х) и r(х),
удовлетворяющие этому условию,
определяются однозначно. Делимость
многочленов –
это способность одного многочлена
делиться на другое.
Многочлен
q(х)
называется
частным
от деления
f(x)
на
g(x),
а
r(x)—
остатком
от
этого деления. Свойства
делимости многочленов.
Если в (1)
, где а1
,a2,…,as
— числа
из Р, k1
<
k2
<
... < ks
—
целые
неотрицательные числа.
Р[х] это
множество многочленов. Действия сложения
и умножения подчиняются основным
алгебраическим законам. Множество
многочленов Р
[х] называют
кольцом
многочленов от х над Р.
Степень
многочлена
наибольшую из степеней его членов, у
которых коэффициенты не равны нулю.
Теорема 1.
Для
любых двух многочленов f(x)
и g(x)
можно найти такие многочлены q(x)
и r(х),
что f(x)=g(x)q(x)
+ r(x),
причем
степень r(х)
меньше степени g(x)
или же r(x)
= 0. Многочлены q
(х) и r(х),
удовлетворяющие этому условию,
определяются однозначно. Делимость
многочленов –
это способность одного многочлена
делиться на другое.
Многочлен
q(х)
называется
частным
от деления
f(x)
на
g(x),
а
r(x)—
остатком
от
этого деления. Свойства
делимости многочленов.
Если в (1)
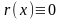 ,
то f(x)
делится на g(x).
1)
,
то f(x)
делится на g(x).
1)
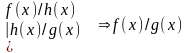 ;
2)
;
2)
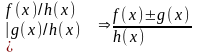 ;
3)
;
3)
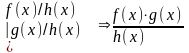 ;
4)
;
4)
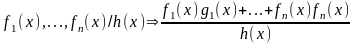 ;
5)
;
5)
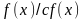 ;
6)
;
6)
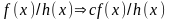 ;
7)
многочлены q(x)
и f(x)
делятся друг на друга тогда и только,
когда они имеют одну и ту же степень; 8)
многочлен f(x)
любой степени всегда делится на любой
многочлен нулевой степени.
;
7)
многочлены q(x)
и f(x)
делятся друг на друга тогда и только,
когда они имеют одну и ту же степень; 8)
многочлен f(x)
любой степени всегда делится на любой
многочлен нулевой степени.
Пусть
даны ненулевые многочлены f(x)
и
g(х).
Если остаток от деления f(x)
на
g(х)
равен
нулю, то
многочлен g(х)
называется
делителем
многочлена
f(x).
Многочлен g(х)
тогда и только тогда будет делителем
многочлена f(x),
если существует многочлен ψ(x),
удовлетворяющий равенству
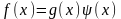
Если f(x) = a0xn+ a1xn-1 + ... +an (1) есть некоторый многочлен, а с — некоторое число, то число f(c) = a0 cn+ a1 cn-1 + ... +an, полученное заменой в выражении (1) для f(x) неизвестного x числом с и последующим выполнением всех указанных операций, называется значением многочлена f(x) при х = с. Если f(с)=0, т. е. многочлен f(x) обращается в нуль при подстановке в него числа с вместо неизвестного, то с называется корнем многочлена f(x).
Теорема Безу: Значение многочлена f(x) в некоторой точке с совпадает с остатком от деления этого многочлена на линейный двучлен (х-с). Следствие: Если некоторое число с является корнем f(x), то f(x) делится на цело на линейный двучлен (х-с).
Вопрос 7 Наибольший общий делитель (НОД) и наименьшее общее кратное (НОК) многочленов над полем. Свойства НОД и алгоритм его нахождения. Взаимно простые многочлены и их свойства. Неприводимые многочлены и их свойства. Каноническое разложение многочлена и его однозначность.
Число dZ, делящее одновременно числа а,b,c,...,kZ , называется общим делителем этих чисел. Наибольшее d с таким свойством называется наибольшим общим делителем: d=(a,b,c,...,k).
Для многочленов также имеет место наибольший общий делитель. Только вместо чисел берутся многочлены.
Наименьшее общее кратное для нескольких чисел – наименьшее, делящееся на каждое из них.
Свойства НОД.
1 если (a,b)=d, то найдутся такие целые числа u и v , что d=au+bv;
2 для любых целых чисел а и k, справедливо: (а,kа)=а; (1,а)=1.
3 если a=bq+c , то совокупность общих делителей a и b совпадает с совокупностью общих делителей b и с , в частности, (a,b)=(b,c);
4 пусть a,b и m – произвольные целые числа, тогда (am,bm)=m(a,b).
Многочлены a и b называются взаимно простыми, если (a,b)=1.
Пусть даны ненулевые многочлены f(x) и g(х). Если остаток от деления f(x) на g(х) равен нулю, т. е., как говорят, f(x) делится на g(х), то многочлен g(х) называется делителем многочлена f(x). Пусть даны произвольные многочлены f(x) и e(x). Многочлен g(x) будет называться общим делителем для f(x) и g(x), если он служит делителем для каждого из многочленов. Если других общих делителей эти два многочленa не имеют, то они называются взаимно простыми. В общем же случае многочлены f(x) и g(x) могут обладать делителями, зависящими от х.
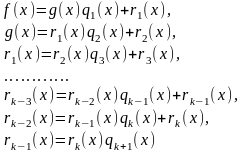 алгоритм Евклида –
нахождение НОД
алгоритм Евклида –
нахождение НОД
Если некоторый многочлен в степени >0 раскладывается на произведение 2-х других многочленов с коэффициентами из того же поля, что и исходный многочлен, причем степени этих многочленов >0 и меньше степени исходного многочлена, то такой многочлен называется приводимым над полем чисел, в противном случае многочлен неприводимый. Многочлен нулевой степени нельзя считать приводимым, а также нельзя считать неприводимым многочленом. Основная теорема теории делимости многочленов. Любой многочлен выше 0-й степени над полем Р единственным образом представляется в виде произведения: Р(x) = p1(x) р2(х) ... pk(x). Свойства неприводимых многочленов. 1) если p1(x) и p2(x) — неприводимые многочлены над полем Р и p1(x) делится на p2(х), то справедливо p1(x)=cp2(x), где c≠0; 2) многочлен f (х) из Р[х] тогда и только тогда не делится на многочлен р(х), неприводимый над полем Р, когда f(x) и р(х) взаимно просты; 3) если произведение f(x) g(х) двух многочленов f(х) и g(x) из Р[х] делится на многочлен р(х), неприводимый над Р, то на р(х) делится по меньшей мере один из сомножителей f(x), g(x). Теорема 1. Над полем всех комплексных чисел неприводимыми являются только полиномы первой степени.
Теорема о приводимости. Если многочлен с целыми коэффициентами f(x) является приводимым над полем Q, тогда он раскладывается в произведение многочленов с целыми коэффициентами f(x)=f1(x)*f2(x) (1).
