Вопрос 26 Классификация помехоустойчивых кодов и принципы их построения.

Принципы построения помехоустойчивых кодов. Кодирование с помощью которого можно устранять ошибки обусловленные наличием шума в канале называется помехоустойчивым. Коды способные исправлять и обнаруживать ошибки называется помехоустойчивым кодом.

Эти коды строятся таким образом, что для передачи сообщения используется лишь часть кодовых слов, которые отличаются друг от друга более чем в одном символе. Эти кодовые слова называются разрешенными. Все остальные кодовые слова не используются и относятся к числу запрещенных.

Рассмотрим основополагающие принципы, заложенные в основу построения помехоустойчивых кодов. Непременным свойством помехоустойчивых кодов является наличие избыточности. При этом необходима не просто любая избыточность, а специфическая, определяемая свойствами канала и правилом построения кода. И позволяющая с минимальными затратами повысить вероятность передачи.

Сначала с помощью эффективного кодирования до минимума уменьшают избыточность источника сообщений, а затем в процессе помехоустойчивого кодирования вносят в передаваемый сигнал избыточность, позволяющую простыми средствами поднять верность. При использовании помехоустойчивого кода возможно декодирование с обнаружением и исправлением ошибок.

О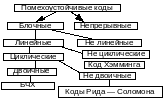 сновная классификация помехоустойчивых кодов. В непрерывных кодах  передаваемая информационная последовательность не разделяет кодовые комбинации. Избыточные элементы размещаются в определенном порядке между информационными. В блочных кодах передаваемая информационная последовательность разбивается на отдельные кодовые комбинации, которые кодируются и декодируются независимо друг от друга.

Блочные делятся на линейные и нелинейные. Линейными кодами называются блочные разделимые (n,k)-коды, в которых проверочные элементы представляют собой линейные комбинации информационных, несистематические коды таким свойством не обладают.

Линейные делятся на циклические и не циклические.

Код называют циклическим, если для любого кодового слова циклическая перестановка символов также дает кодовое слово. К не циклическим относится код Хэмминга

Циклические делятся на двоичные и не двоичные. Способы задания линейных кодов 1) Перечислением кодовых слов, т.е. составление списка всех кодовых слов кода 2) Системой проверочных уравнений и табличных коэффициентов, 3) Матричный, основан на построении порождающей и проверочной матриц

Основные свойства линейных кодов. 1) Произведение любого кодового слова 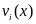на транспонированную проверочную матрицу дает нулевой вектор размерности n-k

2) Произведения кодового слова 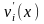с ошибкой (неразрешенная комбинация) на транспонированную проверочную матрицу называется синдромом и обозначается S_i(x) 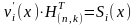3) Между порождающей и проверочной матрицами в систематическом виде существуют однозначные соответствия 4) Произведение информационного слова на порождающую матрицу дает кодовое слово кода: 6) Кодовое расстояние любого (n,k) кода удовлетворяет 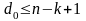- граница Сингтона. Линейный (n,k) код, удовлетворяющий этому неравенству, называется кодом с максимальным расстоянием.

Код Хэмминга – класс блочных кодов, который имеет следующую структуру: 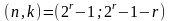. Минимальное кодовое расстояние d₀=3, поэтому они способны исправлять все одиночные ошибки или обнаруживать все ошибочные комбинации из двух или менее ошибок в блоке. Код Хэмминга является классом для которого выражение, определяющее границу Хэмминга имеет место.

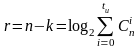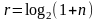
. Подставляя в последнее равенство t_и=1, т.к. код Хэмминга исправляет лишь одиночные ошибки, получаем: 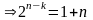. Т.о., коды Хэмминга имеют наименьшее возможное при заданной длине кодирование комбинации n, количество проверочных разрядов r, которое обеспечивает минимальное кодовое расстояние d₀=3.

Проверочная матрица кода Хэмминга имеет r строк и 2^r-1 столбцов, причем столбцами являются все различные не нулевые последовательности.

Циклическим кодом называется минимальный блочный (n, k) код, обладающий свойством цикличности, которое заключается в следующем: циклический сдвиг влево на один разряд любого разрешенного слова дает также разрешенное слово. Множество кодовых слов циклического слова может быть представлено совокупностью многочленов степени (n-1) и делящихся на некоторый многочлен g(x) степени r=n-k, являющихся сомножителями двучлена xn+1.

Матричное задание кодов. Циклический код может быть задан порождающей и проверочной матрицами. Для их построения достаточно знать многочлены g(x) и h(x). Одна из основных задач, выбор порождающего многочлена g(x) для построения циклического кода, обеспечивающего требуемое минимальное кодовое расстояние для гарантируемого обнаружения и исправления t-кратных ошибок.

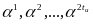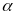Коды БЧХ Важным классом циклических кодов, способных исправлять многократные ошибки, являются коды БЧХ. Примитивным кодом БЧХ, исправляющим tu ошибок, называется код длиной n=qm-1 над полем GF(g), для которого элементы являются корнями порождающего многочлена. – примитивный элемент поля GF(qm). Число проверочных элементов кода БЧХ удовлетворяет соотношению: r=n–k=mtи.

Код Рида - Соломона - недвоичные циклические коды, позволяющие исправлять ошибки в блоках данных. Элементами кодового вектора являются не биты, а группы битов (блоки). Является частным случаем БЧХ-кода.