Вопрос 21 Цифровая сортировка как пример сортировки подсчетом. Бинарный и интерполяционный поиск. Оценки трудоемкости.

Цифровая сортировка. Этой сортировкой можно сортировать целые неотрицательные числа большого диапазона. Идея состоит в следующем: отсортировать числа по младшему разряду, потом устойчивой сортировкой сортируем по второму, третьему, и так до старшего разряда. В качестве устойчивой сортировки можно выбрать сортировку подсчетом, в виду малого времени работы.

Так как сортировка подсчетом вызывается константное число раз, то время работы всей сортировки есть O(n). Таким способом можно сортировать не только числа, но и строки, если же использовать сортировку слиянием в качестве устойчивой, то можно сортировать объекты по нескольким полям.

Бинарный поиск в упорядоченном массиве: алгоритм предполагает деление упорядоченного списка ключей пополам до тех пор, пока в результате очередного деления число элементов в отрезке файла не уменьшится до одного. В этом случае уже можно сказать, был поиск удачным или нет. Алгоритм имеет сложность log N. Лучших результатов не может дать ни один метод, основанный на сравнении ключей, появляющихся с равной вероятностью. Однако, метод предназначен только для поиска, как и все методы, основанные на структуре исходного файла в виде последовательного списка. При включении новых ключей очевидны большие затраты по пересылке элементов

Интерполяционный поиск: алгоритм интерполяционного поиска предполагает, что исходный файл упорядочен по величинам ключей поиска. Идея алгоритма состоит в том, что делается предположение о равномерном распределении величин в некотором их диапазоне от u до l. Поэтому, зная величину х ключа поиска, можно предсказать более точное положение искомой записи, чем просто в середине некоторого отрезка файла. Формула нахождения положения следующего элемента для сравнения следует из деления длины отрезка u-l пропорционально величинам разностей ключей K[u]-K[l] и X-K[l]. Интерполяционный поиск ассимптотически предпочтительнее бинарного, если только соблюдается гипотеза о равномерном распределении величин ключей. Интерполяционный поиск работает за log(logN) операций, если данные распределены равномерно. Как правило, он используется лишь на очень больших таблицах, причем делается несколько шагов интерполяционного поиска, а затем на малом подмассиве используется бинарный или последовательный варианты.

Поиск в файлах упорядоченных по вероятности: в этих файлах наиболее вероятные элементы находятся в начале, менее вероятные в конце.

Вопрос 22 Алгоритмы поиска в деревьях. Деревья двоичного поиска. Алгоритм вставки и удаления элемента в дерево двоичного поиска. Оценки трудоемкости.

Деревья – это хранилище данных с иерархической структурой. В вершине иерархии находится корневой элемент дерева. В деревьях используют связи элементов как с элементами верхнего уровня (родителями), так и с элементами нижнего уровня (потомками). Связь «родитель-потомок» может организоваться как одни ко многим (1:М), а связь «потомок-родитель» организовывается как один к одному. Т.к. дерево имеет иерархическую структуру, то оно разделяется на уровни (0÷n). Номер уровня показывает количество ссылок до нужного элемента. Количество уровней – это высота дерева. Деревья могут различаться количеством связей.

Д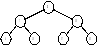 воичное дерево – это дерево, у которого каждый узел имеет не более двух наследников. Вершину дерева называют его корнем, узлы, у которых отсутствуют оба наследника, называются листьями. Высота дерева – это длина наидлиннейшего из путей от корня к листьям. У двоичного дерева количество связей «родитель-потомок» – 2, а у каждого элемента не более 3 связей.

Явное использование структуры данных в виде бинарного дерева позволяет эффективно производить операции не только поиска, но и вставки новых элементов, а также удаления. В структуре дерева каждый элемент имеет кроме ключа data три связи: left – указатель на левое поддерево, right – указатель на правое поддерево и parent – указатель на родителя. Пустой указатель NULL соответствует пустому значению указателя, в конечном узле – листе – оба указателя равны NULL.

Чтобы найти в дереве какое-то значение, мы стартуем из корня и движемся вниз. Например, для поиска числа 16, мы замечаем, что 1620, и потому идем влево. При втором сравнении имеем 167, так что мы движемся вправо. Третья попытка успешна – мы находим элемент с ключом, равным 16. Каждое сравнение вдвое уменьшает количество оставшихся элементов. В этом отношении алгоритм похож на двоичный поиск в массиве. Однако, все это верно только в случаях, когда наше дерево сбалансировано.

Вставка элемента в дерево происходит аналогично поиску. Необходимо найти элемент, к которому производить добавление нового. После того, как такой элемент найден в зависимости от того, больше добавляемый элемент или найденный, элемент вставляется либо как правый, либо как левый потомок. Проблема удаления вершины из двоичного дерева несколько сложнее. Необходимо рассмотреть 3 случая: удаляемая вершина является листом (нет потомков), у удаляемой вершины есть только один потомок, удаляемая вершина имеет двух потомков. В первом случае нет никаких проблем – вершина удаляется из дерева, а ссылка на эту вершину у родителя заменяется на NULL. Во втором случае ссылка у родителя на удаляемую вершину заменяется на ссылку на потомка у удаляемого элемента, после чего требуемый элемент удаляется. В случае номер три все усложняется. Удаляемый элемент необходимо заменить на минимальный элемент из правого поддерева (т.е. минимальный из максимальных). При замене получается, что замещающий элемент тоже удаляется из своего первоначального положения, но его удаление может происходить только по правилу 1 или 2.

Время работы алгоритмов в случае полного двоичного дерева: O (log N). Если считать все двоичные деревья равновероятными, то средняя сложность работы будет O( )!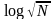

Вопрос 23 Основные информационные характеристики дискретных источников сообщений и каналов. Дискретный источник – источник сообщений, который может в каждый момент времени случайным образом принять одно из конечного множества возможных состояний. Совокупность знаков u₁, u₂,:,u_i,…,u_N соответствующих всем N возможным состояниям источника называют его алфавитом, а количество состояний N – объемом алфавита. Под элементарным дискретным сообщением будем понимать символ u_i выдаваемое источником. Источник определяется дискретным ансамблем U – полной совокупностью состояний с вероятностями их появления, составляющими в сумме 1:

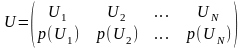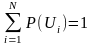, , где 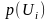- это вероятность выбора источником состояния U_i.

Количество информации: H (U) = log N. Рассматриваемая мера количества информации может иметь лишь ограниченное применение, поскольку предполагает равную вероятность выбора источником любого из возможных его состояний. Когда вероятности различных состояний источника не одинаковы степень неопределенности конкретного состояния зависит не только от объема алфавита источника, но и от вероятности этого состояния. В такой ситуации количество информации, содержащееся в одном дискретном сообщении u_k целесообразно определить как функцию вероятности появления этого сообщения P(u_k) и характеризовать величиной: 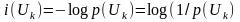Знак минус необходим для того, чтобы количество информации было неотрицательным. Определенное таким образом количество информации определяет только одно случайное сообщение u_k, но не весь ансамбль сообщений.

Для информационной характеристики всего ансамбля используется математическое ожидание количества информации или энтропию: 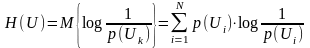Т.о., энтропия источника представляет собой среднее количество информации, содержащейся в одном сообщении источника. Чем больше значение энтропии источника, тем больше степень неожиданности выдаваемых им сообщений в среднем, т.е. тем более неопределенным является ожидаемое сообщение. Свойства энтропии: 1) Энтропия любого дискретного ансамбля неотрицательна: H(U)≥0 Равенство 0 возможно лишь в том случае, когда источник с единичной достоверностью интегрирует единственное сообщение; 2) Пусть N – объем алфавита дискретного источника, тогда H(U)≤logN , причем равенство имеет место лишь в том случае, когда все сообщения ансамбля равновероятны. 3) Энтропия объединения нескольких статистически независимых источников сообщений равна сумме энтропий исходных источников

Условная энтропии H(U/Z), описывающей среднее количество информации, содержащейся в сообщении ансамбля U, при условии, что сообщение ансамбля известно.

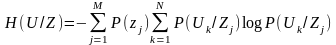
Энтропия дискретного источника максимальна в том случае, когда выполняется два условия: 1) все сообщения источника независимы; 2) все сообщения источника равновероятны. Невыполнение любого из этих требований уменьшает энтропию источника и является причиной избыточности.

Избыточностью источника дискретных сообщений с энтропией H_u и объемом алфавита N называется величина: 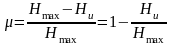, где H_max – максимально возможное значение энтропии при данном объеме алфавита. Оно достигается при выполнении двух предыдущих условий: H_max = log N.

Избыточность показывает, какая доля максимально возможной при заданном объеме алфавита энтропии не используется источником.

При генерировании источником последовательно сообщений существует ещё один фактор, влияющий на величину энтропии - наличие или отсутствие у источника памяти. Источник дискретных сообщений называется источником с памятью, если вероятность выдачи им очередного элемента сообщения u_k зависит от того, какой элемент сообщения был выдан ранее. Иначе говоря, сообщения источника с памятью являются зависимыми. Стационарный источник независимых сообщений называется источником без памяти.

Обычно источники передают сообщения, с некоторой скоростью, затрачивая в среднем время Т на передачу одного сообщения. Производительность источника H’(U) это суммарная энтропия сообщений переданных за единицу времени:

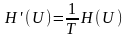
В еличина i’(U,Z) называется скоростью передачи информации от U к Z или наоборот. H'(U) производительность источника передаваемого сигнала U, а H'(Z) производительность канала, т.е. полная собственная информация в принятом сигнале за единицу времени. Величина H’(U/Z) представляет собой потерю информации или ненадежность канала в единицу времени, а H’(Z/U) скорость создания ложной, посторонней информации в канале не имеющей отношение к U и обусловленная присутствующими в канале помехами.

Пропускная способность дискретного канала – максимальное количество переданной информации, взятое по всевозможным источникам входного сигнала, характеризует сам канал, и называется пропускной способностью канала в расчете на один символ:

Обычно определяют пропускную способность в расчете на единицу времени и называют ее просто пропускной способностью канала.