
- •Вопрос 1 Непрерывность действительных функций одного и многих действительных переменных. Свойства непрерывных функций.
- •Вопрос 2 Числовой ряд. Сходящиеся ряды и их простейшие свойства. Функциональные ряды. Равномерно сходящиеся ряды. Степенные ряды. Область и радиус сходимости степенного ряда.
- •Вопрос 4 Матрицы над кольцом и операции над ними. Определители матриц и их свойства. Ранг матрицы над полем. Обратная матрица и способы ее вычисления.
- •Вопрос 5 Векторные пространства над полем. Линейно зависимые и независимые системы векторов. Подпространства векторного пространства, операции над ними. Свойства конечномерных векторных пространств.
- •Вопрос 6 Кольцо многочленов над кольцом с единицей. Делимость многочленов с остатком. Значение многочлена, его корень.
- •Вопрос 8 Евклидово (унитарное) пространство и его свойства. Ортогонализация системы векторов. Существование ортонормированного базиса. Ортогональное дополнение подпространства.
- •Вопрос 9 Кольца вычетов. Малая теорема Ферма. Сравнения первой степени. Китайская теорема об остатках.
- •Вопрос 10 Вероятностное пространство. Аксиомы теории вероятностей. Классическое определение вероятности.
- •Вопрос 11 Случайные величины, функции распределения, их свойства. Абсолютно непрерывные и дискретные распределения. Типовые распределения: биномиальное, пуассоновское, нормальное.
- •Вопрос 12 Условные вероятности. Независимость событий. Формула полной вероятности. Формулы Байеса. Независимые случайные величины.
- •Вопрос 13 Математическое ожидание случайной величины и его свойства. Примеры. Дисперсия случайной величины и ее свойства. Вычисление математических ожиданий и дисперсий типовых распределений.
- •Вопрос 15 Центральная предельная теорема для независимых одинаково распределенных случайных величин.
- •Вопрос 16 Основные понятия математической статистики и т.Д..
- •Вопрос 18 Критерии согласия. Критерий согласия Пирсона (критерий 2).
- •Вопрос 19 Алгоритмы сортировки. Сортировки сравнениями: пузырьковая сортировка и сортировка вставками. Оценки трудоемкости.
- •Вопрос 21 Цифровая сортировка как пример сортировки подсчетом. Бинарный и интерполяционный поиск. Оценки трудоемкости.
- •Вопрос 22 Алгоритмы поиска в деревьях. Деревья двоичного поиска. Алгоритм вставки и удаления элемента в дерево двоичного поиска. Оценки трудоемкости.
- •Вопрос 24 Теорема Шеннона для канала без шума и ее практическое значение.
- •Вопрос 25. Теорема Шеннона для канала с шумом и ее практическое значение.
- •Вопрос 26 Классификация помехоустойчивых кодов и принципы их построения.
- •Вопрос 27 Угрозы безопасности информации. Классификация и модель угроз безопасности. Угрозы конфиденциальности, целостности, доступности, раскрытия параметров ас.
- •Вопрос 28 Понятие политики безопасности. Формирование и структура политики иб. Дискреционная политика безопасности. Мандатная политика безопасности.
- •Вопрос 29 Основные положения руководящих документов фстэк в области зи.
- •Вопрос 30 Определение и классификация нарушителя. Модель нарушителя. Модель нарушителя в соответствии с рд фстэк.
- •Вопрос 32 Стандарт по обеспечению информационной безопасности гост р исо/мэк 17799. Практические правила управления иб. Отправная точка для внедрения иб.
- •Вопрос 33 Стандарт по обеспечению информационной безопасности гост р исо/мэк 27001. Система менеджмента информационной безопасности.
- •Вопрос 34 Формальные модели безопасности. Модель Белла-Лападула как основа построения систем мандатного разграничения доступа. Основные положения модели.
- •Вопрос 35 Методы и средства ограничения и управления доступом. Пас управления доступом. Типовая структура и типовые функции пас управления доступом.
- •Вопрос 36 Методы и средства привязки программного обеспечения к аппаратному окружению и физическим носителям.
- •Вопрос 37. Защита программ от исследования. Методы и средства защиты.
- •Вопрос 38. Защита от разрушающих программных воздействий (рпв). Методы и средства защиты от разрушающих программных воздействий. Изолированная программная среда.
- •Вопрос 39 Информативные сигналы и их источники. Побочные электромагнитные излучения и наводки. Структура, классификация и основные характеристики технических каналов утечки информации.
- •Вопрос 40 Скрытие речевой информации в каналах связи. Энергетическое скрытие акустических информативных сигналов.
- •Вопрос 42 Криптосистемы с открытым ключом. Понятие сертификата. Криптосистема rsa. Выбор параметров.
- •Вопрос 43 Криптографические хэш-функции. Стандарт гост р 34.11.
- •8.3 Этап
- •Вопрос 44 Цифровая подпись. Схемы цифровой подписи. Стандарт гост р 34.10.
- •45 Блочные шифры. Режимы блочных шифров. Гост 28147.
- •46 Протоколы открытого ключевого обмена. Диффи-Хеллман
- •Вопрос 47. Классификация ключей по типам алгоритмов, их функциям, уровням и криптопериоду.
- •Вопрос 48 Основные механизмы безопасности операционных систем (ос): средства и методы аутентификации в ос, модели разграничения доступа, организация и использование средств протоколирования.
- •Вопрос 49. Администрирование ос: основные задачи и принципы сопровождения системного по, управления безопасности ос.
- •Вопрос 50 Классификация сетевых атак. Классификация средств сетевой защиты
- •Вопрос 51. Основные принципы обеспечения безопасности в Internet.
- •Вопрос 53 Защита информации ограниченного доступа: коммерческой тайны.
- •Вопрос 54 Защита государственной тайны.
- •Вопрос 55 Защита информации ограниченного доступа: персональных данных.
- •Вопрос 56 Лицензирование деятельности в области защиты информации.
- •Вопрос 57. Сертификация средств защиты информации.
- •Вопрос 58. Аттестация объектов информатизации.
Вопрос 1 Непрерывность действительных функций одного и многих действительных переменных. Свойства непрерывных функций.
Функция
y=f(x)
называется непрерывной
в точке
х0,
если
эта функция определена в какой-нибудь
окрестности
точки х0
и
если
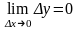 ,
т.е. если бесконечно малому приращению
аргумента соответствует бесконечно
малое приращение функции.
,
т.е. если бесконечно малому приращению
аргумента соответствует бесконечно
малое приращение функции.
Функция называется непрерывной в интервале, если она непрерывна в каждой его точке. Для левого конца интервала приращению ∆x следует придавать только положительные значения, а для правого –отрицательные.
Функция
z=f(x,у) называется непрерывной
в точке
(х0,у0),
если она определена в некоторой
окрестности этой точки и если бесконечно
малым приращениям х и y
соответствует бесконечно малое приращение
z,
т.е.
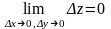 .
.
Непрерывные функции двух независимых переменных обладают теми же основными свойствами, что и непрерывные функции одной независимой переменной. Все основные элементарные функции непрерывны в тех интервалах, в которых они определены.
Теорема 1: сумма конечного числа функций, непрерывных в некоторой точке, является функцией, непрерывной в той же точке
Теорема 2: произведение конечного числа функций, непрерывных в некоторой точке, является функцией, непрерывной в той же точке.
Теорема 3: частное 2 функций, непрерывных в некоторой точке, является функцией, непрерывной в той же точке, если знаменатель не обращается в ней в 0.
Теорема 4: сложная функция, составленная из конечного числа непрерывных функций, непрерывна.
Теорема 5: функция, обратная к монотонной и непрерывной функции, непрерывна.
Теорема 6: функция, непрерывная в замкнутом интервале, хотя бы в одной точке интервала принимает наибольшее значение и хотя бы в одной – наименьшее.
Теорема 7: функция, непрерывная в замкнутом интервале и принимающая на концах этого интервала значения разных знаков, хотя бы один раз обращается в нуль внутри интервала.
Теорему 8: функция, непрерывная в замкнутом интервале, принимает внутри интервала хотя бы один раз любое значение, заключенное между ее значениями на концах интервала.
Вопрос 2 Числовой ряд. Сходящиеся ряды и их простейшие свойства. Функциональные ряды. Равномерно сходящиеся ряды. Степенные ряды. Область и радиус сходимости степенного ряда.
Задана
бесконечная последовательность любых
чисел: U1,U2,…,Un.
Тогда выражение
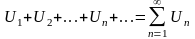 называется числовым
рядом, а
U1,U2,…,Un
называются членами
ряда. Сумма
конечного числа n
первых членов ряда U1+U2+…+Un=Sn
называется n-ой
частичной суммой ряда.
называется числовым
рядом, а
U1,U2,…,Un
называются членами
ряда. Сумма
конечного числа n
первых членов ряда U1+U2+…+Un=Sn
называется n-ой
частичной суммой ряда.
Если
существует конечный предел, то ряд
сходится:
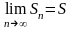
Если
предела не существует, то ряд расходится:
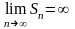
Свойства
рядов:
1. произведение
ряда на число есть ряд:
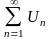 -
ряд, С – число,
-
ряд, С – число,
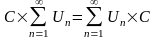
2. сумма
двух или более рядов есть ряд:
-
ряд,
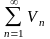 -
ряд,
-
ряд,
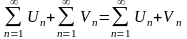
Теорема: если сходится ряд, то сходится и его остаток. Справедливо и обратное. Если ряд расходится, то расходится и его остаток.
Необходимый признак сходимости ряда (условие, при невыполнении которого ряд расходится): если ряд сходится, то его n-ый член стремится к 0. Обратное не верно!
Достаточный
признак расходимости ряда:
если n-ый
член ряда не стремится к 0, то ряд
расходится Функциональные
ряды –
ряды, членами которых являются функции:
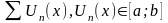
Пусть
дан функциональный ряд:
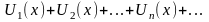 .
Совокупность тех значений х, при которых
ряд сходится, называется областью
сходимости
этого ряда. Очевидно, что в области
сходимости ряда его сумма является
некоторой функций от х – S(x):
.
Совокупность тех значений х, при которых
ряд сходится, называется областью
сходимости
этого ряда. Очевидно, что в области
сходимости ряда его сумма является
некоторой функций от х – S(x):
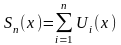 .
.
Свойства равномерно сходящихся рядов:
1. если члены ряда непрерывны, то его сумма есть непрерывная функция. Если сумма ряда на каком-либо промежутке [a;b] разрывна, то ряд не можарируем на этом отрезке;
2. если ряд сходится равномерно, то его можно почленно интегрировать;
3. если ряд сходится равномерно, то его можно почленно дифференцировать, если получающийся при этом ряд сходится равномерно.
Степенным
рядом
называется функциональный ряд вида
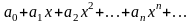 ,
где аi –
Const
или коэффициенты ряда.
,
где аi –
Const
или коэффициенты ряда.
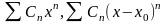
Областью сходимости степенного ряда всегда является некоторый интервал, который может вырождаться в точку. Это доказывает теорема Абеля: если степенной ряд сходится при некотором значении х0, где х0≠0, то он абсолютно сходится при всяком значении х, для которого |х|<|х0|; если ряд расходится при некотором х0≠0, то он расходится при всяком значении х, для которого |х|<|х0|.
Теорема Абеля позволяет судить о расположении точек сходимости и расходимости степенного ряда. Если х0 – точка сходимости, то (–|х0|;|х0|) заполнен точками абсолютной сходимости. Если х0 – точка расходимости, то вся бесконечность полупрямых влево и вправо заполнена точками расходимости.
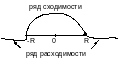
Существует такое число R, что при |х|<R существуют точки абсолютной сходимости, а при |х|>R – точки расходимости. Интервал сходимости степенного ряда называют такой (-R;R), что для всякого х, лежащего внутри этого интервала, ряд сходится абсолютно; а для точек, лежащих вне его, ряд расходится. Число R называется радиусом сходимости ряда на концах(-R;R).
Вопрос 3 Первообразная
и неопределенный интеграл. Интеграл
Римана (определенный интеграл) и его
свойства, классы интегрируемых функций.
Функция F(x)
называется первообразной от функции
f(x)
на отрезке [a;b],
если во всех точках этого отрезка
выполняется равенство: F(x)=f(x),
dF(x)=f(x)dx.
Свойства
первообразных и неопределённого
интеграла 1.
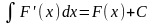 .
.
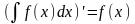 2.
Постоянный
множитель можно вынести за знак
интеграла.
2.
Постоянный
множитель можно вынести за знак
интеграла.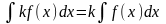 ,
где k -
сonst. 3.
Интеграл от
суммы равен сумме интегралов:
,
где k -
сonst. 3.
Интеграл от
суммы равен сумме интегралов:
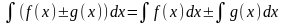 .
.
4.
Формула замены
под знаком интеграла.
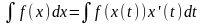 .
5. первообразная
не зависит от вида переменной
интегрирования.
.
5. первообразная
не зависит от вида переменной
интегрирования.
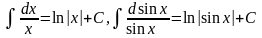
Пусть
f(x) -
функция, заданная на объединении
интервалов вещественной оси. Набор всех
первообразных для f(x)
называется неопределённым
интегралом
от f(x)
и обозначается
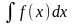 .
.
Определенный интеграл – одно из основных понятие мат.анализа. к вычислению определенного интеграла сводится вычисление площадей и т.д.
Теорема
существования интеграла (Теорема Коши):
если подынтегральная функция f(x)
непрерывна (кусочно-непрерывна) на [a;b]
=> определенный интеграл существует
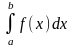 .
Свойства: 1)
.
Свойства: 1)
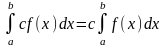 ;
2)
;
2)
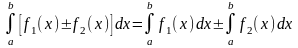 ;
3)
;
3)
 ;
4) пусть
;
4) пусть
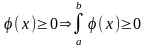 ;
5) пусть
;
5) пусть
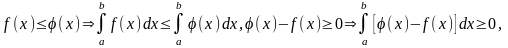
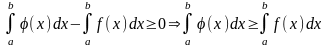 ;
6) среднее
значение функции.
y=f(x)
непрерывна на [a;b].
;
6) среднее
значение функции.
y=f(x)
непрерывна на [a;b].
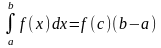 ,
где c
– точка на [a;b].
,
где c
– точка на [a;b].
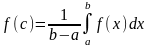 -
среднее значение функции; 8)
разбиение интеграла по промежуткам.
-
среднее значение функции; 8)
разбиение интеграла по промежуткам.
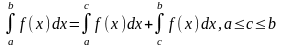 9)
условие
9)
условие
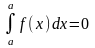 ;
10)
;
10)
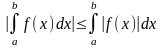 .
.
Приложения
определенного интеграла. 1)
Вычисление площади плоской фигуры
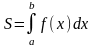 .
.
2)
Вычисление длины дуги кривой. За длину
дуги кривой мы принимаем
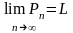 .
.
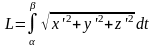 -
3) Объем
тел, объем цилиндра,
-
3) Объем
тел, объем цилиндра,
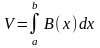 .
4)
Объем тел вращения.
.
4)
Объем тел вращения.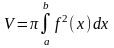 .
.
