4.4 Расчет коэффициентов обратных модальных связей

Дальнейшее решение поставленной задачи синтеза системы модального управления сводится к совместному решению системы четырех уравнений (4.5), (4.12) относительно неизвестных

То есть имеем систему уравнений:

Для краткости последующих записей и удобства решения введем обозначения

; ; ; (2.13)

; ; ; (2.14)

; ; (2.15)

причем

(2.16)

Тогда система указанных уравнений принимает вид

(2.17)

Поскольку в системе (2.17) число уравнений превышает число неизвестных, то необходимо установить условие ее совместности. Для этого из первых трех уравнений определяем

; ; ; (2.18)

Подставляя (2.18) в последнее уравнение системы (2.17) и учитывая (2.16), получаем следующее уравнение совместности

,

которое после подстановки принятых обозначений (2.15),(2.16) приводится к виду:

(2.19)

Неполное кубическое уравнение (2.19) решим численно. При этом в дальнейшем будем использовать лишь наименьший положительный корень уравнения ,приближенное значение которого определяется по формуле:

(2.20)

8,766687

где = 2,049, = 2,397 (согласно рисунку 1.1)

Вычисленное согласно (2.20) значение может использоваться лишь в качестве первого (грубого) решения при численных способах решения уравнения (2.19).

Найдем и проверим точное значение корня, которое в силу особенностей уравнения (2.19) всегда будет несколько больше, чем его приближенное значение (2.20).

Определим f ₁ и f₂:

f₁ =

f₂ =

=> f₁ ≠ f_2, f₁>f₂

Определим точное значение Ω₀:

Предположим, что Ω₀ = 1,017 · 8,766687 = 8,854354

Тогда:

f₁ =

тогда f₂ =

Проверим погрешность измерений:

=> принимаем Ω₀ = 8,854354

Определив точное значение , оценим ожидаемое время регулирования , которое в соответствии с рисунком 1.1 вычислим по формуле

(2.21)

=4,37 /8,854354= 0,493543 с

Величина не превышает указанного в задании значения (0,7 c):

= 0,493543 c < 0,7 c

На основании (2.14) вычисляем величины :

= -9,070423

= 0,021139

= 1,074538

На основании (2.18) вычисляем величины :

= -10,070423

= 0,021139 + 9,070423= 9,091562

= 1,074538 + 9,070423 = 10,144961

Исходя из (2.13) имеем

; ; (2.22)

Теперь, как было отмечено в п.4.2 , достаточно задаться одним из коэффициентов , чтобы согласно (2.22) однозначно определить все остальные.

Определим в начале коэффициент . Для этого из табл.4 на основании условия выберем тип тахогенератора и соответствующее ему значение .

Таблица 4.1 - Параметры тахогенераторов по типам

Тип тахогенератора	ТД-201	ТГ-1	ТД-102	ТД-103	ТГ-2	ТД-110
Максимальная частота вращения , об./ мин	1000	1100	1500	1500	2400	3000
Коэффициент передачи , В / (рад/c)	1,3	0,07	0,5	1,0	0,2	0,48

Имеем согласно заданию =750 об/мин.

Нашим условиям подходит тахогенератор типа ТД-201 , у которого = 1,3

Теперь на основании (2.22) последовательно вычисляем значения :

36,985386

= -20,528909

0,370715

Выполним проверку полученных результатов. Для этого согласно (2.4) вычислим значения и проверим выполнение условий

, ,

(погрешность между левой и правой частями этих равенств не должна превышать 1%)

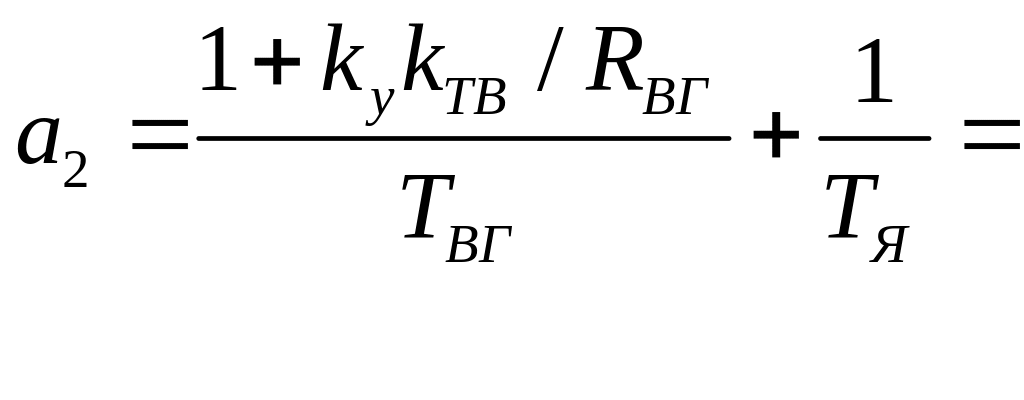18,142571

187,9238030

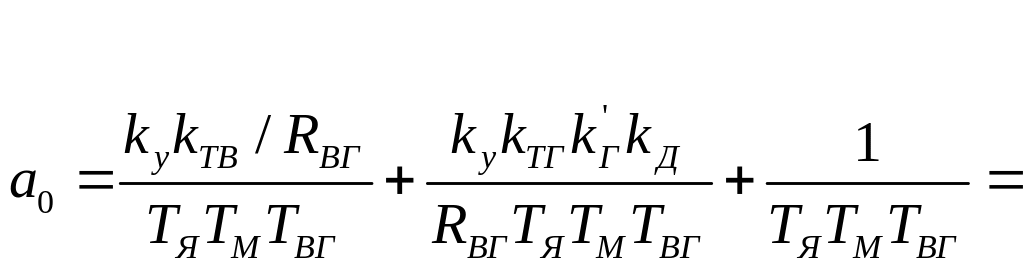694,177669

Проверим выполнение условия для a₂: = 2,049 ∙ 8,854354 = 17,493122

Также проверим значение : = 2,397 ∙8,854354 = 141,999690

И, наконец, значение : = 694,177669

Теперь согласно (2.11) вычислим значение , которое должно отличаться от указанного в задании тоже не более 1%

= 0,006695 0,01 (по условию)