Дискретные случайные величины

Случайные величины обозначаются заглавными буквами X, Y, Z. Запись X=x означает, что случайная величина X приняла значение x, P(X=x) означает вероятность того, что случайная величина X приняла значение x.

Законом распределения дискретной случайной величины называют соответствие между возможными значениями и их вероятностями. Его можно задать таблично, аналитически (в виде формулы) и графически.

Табличный способ (или ряд распределения)

X	x1	x2	x3	…	xn
P	p1	p2	p3	…	pn

В верхней строке приведены значения случайной величины, в нижней – вероятности каждого ее значения.

Так как в одном испытании случайная величина принимает одно и только одно возможное значение, то события X=x₁,… X=x_n – образуют полную группу, значит, .

Графический ряд распределения

(многоугольник или полигон распределения)

В прямоугольной системе координат строятся точки 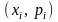и затем соединяются.

Пример. В денежной лотерее выпущено 100 билетов. Разыгрывается один выигрыш в 50 руб. и 10 выигрышей по 1руб. Найти закон распределения случайной величины X – стоимости возможного выигрыша для владельца одного билета.

Табличный способ

X	50	1	0
P	=0.01	=0.1	1- - =0.89

Числовые характеристики дискретной случайной величины

Математическое ожидание

Определение. Математическим ожиданием M(X) случайной величины X называется сумма произведений всех ее возможных значений на соответствующие вероятности, т.е. .

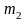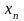
Выясним смысл этой формулы. Пусть случайная величина X принимает значение раз, раз,……. раз, причем .

Вычислим среднее арифметическое всех значений случайной величины

.

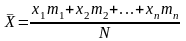Но 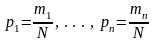- вероятности появления соответствующих значений случайной величины. Значит математическое ожидание равно среднему значению случайной величины.

Пример.

X	3	5	2
P	0,1	0,6	0,3

.

Свойства математического ожидания.

1. Если С – постоянная, то .

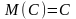2. .

3. .

4. Если X и Y – независимые события, то .

Дисперсия дискретной случайной величины

Рассмотрим две случайные величины.

X	- 0,01	0,01
p	0, 5	0, 5

Y	- 50	50
p	0, 5	0, 5

Ясно, что Если эти случайные величины представляют собой отклонение снаряда от цели, то первый же снаряд в первом случае поразит цель, а во втором случае она не будет поражена. Таким образом, математическое ожидание не всегда дает необходимую информацию. Необходимо как то учесть разброс значений. Для этого и вводится понятие дисперсии.

Определение. Дисперсией (рассеянием) случайной величины называется математическое ожидание квадратов ее отклонений:

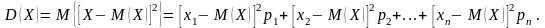Геометрический смысл дисперсии – это среднее арифметическое квадратов отклонений случайной величины от ее среднего значения. Именно квадраты отклонений дают объективную характеристику рассеяния случайной величины. Сами отклонения могут принимать как отрицательные значения, так и положительные, что может дать ложное представление о разбросе данных. Из приведенных таблиц видно, что сами отклонения в сумме дают нулевое рассеяние, что неверно, особенно во втором случае.

Свойства дисперсий.

1. Дисперсия постоянной величины равна нулю.

2.

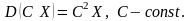
3. Дисперсия суммы двух независимых случайных величин равна сумме дисперсий этих величин.

4. Дисперсия числа появления события А в n независимых испытаниях, в каждом из которых вероятность появления события p постоянна, равна произведению числа испытаний, вероятности появления события и вероятности непоявления события q = 1- p:

Среднее квадратическое отклонение

Определение. Среднее квадратическе отклонение случайной величины X равно квадратному корню от дисперсии:

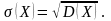
Среднее квадратическое отклонение рассмотренной выше случайной величины равно

Замечание. Дисперсия и среднее квадратическое отклонение так же, как и математическое ожидание, не являются случайными величинами, а имеют постоянное значение.

Пример.

X	1	2	5
P	0,3	0,5	0,2

.

[x₁-M(X)]²=(1 - 2,3)²=1,69;

[x₂-M(X)]²=(2 - 2,3)²=0,09;

[x₃-M(X)]²=(5 - 2,3)²=7,29

[X-M(X)]2	1,69	0,09	7,29
P	0,3	0,5	0,2

.

.