Теория вероятностей.
В окружающем нас мире мы наблюдаем различные события, сталкиваемся с результатами многочисленных опытов и наблюдений. Раздел математики, называемый теорией вероятностей, занимается изучением закономерности в случайных событиях.
Первые работы, в которых зарождались основные понятия теории вероятностей, представляли собой попытки создания теории азартных игр. Это происходило в 16-17 веках в Европе. В это время богатые люди увлекались игрой в карты, в кости и т.п.
Одним из создателей теории вероятности был Блез Паскаль (1623 – 1662). Он пришел к своим выводам, решая задачи о стратегии игр в кости. Паскаль писал о теории вероятностей:
«Это учение, объединяющее точность математических доказательств с неопределенностью случая и примиряющее эти казалось бы противоречивые элементы, с полным правом может претендовать на титул математики случайного».
Почти за 100 лет до Паскаля итальянец Дж.Кардано (математик, врач) написал книгу, которая называлась «Книга об игре в кости».
Сочинения по этому вопросу есть и у Г.Галилея.
Первое теоретическое обоснование накопленным ранее знаниям дал Яков Бернулли (1654 – 1703). Он доказал «Закон больших чисел», о котором мы будем говорить позже.
Прежде, чем переходить к изучению теории вероятностей, рассмотрим раздел математики, который называется комбинаторика.
Основные формулы комбинаторики.
Определение 1. Соединением называют подчиненные определенным условиям комбинации, которые можно составить из элементов заданного конечного множества.
Различают три основных вида соединений: перестановки, размещения и сочетания.
Определение 2. Перестановками из n элементов называются соединения, содержащие все n элементов и отличающиеся между собой лишь порядком элементов. Число перестановок из n элементов определяется формулой:
Задача. Сколько трехзначных чисел можно составить из цифр 1; 2; 3, если каждая цифра входит в число один раз.
Решение:
Проверим это: 123; 132; 213;
231; 321; 312. Других чисел нет.
Замечание. Ранее предполагалось,
что все n элементов
различны. Если среди n
элементов имеется
элемент одного вида,
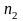элемента другого вида, и так далее, то
Определение 3. Размещениями из
n элементов по m
(
)
называются соединения, в каждое из
которых входит m
элементов, взятых из данных n,
отличающиеся друг от друга либо самими
элементами, либо порядком их расположения.
Число размещений из n элементов по m определяется формулой
Задача. Сколько сигналов можно составить из трех флажков белого, синего и красного цветов, взятых по два?
Решение:
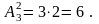Проверим: б с, б к, с б, с к, к б, к с.
Определение 4. Сочетаниями из n элементов по m ( ) называются соединения, в каждое из которых входит m элементов, взятых из данных n, отличающиеся друг от друга хотя бы одним элементом.
Число сочетаний из n элементов по m определяется формулой
Из формулы следует
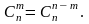
Задача. Сколькими способами из 8 человек можно выбрать комиссию из 5 человек?
Решение: Поскольку создаваемые комиссии должны отличаться от других хотя бы одним членом, имеем
Задачи для домашней работы
Сколькими способами 6 человек могут встать в очередь?
В забеге участвуют 5 студентов. Сколькими способами могут распределиться два первых места?
Группе необходимо сдать 5 экзаменов в течение 20 дней. Сколькими способами можно составить расписание экзаменов?