2.5. Отношение порядка

Определение 2.19. Бинарное отношение  называется отношением строгого порядка, если оно антирефлексивно и транзитивно.

Определение 2.20. Бинарное отношение  называется отношением нестрогого порядка (частичного порядка), если оно рефлексивно, транзитивно и антисимметрично.

Отношение строгого и нестрогого порядка называется отношением порядка.

Определение 2.21. Бинарное отношение порядка называется совершенным, если оно является связным.

Определение 2.22. Множество, для которого определено отношение порядка, называется множеством, упорядоченным этим отношением. Если порядок, определенный на множестве, является совершенным, то множество называется линейно упорядоченным или полностью упорядоченным множеством. Если порядок не является совершенным, то множество называется частично упорядоченным.

Отношение, обратное отношению частичного порядка будет, очевидно, отношением частичного порядка.

Пример 2.23.

1) Пусть X – конечное множество, X = {1, 2, 3} и  = {(1, 1), (1, 2), (1, 3), (2, 2), (2, 3), (3, 3)}. Отношение  есть отношение частичного порядка.

2) Пусть X – конечное множество, X = {1, 2, 3} и  = {(1, 2), (1, 3), (2, 3)}. Отношение  есть отношение строгого порядка.

3) Отношение А  В на множестве подмножеств некоторого множества U есть отношение частичного порядка.

4) Отношение делимости (обозначение – « ») на множестве натуральных чисел есть отношение частичного порядка.

5) Отношение сравнения по величине (обозначение – « »).

Отношения порядка будем обозначать символом « », если это не будет приводить к недоразумениям.

Пример 2.24.

1. - линейно упорядоченное множество.

2. - линейно упорядоченное множество.

3. Пусть A={1,2,3}. Множество всех его подмножеств не является вполне упорядоченным.

Определение 2.23. Пусть - упорядоченное множество.

1. Если (a,b) , то этот факт будем записывать в виде или , и говорить «a меньше либо равно b», «b больше либо равно a» (в смысле отношения порядка ). Если или и a ≠ b, то будем писать a < b или b > a и говорить «a меньше b», «b больше a».

2. Элемент называется минимальным (максимальным), если в A нет элементов, меньших (больших) элемента a.

3. Элемент называется наименьшим (наибольшим) элементом множества A, если этот элемент меньше (больше) любого другого элемента из A.

Пример 2.25. Пусть A={1,2,3}.

1. B(A)={,{1},{2},{3},{1,2},{1,3},{2,3},A}, 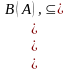– упорядоченное множество, наименьший элемент (он же минимальный) – , наибольший (он же максимальный) – само множество A.

2. B₀(A)=B(A)\{}, – упорядоченное множество, наименьшего элемента нет, минимальные – {1}, {2}, {3}, наибольший (он же максимальный) – A.

3. B₁(A)=B(A)\{A}, – упорядоченное множество, наибольшего элемента нет, максимальные – {1,2}, {2,3}, {1,3}, наименьший (он же минимальный) – .

4. B₂(A)=B(A)\{ , A}, – упорядоченное множество, наибольшего и наименьшего элементов нет, максимальные – {1,2}, {2,3}, {1,3}, минимальные – {1}, {2}, {3}.

5. – упорядоченное множество, наибольшего и максимальных элементов нет, наименьший (он же минимальный) – 1.

6. – упорядоченное множество, наибольшего и максимальных элементов нет, наименьший (он же минимальный) – 1.

7. – упорядоченное множество, наибольшего, наименьшего и максимальных элементов нет, минимальные – все простые числа.

Теорема 2.2.

1. Упорядоченное множество имеет не более одного наименьшего и не более одного наибольшего элемента.

2. Наименьший элемент упорядоченного множества является единственным минимальным элементом этого множества.

3. Наибольший элемент упорядоченного множества является единственным максимальным элементом этого множества.

Определение 2.24. Пусть – некоторое упорядоченное множество. Элементы a,b A называются сравнимыми, если или . В противном случае элементы a и b называются несравнимыми.

Определение 2.25. Пусть – некоторое упорядоченное множество. , .

1. a называется нижней границей (верхней границей) множества B, если a меньше (больше) любого элемента из B, отличного от a.

2. a называется точной нижней границей (точной верхней границей) множества B, если a есть нижняя граница (верхняя граница) и a больше (меньше) любой другой нижней (верхней) границы множества B.

3. A называется решеткой, если любая пара элементов из A имеет точную верхнюю границу и точную нижнюю границу.

Пример 2.26.

1. Пусть A={1,2,3,4,5}.

1. не является решеткой.

2. Пусть  =  {(1,3), (2,3), (1,4), (2,4), (3,5), (4,5), (1,5), (2,5)}, тогда не является решеткой.

2. Пусть A={1,2,3}. Тогда – решетка.

3. – решетка.